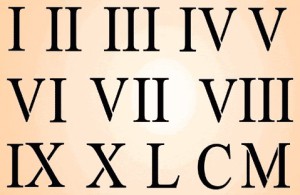Чем история римских и арабских цифр похожи
Интересный факт!
Интересно, любопытно, удивительно
Римские и арабские цифры. Происхождение и написание. Видео.
Posted by: admin | on Ноябрь 25, 2013
Дорогие друзья!
Сегодня нас нисколько не удивляют встречающиеся в текстах римские и арабские цифры (Пётр I, 2013 год). Они мирно соседствуют рядом, стали для всх привычными. Но давайте поговорим про их происхождение и написание (видео).
Римские цифры.
Римские цифры возникли ещё за полвека до наступления новой эры, и в основу их графического написания было положено изображение пальцев руки и самой ладони, поскольку именно руки были первым инструментом для счёта.
Римские числа именно так и записываются: если меньшая по значению цифра находится слева от большей – она вычитается из неё IX (то есть,10-1=9), а если она стоит справа от большей, то прибавляется XI (10 + 1 =11).
Для этого нужно знать не только обозначение единицы и десятка, а также сотен и тысяч.
А чтобы не забыть обозначения римских цифр, используется следующая памятка:
М — Мы D — дарим С — сочные L — лимоны, Х — хватит V — всем I — их.
Дорогие друзья, с наступающим Вас ММXIV годом!
Арабские цифры.
Арабы переняли те цифры, что называются теперь «арабскими» у индусов, а европейцы уже заимствовали эти цифровые символы у арабов в конце средневековья.
Само слово «цифра» пришло к нам также из арабского языка.
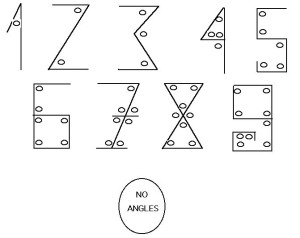
Существует одна из гипотез, что некий арабский математик древности предложил связать количество углов написанной цифры с её числовым значением.
Очертания всех арабских цифр состояли из отрезков, при соединении дававших определённое количество углов.
Не имеет углов только цифра «ноль» (придуманная гораздо позже остальных цифр), поэтому она единственная изображается в виде овала.
Итак, арабские цифры выглядят следующим образом (напоминают написание индекса на конвертах):
0 — цифра не имеет углов;
1 — имеет один угол;
2 — имеет два угла;
3 — имеет три угла;
4 — содержит четыре угла, два из которых прямые;
5 — имеет пять прямых углов;
6 — имеет шесть прямых углов;
7 — имеет семь острых и прямых углов;
8 — имеет восемь прямых углов;
9— имеет девять прямых углов.
Со временем исчезла необходимость каждый раз считать количество углов, чтобы определить обозначаемое цифрой количество; очертания цифр приобрели более округлый вид, и уже много веков весь мир использует их для записи чисел.
Видео.
На этом интересный факт исчерпал себя!
Но завтра найдём что-нибудь более интересное!
С наилучшими пожеланиями здоровья и благоденствия,
Ваш преданный гид по Миру Интересных Фактов,
Римские цифры придумали действительно в Древнем Риме, потому как
думающих людей там было очень много, и более того, наука там
приветствовалась. Что же касаемо, привычных нам арабских цифр, то есть
мнение, что они пришли из южной Индии, при чем эта версия очень
аргументирована, а вот в Европу они пришли при активном содействии этому
великому математику Фибоначчи.
Изобретение цифр – явление относительно позднее! Сегодня весь мир
пользуется изобретением, сделанным в одном месте – в Индии. Индийцы
изобрели современные цифры, изобрели ноль, позволивший экономно и точно
записывать любые числа. От индийцев эти цифры распространились через
Иран к арабам, и затем уже арабы занесли их в Европу. Мы называем их
арабскими цифрами, тогда как в действительности эти цифры индийские.
Первое
достоверное свидетельство о записи нуля относится к 876 г. ; в настенной
надписи из Гвалиора (Индия) имеется число 270. Некоторые исследователи
предполагают, что нуль быль заимствован у греков, которые ввели в
качестве нуля букву «о» в шестидесятеричную систему счисления,
употребляемую ими в астрономии.
Другие, наоборот, считают, что ноль
пришёл в Индию с востока, он был изобретён на границе индийской и
китайской культур. Обнаружены более ранние надписи от 683 и 686 гг. в
нынешних Камбодже и Индонезии, где нуль изображён в виде точки и малого
кружка. Майя использовали ноль в своей двадцатиричной системе счисления
почти на тысячелетие раньше индийцев.
В империи инков Тауантинсуйу
для записи числовой информации использовалась узелковая система кипу,
основанная на позиционной десятиричной системе счисления. Цифры от 1 до 9
обозначались узелками определённого вида, ноль — пропуском узелка в
нужной позиции.
Римские и арабские цифры
Всё многообразие чисел, которому нет конца, в наши дни выражается на письме десятью знаками. С арабскими цифрами знаком каждый детсадовец, в то время как римские цифры покрыты налётом архаичности и используются разве что на циферблатах часов да в исторических документах. Никто не станет спорить, что арабская система куда проще и универсальнее. Как же происходила смена системы счисления, переход с одного начертания на другое?
Римские цифры появились около 500 лет до нашей эры у этрусков, те в свою очередь могли заимствовать их у далёких предков кельтов – ну или у атлантов на худой конец. Эта система чисел широко известна и в наши дни. Римские цифры можно встретить, например, на циферблате часов Спасской башни Московского Кремля и башне Вестминстерского дворца в Лондоне (Биг-Бен), на постаментах памятников и в документах.
Принцип начертания простейших чисел «по римской традиции» объясняется схожестью с рукой человека. 1, 2, 3, 4 – по количеству пальцев. А цифра V напоминает раскрытую ладонь с четырьмя прижатыми друг к другу пальцами. X при помощи воображения превращается в две скрещенные руки – два раза по пять. Крупные числа не обошлись без связи со словами. Сеntum в переводе с латыни – сто, поэтому 100 – это С. Mile – тысяча, так что 1000 – M. Не то чтобы в то время актуально было прописывать миллионы и миллиарды. людям хватало и этого для повседневного использования.
Курьёзно, но арабскую манеру письма чисел придумали вовсе не арабы. На самом деле современными цифрами мы обязаны Индии – именно здесь были придуманы удобные символы для обозначения чисел. Арабское письмо адаптировало систему записи – впервые это сделал средневековый учёный Мухаммед ибн Муса аль-Хорезми, автор «Китаб аль-Джебр ва-ль-Мукабаля», от названия которой произошёл термин «алгебра». Собственно, появился интерес к точным дисциплинам – понадобилась более совершенная числовая система.
Из арабских стран новые цифры попали в Испанию, а оттуда уже распространились по всей Европе. Не сразу, нет, понадобилось не одна «С» лет. По мере ослабления позиций Римской империи арабские цифры всё более часто возникали то тут то там – сначала красовались на привезённых купцами заморских диковинках, а затем обрели самостоятельность и перекочевали на страницы рукописей, заняв своё законное место на текстовых просторах.
Замена систем счисления
Сейчас с высоты нынешней цивилизации мы понимаем, что смена системы счисления была важнейшим шагом в развитии человечества, без которого оказались бы невозможными многие физические, химические и математические расчёты. Но Европа на протяжении нескольких веков активно сопротивлялась нововведениям. Так, математик Герберт, более известный как папа римский Сильвестр Второй, попытался провести числовую реформу в X веке. От гнева инквизиции его не спас даже почётный титул – учёного папу обвинили во всех грехах и уже после его смерти пресерьёзно уверяли, что из гробницы сочится серный дым.
Если бы не итальянский математик Фибоначчи, невероятными усилиями убедивший общественность в универсальности и простоте этой системы счисления, сопротивление продолжалось бы ещё дольше. А так – в XIII веке уже пользовались новым написанием.
На Руси заморскую диковинку тоже встретили с подозрением. Систему счисления посчитали изобретением католической церкви, из чего вытекало, что арабские цифры непременно безбожные. Их удобство консервативно настроенные жители славянских земель оценили по достоинству только во времена Петра Первого.
Замена римских цифр арабскими оказалась для прогрессивного человечества не менее значимым событием, чем изобретение колеса. То, что сегодня является доступным и понятным каждому, когда-то было величайшим прорывом человеческой мысли.
Улица Мира
ЭТНОМИР, Калужская область, Боровский район, деревня Петрово
Улица Мира в ЭТНОМИРе – уникальный проект, сердце этнографического парка. Не хватит и дня, чтобы внимательно осмотреть все дома и павильоны, которые знакомят с архитектурой, культурой, традициями, ремёслами и гостеприимством разных народов мира. Это самая удивительная улица на свете.
Выставочный комплекс представит собой 15 павильонов общей протяжённостью в 1,5 километра. Каждый из павильонов задуман как отражение культуры и традиций разных регионов мира: старинной Европы, загадочного Востока и самобытной Азии, жаркой Африки, солнечных Австралии и Океании и, конечно, стран Нового Света – Северной и Латинской Америки. Многое в ЭТНОМИРе уже построено, но в проектах – ещё больше. ЭТНОМИР растёт и развивается, приезжайте гулять и познавать мир вместе с нами!
История чисел
Автор: admin · 3 мая, 2014
История возникновения чисел очень глубокая и давняя. Сама жизнь привела людей к тому, что стало просто необходимо использовать символы для написания чисел.
Представьте, ведь давным-давно во времена, когда у людей не было цифр и они не умели считать как мы сейчас, у них все-равно возникало огромное количество поводов для счета. Правда, в те времена им не нужно было применять огромные числа. И самый простой вариант счета подсказала природа. Люди использовали пальцы рук, а при больших числах и ног, чтобы посчитать, например, количество голов скота в стаде. Если уж своих пальцев не хватало, звали приятеля, чтобы уже считать на его руках и ногах. Достаточно неудобно было, а вдруг никого рядом не окажется когда срочно нужно посчитать большое количество чего-нибудь?
Потом кто-то придумал делать глиняные кружочки для подсчета. Например, повел пастух с утра большое стадо на пастбище. Подсчитал всех животных с помощью кружков — сколько кружков, столько животных. Вечером привел их домой, опять смотрит, чтобы каждому животному соответствовал один кружок. Ну и подобных вариантов существовало множество, то есть пользовались подручными средствами.
Первое доказательство использования древними людьми счета — это волчья кость, на которой 30 тысяч лет назад сделали зарубки. Притом они набиты не как-нибудь, а сгруппированы по пять.
Древность.
В Древности у разных народов существовали свои способы счета. Например, майа использовали только три обозначения: точку, линию и эллипс и записывали ими любые цифры.
В Древнем Египте около 5000-4000 лет до н.э. использовали такую запись чисел: единица обозначалась палочкой, сотня — пальмовым листом, а сто тысяч — лягушкой (в дельте Нила было очень много лягушек, вот у людей и возникла такая ассоциация: сто тысяч — очень много, как лягушек в Ниле).
А вот наши предки-славяне использовали самую сложную запись чисел. Они их записывали буквами, над которыми ставили специальный значок «титло», чтобы отличить, где написали буквы, а где цифры, и значков у них было аж 27.
А, например, папуасские племена имели только две цифры, один и два, и называли их «урапун» и «окоза» соответственно. А дальнейшие числа называли просто используя эти два. Например три у них — «окоза-урапун», а четыре — «окоза-окоза». Видимо, считать им особо нечего, поэтому больших чисел у них нет. А все, что больше шести-семи они называют «много». А сколько там «много» уже неизвестно!
Клинопись.
Но человечество развивалось, хозяйство увеличивалось, усложнялись и подсчеты. Появилась потребность в записи чисел. Ведь на память невозможно упомнить, сколько в стаде голов скота, сколько мешков пшеницы у тебя лежит, а сколько потратили, сколько посадили и какой собрали урожай. И вот примерно в V веке до нашей эры появились первые цифры.
Говорят, что первые числа изобрели шумеры, народ, живший на территории Южного Междуречья Тигра и Евфрата, современного Ирака примерно в IV-III тысячелетии до н.э. Шумеры, кстати, очень интересный народ. Огромное количество изобретений, известных сейчас, были впервые использованы ими. Например, постельное белье, обожженный кирпич, колесо.
Шумеры изобрели и так называемое клинописное письмо или клинопись. На глиняных табличках рисовались различные символы в виде клиньев. Цивилизация шумеров была очень развита для тех времен. В их города жили торговцы, ремесленники. Для счета применялись сначала глиняные фишки различной формы. Со временем на них стали делать пометки, которые обозначали количество и вид того, что считали. Например, две козы. Но два мешка писали совершенно по-другому. То есть они описывали количество конкретных объектов и не выделяли отдельно цифру.
После шумеров на этих землях обосновались вавилоняне. Они переняли систему счисления шумеров. Египтяне тоже пользовались похожей системой счета.
Но все-таки подобный способ записи чисел не идеален и с развитием человечества развивалась и запись чисел.
Римские цифры.
Римские цифры появились 500 лет до н.э. Римская система счисления была очень распространена в Европе и считалась на то время, пока не придумали арабские цифры, идеальной.
С небольшими числами она вполне удобна, но для записи больших чисел очень сложна. Еще один недостаток: невозможно письменно делать вычисления. Их можно сделать только в уме, что, естественно, может породить большое количество ошибок.
Сейчас римские цифры тоже применяют, например, в записи века, порядкового номера монарха и т.п.
Арабские цифры.
В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
Запись цифры по числу углов
Далее произошло интересное: арабы переняли индийскую систему счисления и начали вовсю применять ее. В те времена мусульманский мир был очень развит, он имел очень тесные связи и с азиатской и европейской культурой и брал от них все самое совершенное и передовое на то время.
Математик Мухаммед Аль-Хорезми в IX веке составил руководство об индийской нумерации. Оно в XII веке попало в Европу и эта система счисления получило очень широкое распространение. Интересно, но именно из-за того, что к нам эти цифры пришли от арабов, мы их называем арабскими, а не индийскими.
Кстати, и само слово «цифра» — арабского происхождения. Арабы перевели индийское «сунья» и получилось «цифр».
Арабская система счисления называется позиционной. Это значит, что значение числа зависит от положения его в записи. То есть в числе 18 цифра 8 обозначает 8 единиц, а в числе 87 та же восьмерка обозначает 8 десятков. Позиционные системы наиболее совершенны. Но они произошли от непозиционных систем (которые, в принципе, существуют и сейчас) в результате развития человечества, его знаний и потребностей.
Интересно то, что современные арабские цифры сильно отличаются от тех, которые используем мы:
Современные арабские цифры
Вот такая история чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире.
Римская нумерация
Более двух тысяч лет назад появилась римская нумерация, т. е. в Древнем Риме числа записывали при помощи букв латинского алфавита.
I — 1; V — 5; X — 10; L — 50; C — 100; D — 500; M — 1000 — эти буквы называют римскими цифрами, а запись числа римскими цифрами называется записью числа в римской нумерации.
Для записи чисел римскими цифрами используются сложение и вычитание.
Договорились в случаях, когда в записи числа подразумевается сложение, меньшую цифру ставить после большей, а когда в записи числа подразумевается вычитание, меньшую цифру (вычитаемое) ставить перед большей (уменьшаемым).
Пример записи римских чисел
Так же как в записи чисел римскими цифрами подразумеваются сложение и вычитание, в записи чисел арабскими цифрами подразумеваются сложение и умножение:
Запись числа в таком виде называют суммой разрядных слагаемых.
Значит, значимость цифры зависит от её места в записи числа, т. е. от её позиции.
В таких случаях говорят, что число записано позиционным способом.
Что появилось раньше римская или арабская нумерация?
В привычной для нас системе записи чисел используются 10 цифр.
Счёт в ней идёт десятками, сотнями ( 10 десятков), тысячами ( 10 сотен) и т. д.
Поэтому наша система счёта называется десятичной, или десятичной системой счисления.
Используемые нами цифры называются арабской нумерацией. Она была изобретена в 400 году н.э в Индии. В 800 году н.э. арабская нумерация была заимстована арабами, а в 1200 году арабскую нумерацию начали применять в Европе. В России арабская нумерация стала использоваться при Петре I.
Римская нумерация возникла в древнем Риме между 900 и 800 годами до н.э. Таким образом, римская нумерация возникла раньше арабской.
Римская нумерация от 1 до 900000
Задачи на римскую нумерацию
Пример #1. Определи число, записанное римскими цифрами: MMDCCCXXII.
Решение:
Вспомним, что I — 1; V — 5; X — 10; L — 50; C — 100; D — 500; M — 1000.
Известно, что, записывая числа римскими цифрами, используют сложение и вычитание. Договорились в случаях, когда в записи числа подразумевается сложение, меньшую цифру ставить после большей, а когда в записи числа подразумевается вычитание, меньшую цифру (вычитаемое) ставить перед большей (уменьшаемым).
Поэтому MMDCCCXXII = 1000 + 1000 + 500 + 100 + 100 + 100 + 10 + 10 + 1 + 1 = 2822.
Ответ: MMDCCCXXII = 2822.
Пример #2. Определи число, записанное римскими цифрами: XXIX.
Решение:
XXIX = 10 + 10 + 9 = 29.
Ответ: XXIX = 29.
Пример #3. Укажи наименьшее пятизначное число.
Решение:
Известно: чтобы записать наименьшее пятизначное число, надо использовать в записи только цифру 1 — один раз — и цифру 0 — четыре раза.
Получим число 10000.
Ответ: наименьшее пятизначное число 10 000.
Пример #4. Укажи наименьшее одиннадцатизначное число.
Пример #5. Запиши словами число: 79 402 720 (запиши число строчными буквами, без всяких знаков препинания).
Пример #6. Сравни числа, если отдельные цифры в них заменены звёздочками: 27∗∗∗ и 28∗∗∗.
Решение:
Анализируя данные числа, в которых отдельные цифры заменены звёздочками:
27∗∗∗ и 28∗∗∗ — замечаем, что оба числа пятизначные, в старшем разряде десятков тысяч — одинаковые цифры, а в разряде единиц тысяч у первого числа цифра меньше, чем у второго, значит, первое число меньше второго, т. е. 27∗∗∗
Пример #7. Запиши число, которое на 90 меньше наибольшего четырёхзначного числа.
Решение
Наибольшее четырёхзначное число: 9999, а число которое на 90 меньше, чем наибольшее четырёхзначное: 9999 — 90 = 9909.
Ответ: 9909.
Пример #8. В фермерском хозяйстве 3 га заняты усадьбой и постройками, под посевами — 380 га, под сенокосом — 310 га, под лесом — 40 га и под выгоном — 110 га. Сколько всего земли в пользовании у фермера?
Решение
Для определения всей площади земли в пользовании у фермера нужно сложить площади, занятые усадьбой и постройками, посевами, сенокосом, лесом и выгоном. Получим:
3 + 380 + 310 + 40 + 110 = 843 га
Ответ: 843 га.
Пример #9. Запиши число 2458 в виде суммы разрядных слагаемых двумя способами.
Пример: 348 = 300 + 40 + 8 = 3 ⋅ 100 + 4 ⋅ 10 + 8.
Решение
Анализируя данный в задании образец записи числа в виде суммы разрядных слагаемых, применим его к данному четырёхзначному числу 2458.
Заметим, что старший разряд у него — единицы тысяч, поэтому запись получится следующей: 2458 = 2000 + 400 + 50 + 8 = 2 ⋅ 1000 + 4 ⋅ 100 + 5 ⋅ 10 + 8.
Ответ: 2458 = 2000 + 400 + 50 + 8 = 2 ⋅ 1000 + 4 ⋅ 100 + 5 ⋅ 10 + 8.
Пример #10. Запиши вместо ∗ число так, чтобы получилось верное равенство: 750000:∗=75000.
Решение:
Для того чтобы равенство 750000:∗=75000 было верным, вместо ∗ запишем число 10, т. к. в результате получено число, состоящее из тех же цифр, что и делимое, только сдвинутых на один разряд вправо, т. е. число уменьшилось в 10 раз.
Ответ: это число 10.
Пример #11. Определи все трёхзначные числа, для записи которых употребляются только цифры 1 и/или 5.
Решение:
Для определения всех трёхзначных чисел, в записи которых употребляются только цифры 1 и 5, начнём рассуждать так:
на первом месте (в разряде сотен) у этого числа может стоять цифра 1 или цифра 5, т. е. имеем
На втором месте (в разряде десятков) в каждом из этих двух случаев может быть также одна из цифр — 1 или 5.
На третьем месте (в разряде единиц) в каждом из полученных уже четырёх случаев может быть также одна из цифр — 1 или 5.
Продолжая подобные рассуждения и перебирая все возможные варианты получим
Таким образом, можно составить восемь чисел:
111;115;151;155;511;515;551;555.
Пример #12. Назови в каком разряде стоит цифра 7 в числе 7 890 214. Продолжи предложение: «Цифра стоит в разряде __________».
десятков
сотен
единиц миллионов
единиц тысяч
Решение:
Известно, что значимость цифры зависит от её места в записи числа, т. е. от её позиции.
Вспомним таблицу разрядов и название классов.
Таблица разрядов и классов
Таким образом, можно сделать вывод, что цифра 7 в числе 7 890 214 стоит в разряде единиц миллионов.
Ответ: цифра 7 стоит в числе 7 890 214 в разряде единиц миллионов.
Пример #14.Запишите пользуясь римской нумерацией свой возраст.
Пример #15. Запишите число, используя римскую нумерацию, 110 200.
Далее следует воспользоваться таблице приведенной выше и записать число 110 200 римскими цифрами.
110200 в римской нумерации
Пример #16.Нужно записать число 564 в римской нумерации.