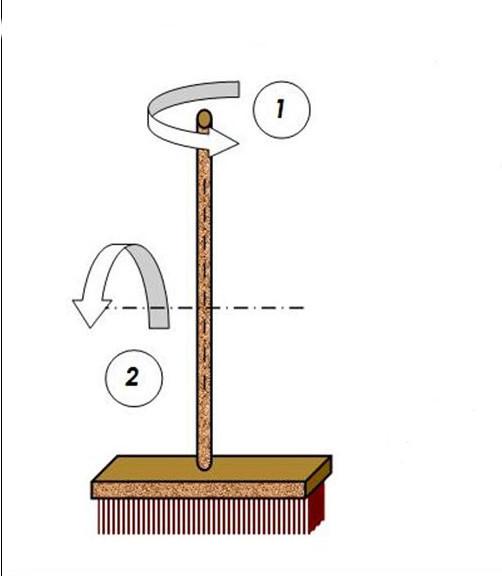
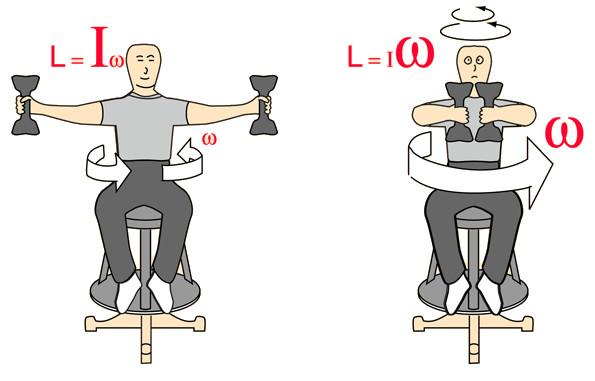
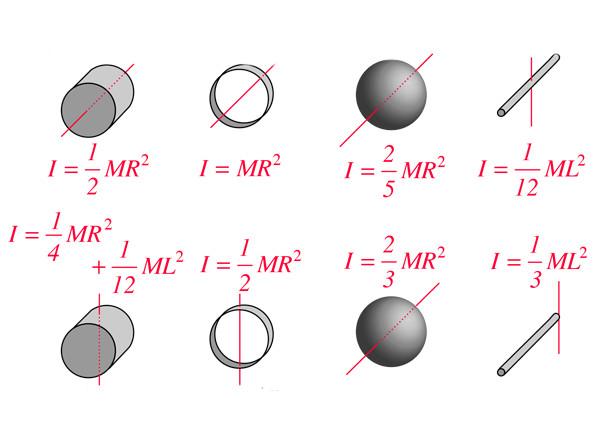Чем измеряется момент инерции
Момент инерции для чайников: определение, формулы, примеры решения задач
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
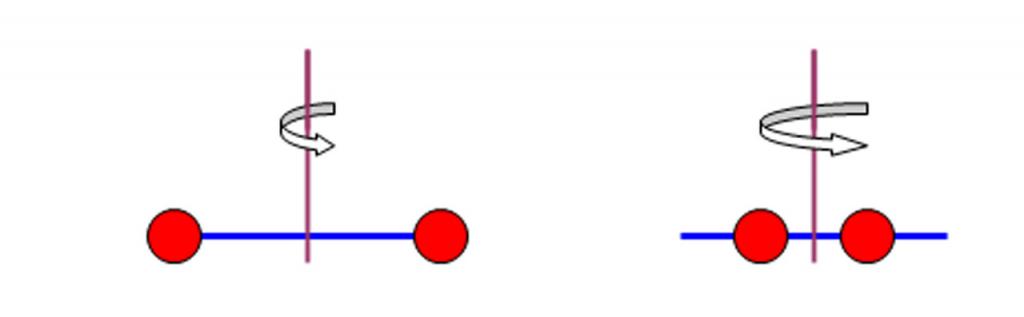
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
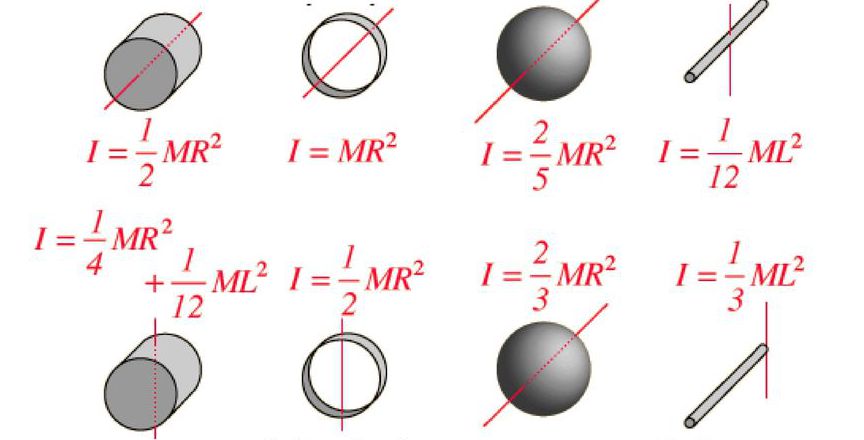
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Что такое момент инерции? В чем измеряется момент инерции? Пример задачи
Механика представляет собой один из основных разделов физики, в котором рассматриваются законы движения и равновесия тел. При количественном описании движения вращения важной величиной является момент инерции. В данной статье изучим эту величину. Кроме того, ответим на вопрос о том, в чем измеряется момент инерции твердого тела.
Понятие о моменте инерции для точки материальной
Как физическую величину, его определяют в виде произведения массы на квадрат радиуса вращения. Предположим, что существует некоторая материальная точка, которая имеет массу m. Она вращается вокруг оси, при этом радиус окружности равен r. При заданных условиях инерции, момент вычисляется в соответствии со следующей формулой:

Этой формулой можно пользоваться даже в случаях изучения тел со сложной формой. Главным условием справедливости равенства является наличие огромной разницы между расстоянием до оси вращения r и геометрическими размерами самого тела. Например, при расчете величины I для нашей планеты, которая вращается вокруг Солнца по круговой траектории, можно считать Землю материальной точкой, поскольку расстояние до звезды на несколько порядков превышает радиус планеты.
Величина I для тела произвольной формы
В случае, если геометрические размеры вращающегося тела незначительно отличаются от радиуса r, тогда следует принимать во внимание форму тела. С учетом названного фактора рассчитывают момент инерции с использованием следующей формулы:
По сути, это равенство является суммой моментов инерций всех материальных точек, которые образуют тело. При проведении практических вычислений, записанной формулой пользуются в несколько ином виде, который представлен ниже:
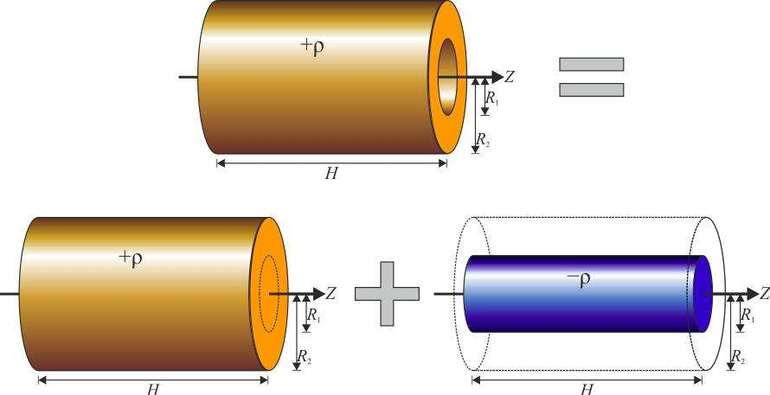
Как видно, интегрирование по массе m заменяется на интегрирование по объему V. Здесь греческой буквой ρ обозначена плотность. Если тело является однородным, то ρ будет постоянной величиной, которую можно вынести за знак интеграла. Если же масса неоднородно распределена по телу, то плотность будет функцией параметра r. Записанную формулу удобно использовать при определении I разных тел, потому что расчет выполняется с помощью мысленного деления тела на элементарные объемы dV.
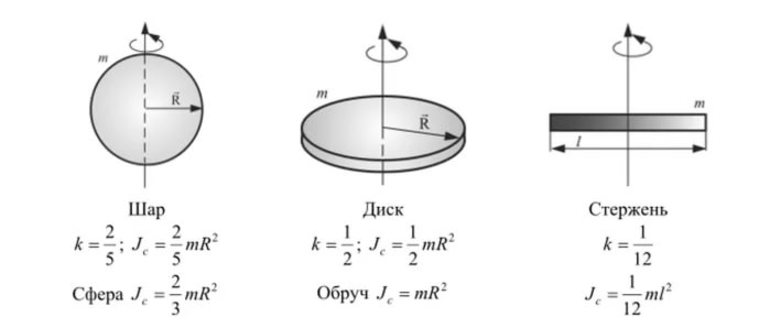
Результаты применения записанного выше равенства для геометрических тел идеальной формы, например, для сферы, цилиндра или стержня, собраны в соответствующие таблицы. В чем измеряется момент инерции? Ниже на рисунке приводятся величины I для некоторых тел. Как видим, все формулы линейно зависят от массы тел и от квадрата геометрического параметра.
В чем измеряется момент инерции тела?
Получив необходимые теоретические сведения для величины I, каждый легко сможет ответить на поставленный вопрос. Действительно, если взглянуть на формулу для I материальной точки, то, отвечая на вопрос о том, в чем измеряется момент осевой инерции, следует ответить, что в килограммах на квадратный метр. Сокращенно эта единица записывается кг*м2. Очевидно, что ту же самую единицу мы получим, если воспользуемся интегральным выражением через объем и плотность.
Отметим, что кг*м2 также можно записать, как м2*кг. Такая форма записи тоже допускается, однако, в практической физике ее не используют.
Поскольку и килограмм, и метр являются системными единицами измерения массы и длины, соответственно, то кг*м2 является также единицей СИ для момента инерции.
Не следует изучаемую единицу путать с другой, которая обозначается, как кг/м2. Хотя ее используют редко, и она не является единицей СИ, тем не менее она позволяет рассчитать соответствующее давление, если ее умножить на ускорение свободного падения.
Пример задачи
Разобравшись, в чем измеряется момент инерции, и как его вычислять, решим следующую задачу: необходимо определить момент инерции Земли, полагая ее материальной точкой.
Для успешного решения этой задачи следует знать всего два параметра: массу планеты и средний радиус ее солнечной орбиты. Оба значения можно посмотреть в соответствующих справочниках. Масса M и радиус орбиты R Земли равны:
Воспользовавшись выражением для вычисления инерции момента точки материальной, приходим к следующему результату:
I = M*R2 = 5,972*1024*(149,6*109)2 = 1,34*1047 кг*м2.
Мы получили гигантское значение. Если сравнить его с моментом инерции Земли относительно ее собственной оси, то окажется, что он будет в миллиард раз меньше рассчитанной величины. Таким образом, приближение материальной точки вполне уместно для рассмотренной задачи.
Единицы измерения момента инерции
Моментом инерции тела, совершающего вращательные движения вокруг некоторой оси называют физическую величину ($J$), равную:
Проще всего единицу измерения момента инерции тела определить, если рассмотреть материальную точку, вращающуюся вокруг неподвижной оси:
Из выражения (3) очевидно, что:
Грамм-сантиметр в квадрате соотносится с единицей измерения момента инерции системы СИ как:
Момент инерции, не имеющий единицы измерения
Примеры задач с решением
Задание. Каким будет единица измерения момента инерции материальной точки, которая вращается около неподвижной оси, если получить ее из основного закона динамики вращательного движения?
Решение. Формулу закона динамики вращательного движения для материальной точки представим как:
Единицей измерения момента сил в системе СИ является:
Угловое ускорение материальной точки найдем как:
В соответствии с выражением (1.3) имеем:
Ответ. Исходя из основного закона динамики вращательного движения, получаем, что в системе СИ момент инерции измеряется в килограммах, умноженных на метр в квадрате.
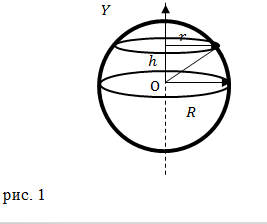
Из рис.1 очевидно, что:
Элементарный момент инерции (диска) запишем как:
где масса выделенного диска ($dm=\rho dV$) равна:
\[dm=\rho \pi r^2dh\ \left(2.3\right).\]
Получим момент инерции шара, относительно оси, которая проходит через его центр масс, интегрируя выражение (2.4) по объему шара:
Плотность однородного шара равна:
то выражение (2.5) преобразуем к виду:
Окончательно формулу для нахождения момента инерции Земного шара запишем как:
Вычислим момент инерции Земли:
\[1\ т=1000\ кг,\ следовательно,\ 1\ т\cdot м^2=1000\ кг\cdot м^2.\]
В чем измеряется момент инерции, какой его физический смысл?
Вращение механической системы является одним из распространенных способов движения тел в пространстве. Этот тип движения характеризуется набором физических величин, в названии которых присутствует слово «момент». Данная статья посвящена ответу на следующий вопрос: в чем измеряется момент инерции.
Характеристика движения вращения
Каждый хорошо представляет, о чем идет речь. Достаточно упомянуть вращение колес автомобиля, велосипеда или чертового колеса в парке аттракционов. Если говорить о больших пространствах и массах, то можно вспомнить о вращении нашей Земли вокруг звезды Солнце.
В физике все отмеченные в примерах выше перемещения объектов принято описывать следующим уравнением:
Если внешние силы не оказывают никакого момента M¯, тогда уравнение выше переходит в так называемый закон сохранения углового момента L¯, то есть:
В физику угловой момент (его также называют моментом импульса) вводится как векторное произведение линейного импульса точки с массой m и скоростью v¯ на вектор r¯, который перпендикулярен оси вращения и соединяет ее с этой точкой, то есть:
Если воспользоваться понятием об угловой скорости ω¯ и ее связью с аналогичной линейной величиной v¯, то это равенство можно переписать в таком виде:
Величина I в физике
В последнем выражении предыдущего пункта величина I равна произведению массы точки на квадрат ее расстояния до оси, то есть:
Поскольку все реальные тела не являются материальными точками, а имеют определенные пространственные параметры и форму, то для определения их момента инерции используется исходное выражение выше, которое становится подынтегральным. Общая формула для I тела выглядит так:
Эта математическая формула говорит о том, что чтобы посчитать момент инерции всего тела его нужно мысленно разбить на материальные точки dm, умножить их на квадрат дистанции до оси вращения, а затем все результаты сложить.
В чем измеряется момент инерции тела?
Поскольку выше была приведена основная информация, которую необходимо знать для понимания рассматриваемой величины, то каждый может ответить на вопрос этого пункта. Тем не менее рассмотрим его более подробно.
Итак, в каких единицах измеряется момент инерции тела? И формула для материальной точки, и общее выражение для тела произвольной формы приводят к одному и тому же ответу: величина I абсолютно любой вращающейся системы измеряется в килограммах на квадратный метр (кг*м 2 ).
Конечно же, для выражения момента инерции можно использовать любые долевые единицы от указанного стандарта в СИ. Например, для систем с небольшими массами и линейными размерами I может выражаться в граммах на сантиметр в квадрате (г*см 2 ). Наоборот, в космических масштабах могут применяться мегатонны на астрономические единицы в квадрате (чаще всего используется все же кг*м 2 с числом 10, возведенным в большие степени).
Отвечая на вопрос, в чем измеряется момент инерции, следует упомянуть иной подход для выражения этой величины. Для его понимания запишем формулу для изменения момента импульса:
M¯ = dL¯ / dt = I * dω¯ / dt, следовательно, I = M¯ * dt / dω¯.
Смысл величины I
Рассмотрев вопрос, в каких единицах измеряется момент инерции, можно сказать и о том, что означает эта величина.
Момент инерции сечения
Основные понятия и суть
Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.
Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах. В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате. Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r 2 j. В ней:
То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.
М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.
Вычисление параметра
Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.
Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.
Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2. Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.
Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.
Методика решения
Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:
Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования. Понимая физический смысл момента инерции, можно отметить следующие зависимости:
Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.
Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.
Моменты простейших объектов
Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:
При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.
Теорема Гюйгенса — Штейнера
Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:
Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.
Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).
В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.
Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.
Пример задачи
Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.
Момент вращения относительно диска определяется с помощью выражения I1 = m* d 2 / 2. Для решения задачи она будет выглядеть Io = m* d 2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.