Чем меньше давление тем больше скорость

Чем меньше давление тем больше скорость

В этом параграфе мы применим закон сохранения энергии к движению жидкости или газа по трубам. Движение жидкости по трубам часто встречается в технике и быту. По трубам водопровода подается вода в городе в дома, к местам ее потребления. В машинах по трубам поступает масло для смазки, топливо в двигатели и т. д. Движение жидкости по трубам нередко встречается и в природе. Достаточно сказать, что кровообращение животных и человека — это течение крови по трубкам — кровеносным сосудам. В какой-то мере течение воды в реках тоже является разновидностью течения жидкости по трубам. Русло реки — это своеобразная труба для текущей воды.

Как известно, неподвижная жидкость в сосуде согласно закону Паскаля передает внешнее давление по всем направлениям и во все точки объема без изменения. Однако, когда жидкость течет без трения по трубе, площадь поперечного сечения которой на разных участках различна, давление оказывается неодинаковым вдоль трубы. Выясним, почему давление в движущейся жидкости зависит от площади поперечного сечения трубы. Но сначала ознакомимся с одной важной особенностью всякого потока жидкости.

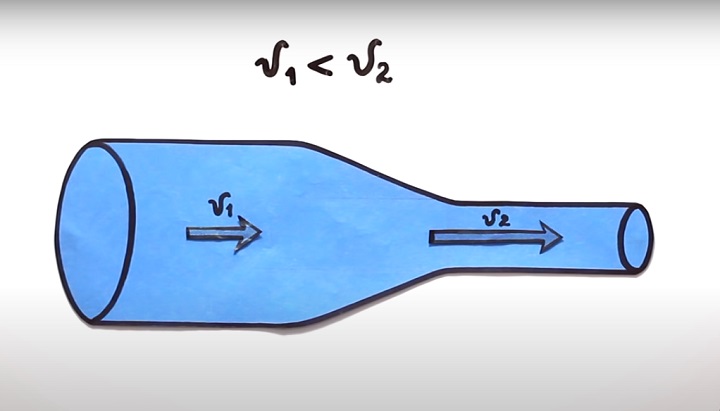
Предположим, что жидкость течет по горизонтально расположенной трубе, сечение которой в разных местах различное, например по трубе, часть которой показана на рисунке 207.

Если бы мы мысленно провели несколько сечений вдоль трубы, площади которых соответственно равны и измерили бы количество жидкости, протекающей через каждое из них за какой-то промежуток времени то мы обнаружили бы, что через каждое сечение протекло одно и то же количество жидкости. Это значит, что вся та жидкость, которая за время проходит через первое сечение, за такое же время проходит и через третье сечение, хотя оно по площади значительно меньше, чем первое. Если бы это было не так и через сечение площадью за время проходило, например, меньше жидкости, чем через сечение площадью то избыток жидкости должен был бы где-то накапливаться. Но жидкость заполняет всю трубу, и накапливаться ей негде.

Как же может жидкость, протекшая через широкое сечение, успеть за такое же время «протиснуться» через узкое? Очевидно, что для этого при прохождении узких частей трубы скорость движения должна быть больше, и как раз во столько раз, во сколько раз площадь сечения меньше.

Действительно, рассмотрим некоторое сечение движущегося столба жидкости, совпадающее в начальный момент времени с одним из сечений трубы (рис. 208). За время эта площадка переместится на расстояние которое равно где — скорость течения жидкости. Объем V жидкости, протекшей через сечение трубы, равен произведению площади этого сечения на длину

В единицу же времени протекает объем жидкости —

Объем жидкости, протекающей в единицу времени через сечение трубы, равен произведению площади поперечного сечения трубы на скорость течения.

Как мы только что видели, этот объем должен быть одним и тем же в разных сечениях трубы. Поэтому, чем меньше сечение трубы, тем больше скорость движения.

Сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое

же время через любое другое сечение.

При этом мы считаем, что данная масса жидкости всегда имеет один и тот же объем, что она не может сжаться и уменьшить свой объем (о жидкости говорят, что она несжимаема). Хорошо известно, например, что в узких местах реки скорость течения воды больше, чем в широких. Если обозначить скорость течения жидкости в сечениях площадями через то можно написать:

Отсюда видно, что при переходе жидкости с участка трубы с большей площадью сечения на участок с меньшей площадью сечения скорость течения увеличивается, т. е. жидкость движется с ускорением. А это по второму закону Ньютона означает, что на жидкость действует сила. Что это за сила?

Этой силой может быть только разность между силами давления в широком и узком участках трубы. Таким образом, в широком участке давление жидкости должно быть больше, чем в узком участке трубы.

Это же следует из закона сохранения энергии. Действительно, если в узких местах трубы увеличивается скорость движения жидкости, то увеличивается и ее кинетическая энергия. А так как мы приняли, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. О какой же потенциальной энергии здесь идет речь? Если труба горизонтальна, то потенциальная энергия взаимодействия с Землей во всех частях трубы одна и та же и не может измениться. Значит, остается только потенциальная энергия упругого взаимодействия. Сила давления, которая заставляет жидкость течь по трубе, — это и есть упругая сила сжатия жидкости. Когда мы говорим, что жидкость несжимаема, то имеем лишь в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление упругих сил, неизбежно происходит. Эти силы и создают давление жидкости. Вот это сжатие жидкости и уменьшается в узких частях трубы, компенсируя рост скорости. В узких местах труб давление жидкости должно быть поэтому меньше, чем в широких.

В этом состоит закон, открытый петербургским академиком Даниилом Бернулли:

Давление текущей жидкости больше в тех сечениях потока, в которых скорость ее движения меньше, и,

наоборот, в тех сечениях, в которых скорость больше, давление меньше.

Как это ни покажется странным, но когда жидкость «протискивается» через узкие участки трубы, то ее сжатие не увеличивается, а уменьшается. И опыт хорошо это подтверждает.

Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками — манометрами (рис. 209), то можно будет наблюдать распределение давления вдоль трубы. В узких местах трубы высота столба жидкости в манометрической трубке меньше, чем в широких. Это означает, что в этих местах давление меньше. Чем меньше сечение трубы, тем больше в ней скорость течения и меньше давление. Можно, очевидно, подобрать такое сечение, в котором давление равно внешнему атмосферному давлению (высота уровня жидкости в манометре будет тогда равна нулю). А если взять еще меньшее сечение, то давление жидкости в нем будет меньше атмосферного.

Такой поток жидкости можно использовать для откачки воздуха. На этом принципе действует так называемый водоструйный насос. На рисунке 210 изображена схема такого насоса. Струю воды пропускают через трубку А с узким отверстием на конце. Давление воды у отверстия трубы меньше атмосферного. Поэтому

газ из откачиваемого объема через трубку В втягивается к концу трубки А и удаляется вместе с водой.

Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях, и может стать меньше атмосферного. В некоторых случаях для этого даже не требуется трубы.

Можно проделать простой опыт. Если дуть на лист бумаги вдоль его поверхности, как показано на рисунке 211, можно увидеть, что бумага станет подниматься вверх. Это происходит из-за понижения давления в струе воздуха над бумагой.

Такое же явление имеет место при полете самолета. Встречный поток воздуха набегает на выпуклую верхнюю поверхность крыла летящего самолета, и за счет этого происходит понижение давления. Давление над крылом оказывается меньше, чем давление под крылом. Именно поэтому возникает подъемная сила крыла.

1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем нефти проходит через трубу диаметром 1 м в течение 1 ч?

2. Измерьте количество воды, вытекающей из водопроводного крана за определенное время Определите скорость течения воды, измерив диаметр трубы перед краном.

3. Каким должен быть диаметр трубопровода, по которому должно протекать воды в час? Допустимая скорость течения воды 2,5 м/сек.

Источник

Формулировка закона Бернулли и его математическое выражение

Обновлено: 02 Июня 2021

Принцип Бернулли заложил основы знания о движении жидкости, которое впоследствии перешло в самостоятельную науку — гидродинамику.

Физическая сущность закона Бернулли

Швейцарский математик и физик Даниил Бернулли родился в 1716 году в Голландии. За свою научную карьеру он получил звания Почетного члена Берлинской, Петербургской и Парижской академии наук, являлся членом Лондонского королевского общества. Главным научным трудом ученого является работа «Гидродинамика, или изъяснение сил и движений жидкости», опубликованная в 1733 году. Именно в этой книге были описаны физические основы механики жидкости.

Закон, названный его именем, Бернулли сформулировал во время работы в России, изучая взаимосвязь давления жидкости с ее скоростью. В математическом выражении он определяется уравнением Бернулли. Давайте разберемся, в чем состоит сущность закона.

Для начала определим, что закон Бернулли рассматривает движение потока несжимаемой идеальной жидкости, на которую действуют только силы тяжести и силы упругости.

Идеальная жидкость — это жидкость, в которой полностью отсутствует внутреннее трение и теплопроводность, ввиду чего, она лишена касательных напряжений между соседними слоями.

Подобная идеализация применяется при рассмотрении течения в гидродинамике. В законе Бернулли рассматривается стационарное течение жидкости — это движение слоев жидкости относительно друг друга и относительно ее самой, при котором скорость потока в некой конкретной точке не меняется, сохраняя свое постоянное значение. Давление при стационарном течении идеальной жидкости одинаково во всех поперечных сечениях трубки тока.

Для наглядности рассмотрим стационарное течение идеальной жидкости по трубе переменного сечения. В одном месте сечение этой трубки равно S1, а в другом — S2. При стационарном потоке через все сечения за определенный промежуток времени пройдет одинаковый объем жидкости, так как в ином случае, невозможность сжатия привела бы к ее разрыву. Таким образом, мы получаем уравнение неразрывности струи, определяющее соотношение между скоростью течения (v) и площадью сечения (S): S1v1=S2v2

При этом скорость давление в сечении S1 меньше, чем в сечении S2. Как вы думаете, в каком из сечений скорость течения жидкости будет больше? Казалось бы, что по логике, скорость должна увеличиваться в том месте, где больше давление. Однако, согласно закону Бернулли, скорость увеличивается с уменьшением площади сечения. В этом-то и состоит парадоксальность принципа.

Закон Бернулли гласит, в тех участках течения жидкости или газа, где скорость больше, давление меньше, и наоборот, с увеличением давления жидкости, протекающей в трубе, скорость ее движения уменьшается. То есть, где больше скорость (v), там меньше давление (p).

Чтобы убедиться в этом, достаточно провести небольшой опыт из подручных средств. Возьмите два шара одного размера и подвесьте их так, чтобы между ними сохранялось небольшое расстояние. Подуйте между шарами или пустите воздух из фена. Шары вместо того, чтобы отдалиться, притянутся друг к другу. Это прямое следствие описанного закона, так как в том месте, куда вы дули, давление стало уменьшаться, а скорость шаров возросла, приблизив их друг к другу.

Закон Бернулли как следствие закона сохранения энергии

Из уравнения неразрывности следует, что в идеальной жидкости сумма статистического и динамического давлений и скоростного напора постоянна в любом сечении вдоль трубы. Являясь следствием закона сохранения, вывод уравнение Бернулли для элементарной струйки жидкости выглядит так:

\rho\) — плотность жидкости, \(

v\) — скорость потока, \(

h\) — высота, на которой находится рассматриваемый элемент жидкости, \(

p\) — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, \(

g\) — ускорение свободного падения.

При этом давление P — это статическое давление, которое получается в результате взаимодействия соседних слоев жидкости. Величина ρv2/2 — это динамическое давление, обусловленное движением жидкости, а ρgh — это давление, образованное массой вертикального столба жидкости высотой h, создаваемое силой тяжести.

Все эти величины имеют специальные обозначения, где h — высота положения или геометрический напор, P / ρ∙g — пьезометрический напор, v2 / 2g — скоростной напор.

Сумма трех слагаемых уравнения называется полным напором (H), то есть для идеальной жидкости при стационарном течении сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.

Для трубы, расположенной горизонтально, где величина высоты остается неизменной, уравнение Бернулли упрощается и выглядит так:

Проявление закона Бернулли в жизни

Закон Бернулли описывает одно из основных свойств гидравлики. Эффект, описанный швейцарским ученым, широко проявляется в природе и быту. Также широко его применение в технике. На основе принципа Бернулли работают такие приборы, как пульверизатор, водоструйный насос, аэрограф.

Чтобы понять механизм устройства, рассмотрим строение пульверизатора, которое включает в себя вертикальную трубку и горизонтальное сопло. Вертикальную трубку опускают в жидкость, в то время как по соплу пропускают воздух. Атмосферное давление, которое больше давления в струе воздуха, заставляет жидкость подниматься по трубке. Следовательно, при попадании в струю воздуха, происходит распределение жидкости.

В повседневной жизни закон Бернулли можно наблюдать, сидя у камина. При сильном ветре скорость воздушного потока возрастает, и, соответственно, падает давление. И так как давление воздуха в комнате выше, пламя, уходит вверх по дымоходу.

Это свойство используется и в аэродинамике для объяснения того, как возникает подъемная сила самолета или другого летательного аппарата, которое тяжелее воздуха.

В истории имеются и случаи отрицательного проявления закона. В 1912 году произошло столкновение океанского парохода «Олимпик» с гораздо меньшим по масштабам крейсером «Гаук», который плыл параллельно пароходу на расстоянии около 100 метров. Вдруг «Гаук» резко двинулся прямо на «Олимпик» и протаранил его силой удара. Так как два корабля были друг к другу слишком близко, скорость воды между ними стала больше, чем с другой стороны, вызвав дополнительную силу. Следовательно, вместо того, чтобы отдалиться, корабли притянулись друг к другу, что и стало причиной катастрофы.

В природе закон Бернулли проявляется во время урагана, когда из-за сильного ветра с домов слетают крыши. Это происходит, потому что скорость, с которой движется воздух вверху, очень большая, тогда как на чердаке она равна нулю. Как вы уже узнаете, там, где скорость потока больше, давление меньше, а там, где скорость меньше, давление больше. В результате образовавшейся разности давлений ураган и срывает кровлю.

Существует еще большое количество интересных примеров, изучение которых во многом упрощает усвоение закона Бернулли. Если вам нужно определить проявление закона в каком-то конкретном явление, обращайтесь к специалистам сервиса Феникс.Хелп, которые помогут решить задачу любой сложности.

Источник

Закон Бернулли для чайников и учёных

Предисловием можно считать «За что физики не любят математиков»: http://proza.ru/2015/11/16/160

«Наука должна быть весёлая, увлекательная и простая. Таковыми же должны быть и учёные» (П.Л. Капица). и преподаватели. Но более всего наука должна быть честная. И «Ни один человек не должен покидать стены наших университетов без понимания того, как мало он знает» (Роберт Оппенгеймер). и как мало знают учёные. А чтобы так оно и было, нужно срезать профессора математической лженауки на первой же лекции. И прежним занудой он уже не будет. Знаю, что говорю, и привожу очередной пример.

Правильный ответ: неподвижные поверхностные манометры на картинке вверху показывают давление потоков, так как для измерения давления в потоках нужны такие манометры или датчики давления, которые находились бы внутри потоков и двигались вместе с ними. Давление внутри потоков, знаете ли, почти всегда статично. Но таких мобильных манометров, которые могли бы быть неподвижными относительно ламинарных потоков, нет в опытах к теме «Закон Бернулли». Однако вывод сделан такой, словно они есть, словно давление внутри потоков уже измерено. «Для физика должно существовать только то, что измерено» (Нильс Бор). а не то, что можно подумать, придумать, недодумать и сосчитать. Сосчитать то, чего нет, может каждый.

А тем-то он и хуже, что никакой научности и сложности для понимания в нём нет. К тому же, давление потока на поперечную поверхность или «скоростной напор» измеряется с помощью Г-образной «трубки Пито», вставляемой в поток загнутым концом навстречу потоку. Отсюда: давление в самом потоке примерно равно среднему арифметическому от показаний «трубки Пито» и «трубки у Бернулли». Более того, в ньютоновской механике уменьшение силы давления на параллельную потоку или телу поверхность с увеличением скорости потока или тела и одновременное увеличение давления потока или тела на поперечную поверхность можно объяснить простым векторным разложением силы давления потока или тела. Чем больше скорость автомобиля, тем меньше его вес и давление на дорожное полотно; чем больше скорость потока, тем меньше его давление на стенки трубы. Пусть пока будет так.

Конечно, наши выводы профессору будут сильно не по нутру. Но если он будет ещё в состоянии что-то говорить и продолжит настаивать на том, что «С увеличением скорости потока давление внутри потока уменьшается», то срежем его вторым вопросом: «Почему причина и следствие в формулировке общепризнанного закона Бернулли переставлены местами?».

Можно короче: «Чем больше падение давления в потоке или на данном участке трубы, тем больше здесь и скорость самого потока». И это будет тривиальный закон потоков, у которого уже есть все пять обязательных признаков новой истины: простота, ясность, универсальность, «предсказательная сила» и антинаучность. Опровергнуть этот закон сможет только тот, кто создаст поток жидкости или газа, движущийся из области пониженного давления в область повышенного давления, то есть против действия превосходящих сил давления и упругости. Шутка.

Инженер-аэродинамист сформулирует свой закон потоков примерно так: «Давление потока на параллельную или отрицательно наклонную поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока или поверхности (верхней поверхности крыла); а давление потока на поперечную или положительно наклонную поверхность всегда тем больше давления в самом потоке, чем больше скорость потока или поверхности (нижней поверхности атакующего крыла)». И это будет качественный закон взаимодействия потоков с поверхностями, так как в каждом конкретном случае величина давления потока на поверхность зависит не только от скорости потока, но и от физических свойств потока и поверхности, поэтому она не вычисляется, а только измеряется. Следовательно, математикам и в аэродинамике делать особо нечего.

Действие этих двух законов во многих опытах и явлениях складывается или накладывается, поэтому наблюдаемый результат нельзя объяснять действием только какого-то одного закона. Но объединённого закона Бернулли или третьего математического закона потоков никогда не было, поэтому как определить «личную долю» каждого закона в результате того или иного опыта к теме «Закон Бернулли» не знает ни один математик. но знает каждый инженер. Он просто измеряет с помощью манометров и динамометров давление в потоке и давление потока при различной скорости потока, а потом лишь сравнивает результаты измерений. и никаких теорий потоков для него словно не существует. Действительно, зачем вычислять, если можно измерить.

Качественный закон потоков гласит: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». Можно короче: «Давление потока на параллельную поверхность всегда тем меньше, чем больше хаос в движении частиц потока».

В гидродинамике давление всегда первично, а скорость потока вторична; в аэродинамике скорость крыла всегда первична, а давление неподвижной атмосферы на него всегда вторично. Плоское крыло самолёта или птицы не изменяет давление в неподвижной атмосфере, а изменяется с увеличением скорости и угла атаки лишь взаимодействие быстрого крыла с атмосферой. Но в наших рассуждениях крыло чаще всего неподвижно, а это атмосфера «набегает» на крыло, словно всё происходит в аэродинамической трубе или в статическом (стационарном) потоке. Просто так нам удобнее рассуждать и объяснять.

У инженеров всё, что летает, делает это по причине совсем небольшой положительной разницы или асимметрии атмосферного давления на крыло. Появление подъёмной силы как раз и обусловлено качественным законом потоков: «Давление атмосферного потока на верхнюю отрицательно наклонную поверхность быстрого крыла тем меньше давления в самой атмосфере, чем больше хаос и разрежение частиц воздуха над ней; а давление потока на нижнюю положительно наклонную поверхность крыла тем больше атмосферного давления, чем больше скорость крыла, его угол наклона или атаки и деформация или уплотнение упругого воздуха под быстрым крылом». Как диагональ делит прямоугольник на два равных треугольника, так и плоское атакующее крыло делит набегающий поток на две самостоятельные и равнозначные причины возникновения подъёмной силы.

Вспомним, атмосферное давление на уровне моря равно 1,0033 кг/см2. Это очень большая сила, которая давит на неподвижное плоское крыло совершенно одинаково и сверху, и снизу. Если атмосферное давление со стороны одной из поверхностей крыла убрать, то со стороны противоположной поверхности тут же возникнет сила равная 10033 кг/м2. Да, 10 тонн на каждый квадратный метр крыла! И что мы имеем: орёл весом 4 кг, имея площадь «несущих поверхностей» как раз 1м2, почти неподвижно парит в вышине при положительной разнице атмосферных давлений на его крылья всего 0,04% от теоретически возможного 1 кг/см2; АН-2 («кукурузник») летает горизонтально на разности 0,4% атмосферного давления; а скоростному современному пассажирскому авиалайнеру для горизонтального полёта достаточно и 5% от 1 кг/см2 или 50 г/см2.

Идеальный или самый эффективный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло. И это для передовых инженеров уже аксиома или «новая аэродинамика», а Природа это знала ещё со времён первых летающих насекомых и птеродактилей. Так вот, асимметричное атмосферное давление на совершенно плоское крыло возникает и при его нулевом угле наклона к вектору движения набегающего атмосферного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая. В воде «эффект хаоса над крылом» проявляется ещё значительно сильнее.

Это утверждение доказано самой эволюцией живой природы и передовой практикой авиастроения. Смотрим на расправленное крыло любой птицы: сверху оно бархатистое и может играть всеми цветами радуги, что физику говорит о дисперсии света на мельчайших неровностях на поверхности, а снизу – всегда очень плотное, гладкое и со стальным отливом. Смотрим на современный пассажирский «Боинг»: сверху он словно матовый, а снизу – зеркально гладкий. И пусть та положительная разница в атмосферном давлении на крыло, которая возникает только по причине различного качества покрытия его аэродинамических поверхностей, будет и недостаточной для полёта, но именно она и позволит самолёту или птице лететь горизонтально с меньшим углом атаки, то есть с меньшим лобовым сопротивлением, экономя топливо и силы.

Инженеры «Боинга» говорят, что уже экономят на «эффекте хаоса над крылом» до 7-ми процентов топлива, а это огромные деньги. Смотрите фотографии «Боингов» и читайте по запросу «Аэродинамика Боинг». А наши дурни из Сколково одной краской покрывают весь Боинг. Смотрите по запросу «Красим Боинг». Кожа акулы тоже только кажется гладкой, а на ощупь она сравнима с наждачной бумагой. Шершавая кожа способствует образованию хаоса в пограничном слое воды, что ещё больше уменьшает её давление на быструю акулу. И таких примеров «мильён».

Однако вторым законом потоков объясняются не только опыты к теме «Закон Бернулли», но ещё один раз доказывается нечто совсем другое, позволяющее увидеть истоки математического идеализма в физике и похоронить математическую физику, как науку о природе. «Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру» (А. Эйнштейн). Сейчас мы эту словесную формулу математического идеализма просто-напросто докажем. Вернее, я докажу, а вы. согласитесь.

«Все жидкости и газы на Земле имеют вес и находятся под давлением веса собственных и выше расположенных слоёв» (Архимед). Поэтому все прозрачные жидкости и газы состоят из примерно одинаковых, равноудалённых и условно неподвижных (колеблющихся или дрожащих) частиц, находящихся в состоянии взаимного отталкивания и относительного (или чуткого) равновесия и взаимно отталкивающихся в газах на расстояниях много больших, чем в жидкостях. Отсюда: давление в любой точке водоёма или атмосферы равно напряжению взаимного отталкивания равноудалённых частиц в этой точке, и по силе оно равно весу всех частиц над этой точкой. Уберите атмосферное давление, и капля воды тут же исчезнет, разлетевшись на молекулы, а аквариум с водой словно взорвётся. И повинно в том будет как раз-таки «напряжение взаимного отталкивания равноудалённых частиц». Смотрите по запросу «Современный Архимед. Трактат «О плавающих телах» и «К физике антигравитонов». Там есть опыты, позволяющие буквально увидеть неподвижность колеблющихся частиц в жидкостях и в газах. Особенно показателен опыт по мгновенному замерзании переохлаждённой воды при её встряхивании в пластиковой бутылке. Многие его знают, но не понимают.

Способность атомов и молекул к движению взаимного отталкивания пропорциональна температуре. А температура – это «опосредованное мерило» интенсивности атомных и внутриатомных движений и величины гравитационных моментов (квантов, импульсов) атомов, передающихся от атома к атому путём индукции.

И ещё. Всем теоретикам и преподавателям на засыпку: «Какой теорией руководствовались братья Райт, когда делали свой воздушный винт, который у них получился с КПД 78-80%, если научной аэродинамики ещё не было, а КПД самых современных пропеллеров из дерева не превышает 85%?».

Хотелось бы услышать возражения или замечания, но их почему-то нет. Видимо, с тем, что мы живём в эпоху математических лженаук, уже никто не спорит.

Воображеньем прозорливым
К догадкам верным нас несло…
Но сонм учёных кропотливых
Свернул наш поиск — на число.

И лязгом счёта оглушённый
Забыл наш ум — решенья ключ…
Стал слепнуть, в шоры цифр втеснённый.
А был так зряч и так могуч!

Уж цифре памятник построен,
Распята Истина на нём.
Поклонник счёта, жрец и воин
Простёрся ниц перед числом:

Не осознать бедняге в заблужденье,
Как много лжи за ширмой исчисленья!

Источник