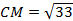Чем меньше косинус тем больше угол

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

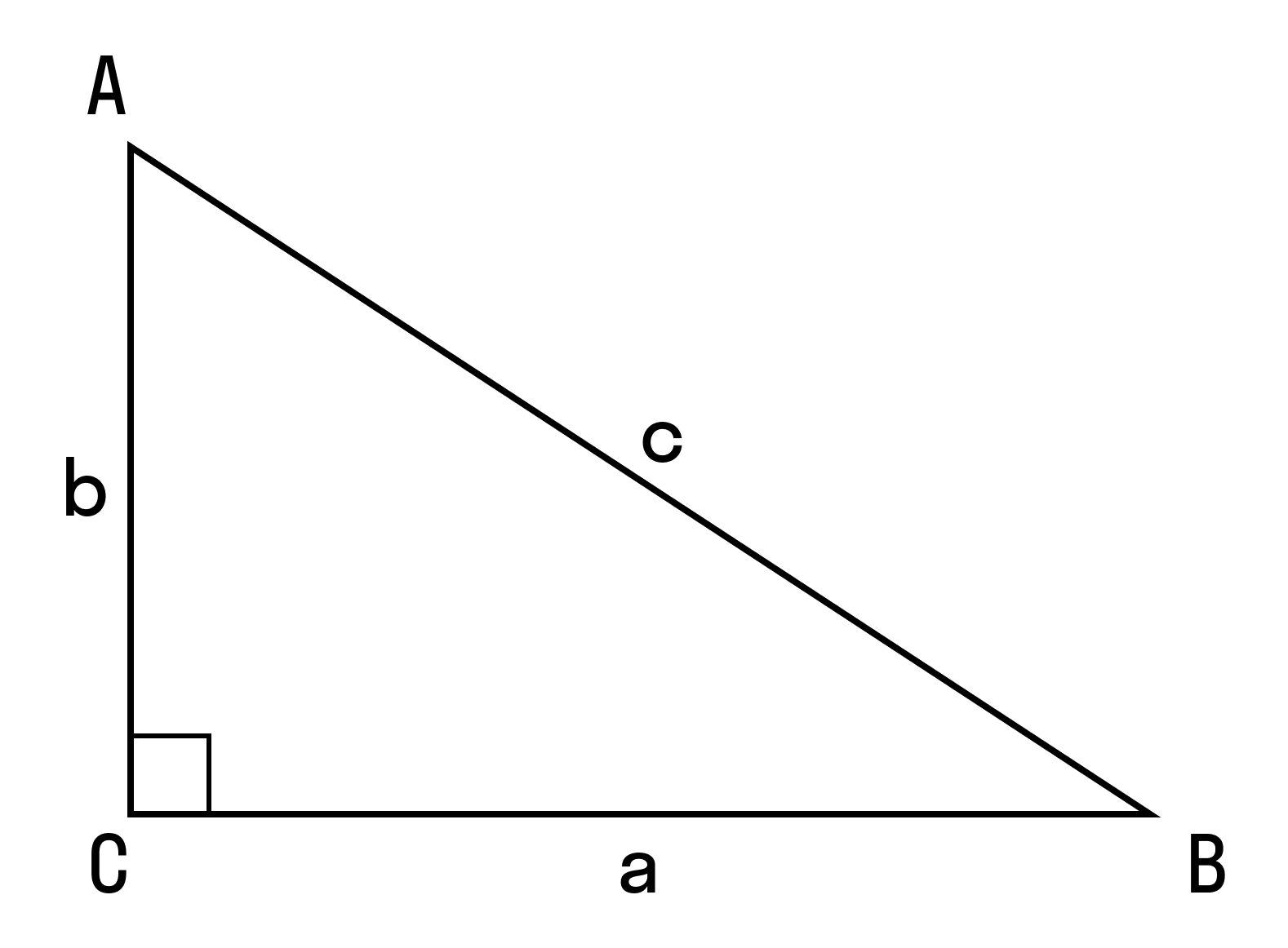
Синус, косинус, тангенс острого угла

Тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника.

Основное тригонометрическое тождество

Если мы возьмем гипотенузу, равную 1, то это определение можно упростить до:

Тогда теорему Пифагора можно переформулировать так:

$$(\sin \alpha)^2 + (\cos \alpha)^2 = 1$$

Или другая форма записи без скобок:

$$\sin^2 \alpha + \cos^2 \alpha = 1$$

Формулы приведения для острого угла

Возрастание и убывание

Чем больше один из острых углов прямоугольного треугольника, тем меньше другой. Отсюда следует, с учетом ОТТ, для этих углов:

Мнемоническое правило

Правило для косинуса

Синусу не остается ничего другого, кроме «противолежать».

«Длинный» косинус в паре с «коротким» прилежащим катетом, «короткий» синус в паре с «длинным» противолежащим катетом.

Правило для ОТТ

В семье Синичкиных (Sin) праздник. К ним в отпуск приезжает дочка с мужем, семья Косичкиных (Cos). Вот двое Синичкиных радостно бегут навстречу Косичкиным. Они обнимаются (+). И образуют одну большую семью: 1.

Синус в строительстве

Возьмите 10-метровый столб и поднимите его с земли на 45 градусов. Верхушка столба будет находиться на высоте

А 8-метровый столб будет на высоте

Подобные манипуляции со столбами очень полезны в строительстве (пирамиды сами себя не рассчитают). К сожалению, спустя тысячи лет у нас твердо закрепилась мысль, что смысл синуса в возможности вычислить высоту треугольника по гипотенузе и углу. Для краткости мыслительного процесса думаем «синус=высота». Это нормально, главное не застревать на этом, а смотреть шире.

Расчеты в Excel

Пусть известно расстояние до дерева. Нужно узнать его высоту:

Источник

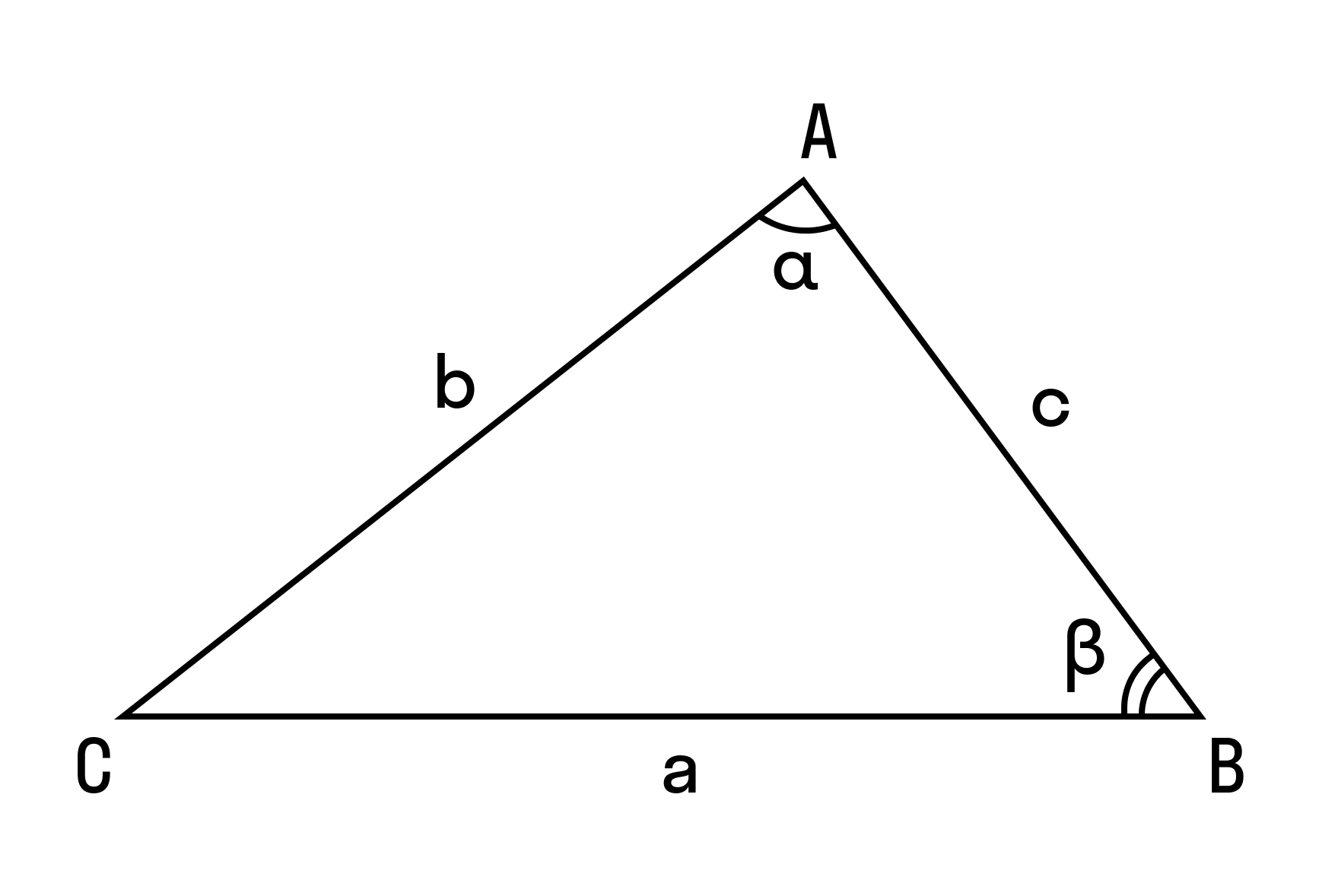
Теорема косинусов и синусов

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

Приравниваем правые части уравнений:

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Источник

Чем меньше косинус тем больше угол

ИЗМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.

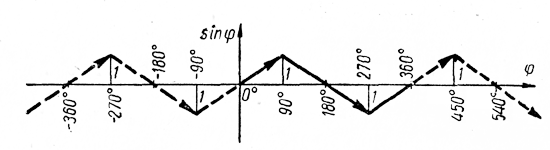
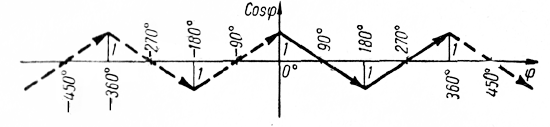
Изменение функций sin φ и cos φ
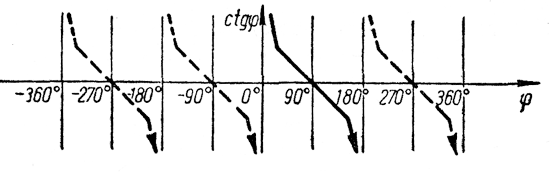
Изменение функций tg φ и ctg φ

Изменение функций sin φ и cos φ

Используя тригонометрический круг, выясним, как с изменением аргумента φ изменяются функции sin φ и cos φ.

Изменение функции sin φ

Пусть угол φ непрерывно возрастает от 0° до 90°. Тогда ордината соответствующего вектора будет непрерывно возрастать от 0 до 1. Следовательно, при увеличении угла от 0° до 90° синус его возрастает от 0 до 1.

Если угол φ непрерывно возрастает от 90° до 180°, то ордината соответствующего вектора будет непрерывно уменьшаться от 1 до 0. Следовательно, при увеличении угла φ от 90° до 180° синус его уменьшается от 1 до 0.

Из отмеченных выше свойств следует особо подчеркнуть следующее Свойство острых углов: чем больше острый угол, тем больше его синус. Так, sin 55° > sin 54°; sin 13° 56′ > sin 13°54′ и т. д.

Это утверждение, верное для острых углов, не распространяется на произвольные углы. Например, угол в 180° больше угла в 0°. Однако sin 180° = sin 0° = 0.

Аналогично тому, как мы изучили функцию sin φ, может быть рассмотрена и функция cos φ.

Изменение функции cos φ

При увеличении угла от 0° до 90° косинус его уменьшается от 1 до 0; при увеличении угла от 90° до 180° косинус его уменьшается от 0 до —1; при увеличении угла от 180° до 270° косинус его увеличивается от —1 до 0; при увеличении угла от 270° до 360° косинус его увеличивается от 0 до 1.

Косинусы углов, оканчивающихся в 1-й или в 4-й четвертях, положительны; косинусы углов, оканчивающихся во 2-й или в 3-й четвертях, отрицательны.

Следует особо подчеркнуть следующее свойство косинусов острых углов: чем больше острый угол, тем меньше его косинус. Так, cos 55° cos 180° (0 > —1).

1. Определить знаки следующих выражений:

1) sin 153°; 4) sin (—402°); 7) cos (— 1230°);

2) sin 273°; 5) cos 73°; 8) cos 140°;

3) sin 301°; 6) sin 910°; 9) sin 1000° · cos 1000°.

2. Доказать неравенства:

1) sin 61° > sin 60°; 5) cos 79° cos 150° ;

3) sin 196° > sin 201°; 7) cos 190° 0; б) sin φ cos φ 0, sin 2φ 0?

6. В каких четвертях может оканчиваться угол а, если:

7. Расположить в порядке возрастания величины;

а) sin (—55°); sin 600°; sin 1295°;
б) cos 654°; cos (—67°); cos 295°.

8.Как изменяется sin 2φ при изменении угла φ:

а) от 0° до 45°; и) от 135° до 180°;

б) от 90° до 135° ; г) от 5760° до 5805°?

9. Как изменяется cos 3φ при изменении угла φ от 3660° до 3690°?

Изменение функций tg φ и ctg φ

Изменение функций tg φ

При φ = ±90° tg φ не определен. Но если угол φ, оставаясь в пределах от —90° до 90°, хоть немного отличается от ±90°, то выражение tg φ уже определено. Посмотрим, как же ведет себя функция tg φ, когда ее аргумент φ близок к ± 90°.

По мере того как угол φ приближается к 90°, оставаясь меньше 90°, ордината соответствующей точки на оси тангенсов неограниченно возрастает.

(читается: предел тангенса φ, когда φ стремится к —90°, оставаясь при этом больше — 90°, равен минус бесконечности).

Мы исследовали поведение функции tg φ вблизи конечных точек интервала (—90°, 90°). Исследовать tg φ внутри этого интервала весьма просто. Как уже указывалось, tg φ может принимать любые числовые значения.

Из рисунка легко понять, что, чем больше значение аргумента φ в интервале (—90°, 90°), тем больше будет ордината соответствующей точки на оси тангенсов. Следовательно, из двух произвольных углов этого интервала большему соответствует больший тангенс.

Принято говорить, что
при увеличении угла от —90° до + 90° тангенс его возрастает от — ∞ до+ ∞

Схематично поведение функций tg φ в интервале—90° — 90°.

Изменение функций ctg φ

Аналогично можно исследовать и функцию ctg φ.

Схематично поведение функции ctgφ представлено на рисунке.

1. Определить знаки следующих выражений:

2. Какое число больше:

3. В каких четвертях может оканчиваться угол φ, если:

4. В каких четвертях имеют одинаковые знаки:

а) sin φ и tg φ; в) cos φ и tg φ;

б) cos φ и ctg φ; г) tg φ и ctg φ?

5. Какие пары тригонометрических функций имеют одинаковые знаки во всех четвертях?

6. Данные выражения расположить в порядке возрастания:

а) tg (—55°); tg 600°; tg 1295°;
б) ctg 295°; ctg (—67°); ctg 654°.

7. Какие тригонометрические функции внутреннего угла треугольника могут принимать отрицательные значения и когда именно?

8. Могут ли быть отрицательными значения тригонометрических функций:

а) половины внутреннего угла треугольника;
б) полусуммы двух внутренних углов треугольника;
в) полуразности двух внутренних углов треугольника?

Источник

Чем меньше косинус тем больше угол

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

В предыдущем уроке мы освоили базовые понятия. Это понятия тригонометрическая окружность, угол, синус и косинус этого угла. Освоили, что называется, «на пальцах». Главное сделано. Но чтобы толково использовать эти понятия на практике, надо чётко усвоить два момента.

1. Как считаются углы?
2. В чём они считаются?

Положительные и отрицательные углы в тригонометрии.

В этом небольшом уроке разберём первый вопрос.

Итак, как считать углы на тригонометрическом круге?
Смотрим на рисунок.

И добавлена зелёная стрелка. С плюсом. Что она означает? Напомню, что неподвижная сторона угла всегда прибита к положительной полуоси ОХ. Так вот, если подвижную сторону угла мы будем крутить по стрелке с плюсом, т.е. по возрастанию номеров четвертей, угол будет считаться положительным. Для примера на картинке показан положительный угол +60°.

Вот тут, обычно, начинаются первые непонятки. Как так!? А если отрицательный угол на круге совпадёт с положительным!? Да и вообще, получается что, одно и то же положение подвижной стороны (или точки на числовой окружности) можно обозвать как отрицательным углом, так и положительным!?

Зачем?! Как теперь считать углы, если можно и так и этак!? Как правильно!?

Не вопрос. Всяко правильно.) Выбор положительного или отрицательного исчисления угла зависит от условия задания. Если в условии ничего не сказано открытым текстом про знак угла, (типа «определить наименьший положительный угол» и т.д.), то работаем с удобными нам величинами.

Исключением (а как без них?!) являются тригонометрические неравенства, но там мы эту фишку освоим.

Углы больше 360°.

Зачем всё это нужно? Зачем нам переводить углы из одного в другой? Да всё за тем же.) С целью упрощения выражений. Упрощение выражений, собственно, главная задача школьной математики. Ну и, попутно, голова тренируется.)

Ну что, потренируемся?)

Отвечаем на вопросы. Сначала простые.

Есть проблемы? Или неуверенность? Идём в Раздел 555, Практическая работа с тригонометрическим кругом. Там, в первом уроке этой самой «Практической работы. » всё подробненько. В таких вопросах неуверенности быть не должно!

Всё нормально? Едем дальше:

Определили? Отлично! Сомневаетесь? Надо в Раздел 555. Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.

А теперь вопросы помудрёнее.

6. Привести выражение sin777° к синусу наименьшего положительного угла.

7. Привести выражение cos777° к косинусу наибольшего отрицательного угла.

8. Привести выражение cos(-777°) к косинусу наименьшего положительного угла.

9. Привести выражение sin777° к синусу наибольшего отрицательного угла.

Что, вопросы 6-9 озадачили? Привыкайте, на ЕГЭ и не такие формулировочки встречаются. Так и быть, переведу. Только для вас!

Ответы выдам по порядку (в нарушение наших правил). А что делать, знака всего два, а четверти всего четыре. Не разбежишься в вариантах.

В следующем уроке мы разберёмся с загадочными радианами и числом «Пи». Научимся легко и правильно переводить градусы в радианы и обратно. И с удивлением обнаружим, что этой элементарной информации на сайте уже хватает, чтобы решать некоторые нестандартные задачки по тригонометрии!

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Источник