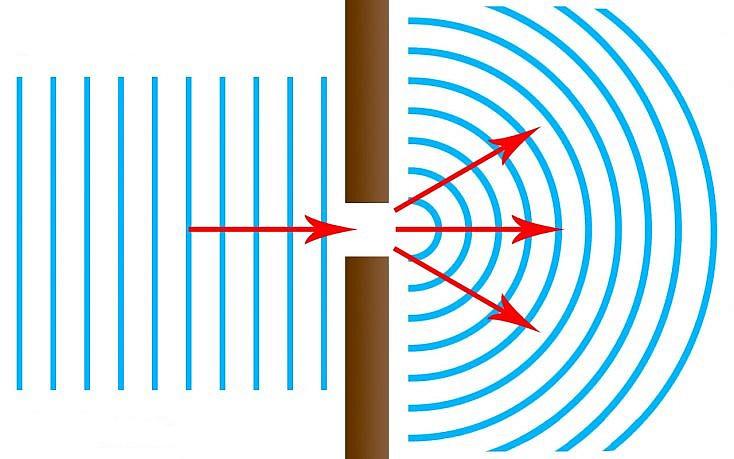
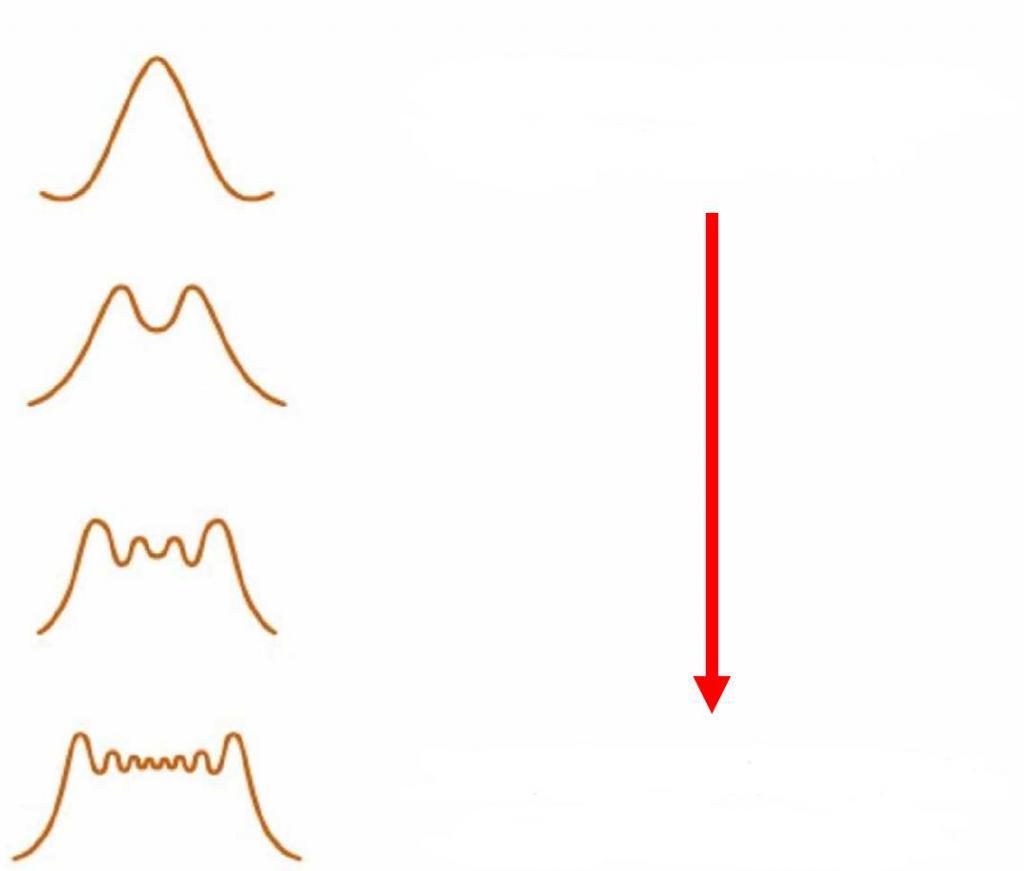
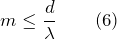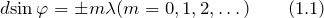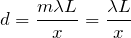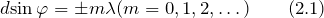Чем меньше период дифракционной решетки тем
Период дифракционной решетки
Определение и общие сведения о дифракционной решетке
Дифракционные решетки подразделяют на одномерные и многомерные. Одномерная дифракционная решетка состоит из параллельных прозрачных для света участков одинаковой ширины, которые располагаются в одной плоскости. Прозрачные участки разделяют непрозрачные промежутки. При помощи данных решеток наблюдения проводят в проходящем свете.
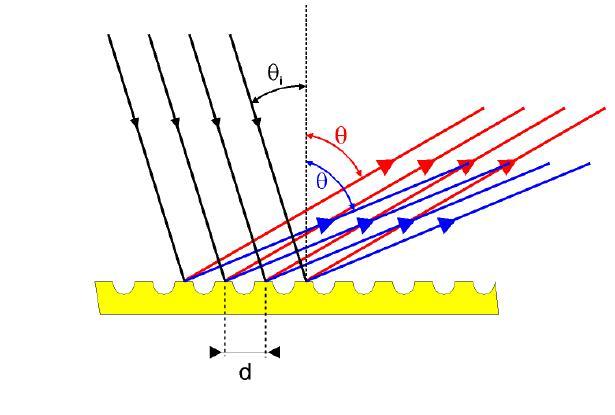
Существуют отражающие дифракционные решетки. Такая решетка представляет собой, например, полированную (зеркальную) металлическую пластинку, на которую нанесены штрихи при помощи резца. В результате получают участки, которые отражают свет и участки, которые свет рассеивают. Наблюдение при помощи такой решетки проводят в отраженном свете.
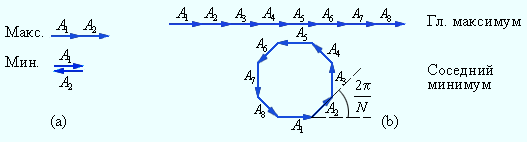
Картина дифракции на решетке — это результат взаимной интерференции волн, которые идут ото всех щелей. Следовательно, при помощи дифракционной решетки реализуется многолучевая интерференция когерентных пучков света, которые подверглись дифракции и которые идут от всех щелей.
Период дифракционной решетки
Если ширину щели на решетки обозначим a, ширину непрозрачного участка – b, тогда сумма данных двух параметров – это период решетки (d):
Период дифракционной решетки иногда называют еще постоянной дифракционной решетки. Период дифракционной решетки можно определить как расстояние, через которое происходит повтор штрихов на решетке.
Постоянную дифракционной решетки можно найти, если известно количество штрихов (N), которые имеет решетка на 1 мм своей длины:
Период дифракционной решетки входит в формулы, которые описывают картину дифракции на ней. Так, если монохроматическая волна падает на одномерную дифракционную решетку перпендикулярно к ее плоскости, то главные минимумы интенсивности наблюдаются в направлениях, определенных условием:
где 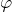
Кроме главных минимумов, в результате взаимной интерференции световых лучей, которые посылает пара щелей, в некоторых направлениях они гасят друг друга, в результате появляются дополнительные минимумы интенсивности. Они возникают в направлениях, где разность хода лучей составляют нечетное число полуволн. Условие дополнительных минимумов записывают как:
где N – число щелей дифракционной решетки; 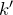
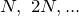
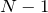
Условием главных максимумов для дифракционной решетки служит выражение:
Величина синуса не может превышать единицу, следовательно, число главных максимумов (m):
Примеры решения задач
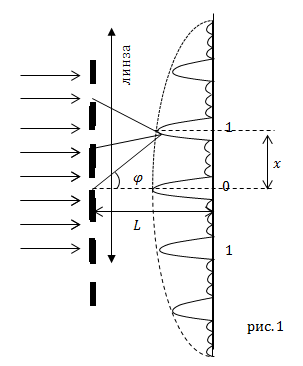
| Задание | Сквозь дифракционную решетку проходит пучок света, имеющий длину волны 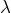 . На расстоянии L от решетки размещается экран, на который при помощи линзы формируют картину дифракции. Получают, что первый максимум дифракции расположен на расстоянии x от центрального (рис.1). Каков период дифракционной решетки (d)? . На расстоянии L от решетки размещается экран, на который при помощи линзы формируют картину дифракции. Получают, что первый максимум дифракции расположен на расстоянии x от центрального (рис.1). Каков период дифракционной решетки (d)? |
| Решение | Сделаем рисунок. |
В основу решения задачи положим условие для главных максимумов картины дифракции:
По условию задачи речь идет о первом главном максимуме, то 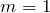
Из выражений (1.2) и (1.1) имеем:
Выразим искомый период решетки, получаем:
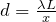
| Задание | Каков период дифракционной решетки (d), если углу дифракции 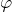 будет соответствовать максимум k-го порядка? Длина волны света, падающего на дифракционную решетку равна будет соответствовать максимум k-го порядка? Длина волны света, падающего на дифракционную решетку равна 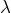 . . |
| Решение | Условием главных максимумов для дифракционной решетки служит выражение: |
По условию 
Дифракционная решетка. Постоянная и период решетки. Использование в спектроскопии
Дифракционная решетка часто используется для определения спектра падающего на нее света, поскольку она позволяет расщеплять его на отдельные цвета. В данной статье рассмотрим, что такое дифракционная решетка, постоянная и период ее, и приведем пример решения задачи с использованием этого оптического прибора.
Явление дифракции
Суть его заключается в изменении направления распространения волны, когда она встречает на своем пути препятствие. Результат дифракции хорошо различим, если размеры препятствия сравнимы с длиной волны или меньше нее. Дифрагированная волна способна проникать в области за препятствием, куда она не смогла бы попасть, если бы двигалась вдоль прямой.

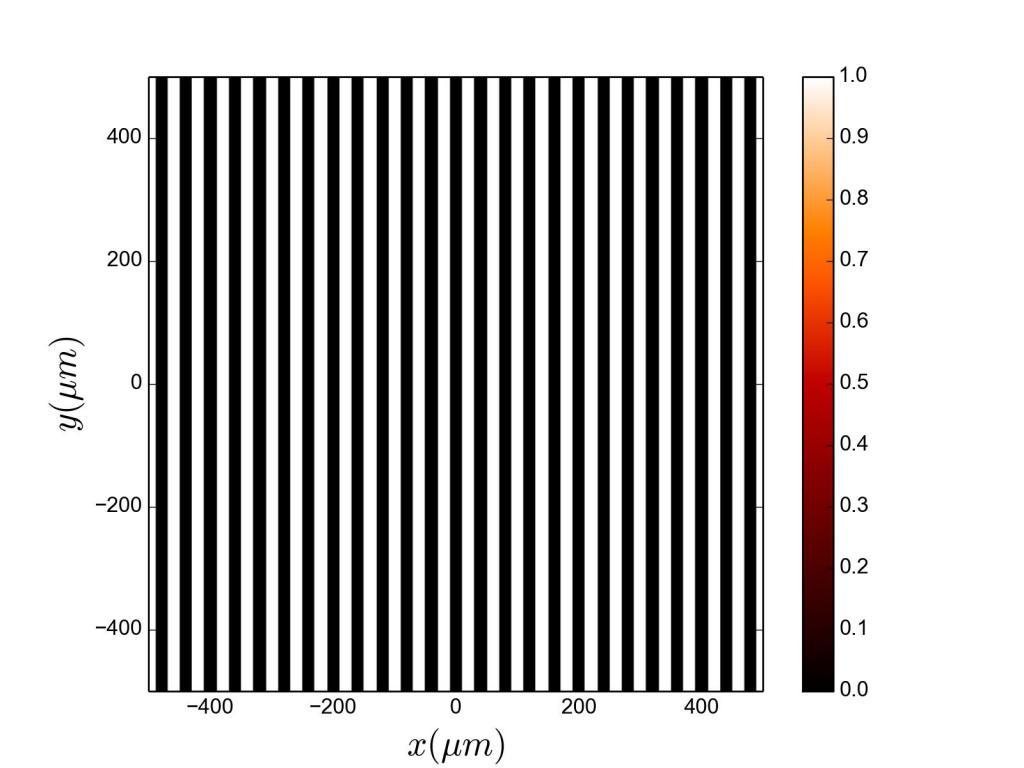
На рисунке ниже приведен пример дифракции морской волны.
Видно, как прямой фронт волны после прохождения препятствия приобретает форму окружности.
Математическое описание дифракции осуществляется с использованием принципа Гюйгенса-Френеля, который гласит, что каждая точка волнового фронта является источником вторичной волны некоторой интенсивности.
Дифракция часто сопровождается интерференцией. Благодаря этим двум явлениям можно наблюдать так называемые дифракционные картины.
Дифракционная решетка
Это решетка представляет собой прозрачную пластинку, на которую нанесены непрозрачные штрихи с определенным периодом. Когда свет проходит через такую пластинку, то она вносит периодическое возмущение в его волновой фронт. В результате возникает ряд вторичных источников, которые испускают когерентные волны. В результате интерференции когерентные волны образуют на экране совокупность максимумов и минимумов, то есть дифракционную картину.
Описанная выше решетка называется проходящей или прозрачной. Существует также отраженная дифракционная решетка, которая представляет собой совокупность периодических бороздок, нанесенных на гладкую поверхность материала. Примером этого вида решетки является DVD-диск.
Уравнение решетки
В приближении дальнего поля (дифракция Фраунгофера) уравнение для решетки выглядит следующим образом:
Приведенная формула непосредственно следует из условия интерференционного максимума. В лабораторных работах ее используют для определения либо постоянной дифракционной решетки, когда λ известна, либо длины волны, когда d известен.
Использование дифракционной решетки в спектроскопии
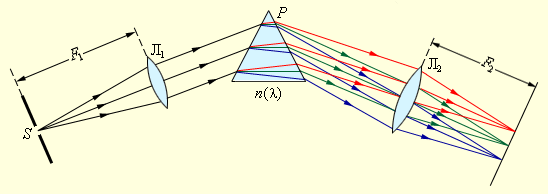
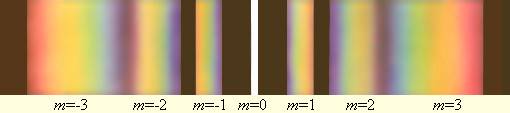
Приведенное выше уравнение решетки позволяет сделать вывод, что углы θm, в которых появляются максимумы, зависят от длины волны. Чем больше она, тем больше эти углы (длинные волны лучше дифрагируют, чем короткие). Это означает, что если на решетку направить белый свет, то она его разложит на ряд цветов подобно дисперсионной призме. Причем последовательность цветов, начиная от центра (m=0), будет идти от фиолетового к красному.
Каждый максимум для соответствующего порядка дифракции и белого света будет представлять собой «радугу». Единственным максимумом, который всегда будет белым, является центральный или нулевой (m=0).
Явление разложения белого света на отдельные составляющие позволяет использовать дифракционную решетку в спектроскопии. Например, пропуская свет от далекой галактики через решетку, а затем анализируя полученный спектр, можно с достоверностью сказать, какие элементы присутствуют в галактике, какая у них температура, с какой скоростью движется эта галактика относительно нас (в последнем случае учитывается эффект Доплера).
Пример решения задачи
Покажем, как пользоваться уравнением решетки, на примере решения простой задачи. Пусть постоянная дифракционной решетки равна 300 штрихов на 1 мм. Необходимо определить, при каком угле будет наблюдаться максимум первого порядка для фиолетовой (400 нм) и для красной (700 нм) волн.
Учитывая, что число штрихов N обратно пропорционально периоду d, перепишем уравнение решетки в виде:
Угол для первого максимума равен:
Подставляем данные в единицах СИ в это выражение, получаем:
Для фиолетового: θ1 = arcsin(400*10-9*300*103) = 6,89o.
Для красного: θ1 = arcsin(700*10-9*300*103) = 12,12o.
Если экран поставить на расстоянии 1 метра от решетки, тогда на нем красная и фиолетовая полосы для первого порядка дифракции будут находиться на расстоянии около 9 см друг от друга.
Дифракционная решётка
Дифракционная решётка – это прибор в оптическом устройстве, который основан на явлении дифракции. Она представляет собой множество узких щелей, разделённых непрозрачными промежутками.
Пусть ширина прозрачных щелей равна а, ширина непрозрачных промежутков равна b. Тогда введём величину d=a+b. Назовём её периодом решётки. Как правило, период решётки колеблется в районе 10 мкм.
Теория дифракционной решётки
Сформулируем теорию дифракционной решётки. Предположим, что на решётку попадает плоская монохроматическая волна с некоторой длиной волны λ. Учтём, что период оптического устройства мал и, соответственно, пучок будет огибать непрозрачные промежутки.
Вспомним принцип Гюйгенса, согласно которому вторичные когерентные источники, локализующиеся в щелях, генерируют световые пучки, которые распространяются равномерно по всем направлениям.
Теперь найдём условие максимума, то есть случай, при котором идущие от щелей волны взаимно усиливают друг друга.
Рассмотрим ситуацию, когда волны распространяются в направлении, которое определяется углом ϕ.
Отрезок АС – это разность хода волн между соседними щелями. Пусть на этом промежутке укладывается целое число длин волн. Тогда волны будут складываться между собой. Из треугольника АВС можно найти катет АС. Он будет равен: АС=АВsinϕ=dsinϕ. При этом наглядно видно, что максимумы наблюдаются под углом ϕ при следующих условиях: dsinϕ=±kλ, где k=0, 1,2,… Углы ϕ, которые удовлетворяют этому условию определяют положения главных максимумов.
Важно учитывать, что за взаимное усиление отвечают не только волны от нижних краёв щели, но и от всех других точек отверстия. Если взять две щели, то каждая точка в первой щели будет иметь идентичную точку на второй.
Теперь поместим за дифракционной решёткой собирающую линзу, а за линзой – экран на фокусном расстоянии. Рассмотрим движение светового пучка. Лучи попадают на линзу, которая собирает их в одной точке. В этой же точке происходит взаимное сложение волн. Следовательно, происходит усиление амплитуды.
Проводя такой эксперимент, мы получаем ещё и дифракционные картины отдельных щелей, а не только их совокупности. Нетрудно догадаться, что интенсивность максимумов в одном элементе дифракционной решётки значительно меньше интенсивности главных максимумов всей системы.
Порядок спектра k имеет особый смысл в теории дифракционной решётки. Чем больше число щелей, тем лучше видны максимумы, которые разделены между собой широкими минимумами.
Энергия на дифракционной решётке
Когда световой пучок падает на дифракционную решётку, то энергия, переносимая им, перераспределяется таким образом, что большая её доля выделяется под максимумы. В минимумы же попадают лишь остатки этой энергии.
Применение дифракционной решётки
Дифракционная решётка нужна для измерения длины волны. Если нам известен период решётки, то для определения длины волны достаточно найти угол ϕ.
Чтобы наблюдать дифракционную картину, необходимо взять яркий источник света и посмотреть на него, прищурив глаза. Мы увидим радужные переливы, которые создают наши ресницы. А наши ресницы, по сути, это грубое представление дифракционной решётки в оптическом устройстве.
Основная формула дифракционной решетки
В чем заключаются явления дифракции и интерференции?
Прежде чем рассматривать вывод формулы дифракционной решетки, следует познакомиться с явлениями, благодаря которым это решетка оказывается полезной, то есть с дифракцией и интерференцией.
Оба описанных явления впервые объяснил англичанин Томас Юнг, когда исследовал дифракцию монохроматического света на двух тонких щелях в 1801 году.
Принцип Гюйгенса-Френеля и приближения дальнего и ближнего полей
Математическое описание явлений дифракции и интерференции является нетривиальной задачей. Нахождение точного ее решения требует выполнение сложных расчетов с привлечением максвелловской теории электромагнитных волн. Тем не менее в 20-е годы XIX века француз Огюстен Френель показал, что, используя представления Гюйгенса о вторичных источниках волн, можно с успехом описывать эти явления. Эта идея привела к формулировке принципа Гюйгенса-Френеля, который в настоящее время лежит в основе вывода всех формул для дифракции на препятствиях произвольной формы.
Тем не менее даже с помощью принципа Гюйгенса-Френеля решить задачу дифракции в общем виде не удается, поэтому при получении формул прибегают к некоторым приближениям. Главным из них является плоский волновой фронт. Именно такая форма волны должна падать на препятствие, чтобы можно было упростить ряд математических выкладок.
Следующее приближение заключается в положении экрана, куда проецируется дифракционная картина, относительно препятствия. Это положение описывается числом Френеля. Оно вычисляется так:
Разница между дифракциями Фраунгофера и Френеля заключается в различных условиях для явления интерференции на маленьком и большом расстояниях от препятствия.
Вывод формулы главных максимумов дифракционной решетки, который будет приведен далее в статье, предполагает рассмотрение дифракции Фраунгофера.
Дифракционная решетка и ее виды
Существует два типа дифракционных решеток:
Какой бы ни был тип решетки, идея ее воздействия на волновой фронт заключается в создании периодического возмущения в нем. Это приводит к образованию большого количества когерентных источников, результатом интерференции которых является дифракционная картина на экране.
Основная формула дифракционной решетки
Вывод этой формулы предполагает рассмотрение зависимости интенсивности излучения от угла его падения на экран. В приближении дальнего поля получается следующая формула для интенсивности I(θ):
I(θ) = I0*(sin(β)/β)2*[sin(N*α)/sin(α)]2, где
Пользуясь приведенной формулой, можно рассчитать значение интенсивности для любого угла падения света.
Если находить значение максимумов интенсивности I(θ), то можно прийти к выводу, что они появляются при условии, что α = m*pi, где m является любым целым числом. Для условия максимумов получаем:
Другие способы записи основной формулы для решетки
Заметим, что в приведенной в предыдущем пункте формуле присутствует член sin(θ0). Здесь угол θ0 отражает направление падения фронта световой волны относительно плоскости решетки. Когда фронт падает параллельно этой плоскости, то θ0 = 0o. Тогда получаем выражение для максимумов:
Поскольку постоянная решетки a (не путать с шириной щели) обратно пропорциональна величине d, то через постоянную дифракционной решетки формула выше перепишется в виде:
Чтобы не возникало ошибок при подстановке конкретных чисел λ, a и d в эти формулы, следует всегда использовать соответствующие единицы СИ.
Понятие об угловой дисперсии решетки
Будем обозначать эту величину буквой D. Согласно математическому определению, она записывается следующим равенством:
Физический смысл угловой дисперсии D заключается в том, что она показывает, на какой угол dθm сместится максимум для порядка дифракции m, если изменить длину падающей волны на dλ.
Если применить это выражение для уравнения решетки, тогда получится формула:
Дисперсия угловая дифракционной решетки определяется по формуле выше. Видно, что величина D зависит от порядка m и от периода d.
Чем больше дисперсия D, тем выше разрешающая способность данной решетки.
Разрешающая способность решетки
Под разрешающей способностью понимают физическую величину, которая показывает, на какую минимальную величину могут отличаться две длины волны, чтобы их максимумы на дифракционной картине появлялись раздельно.
Разрешающая способность определяется критерием Рэлея. Он гласит: два максимума можно разделить на дифракционной картине, если расстояние между ними оказывается больше полуширины каждого из них. Угловая полуширина максимума для решетки определяется по формуле:
Разрешающая способность решетки в соответствии с критерием Рэлея равна:
Δθm>Δθ1/2 или D*Δλ>Δθ1/2.
Подставляя значения D и Δθ1/2, получаем:
Это и есть формула разрешающей способности дифракционной решетки. Чем больше число штрихов N на пластинке и чем выше порядок дифракции, тем больше разрешающая способность для данной длины волны λ.
Дифракционная решетка в спектроскопии
Выпишем еще раз основное уравнение максимумов для решетки:
Здесь видно, что чем больше длина волны падает на пластинку со штрихами, тем при больших значениях углов будут появляться максимумы на экране. Иными словами, если через пластинку пропустить немонохроматический свет (например, белый), то на экране можно видеть появление цветных максимумов. Начиная от центрального белого максимума (дифракция нулевого порядка), дальше будут появляться максимумы для более коротких волн (фиолетовый, синий), а затем для более длинных (оранжевый, красный).
Другой важный вывод из этой формулы заключается в зависимости угла θm от порядка дифракции. Чем больше m, тем больше значение θm. Это означает, что цветные линии будут сильнее разделены между собой на максимумах для высокого порядка дифракции. Этот факт уже был освящен, когда рассматривалась разрешающая способность решетки (см. предыдущий пункт).
Описанные способности дифракционной решетки позволяют использовать ее для анализа спектров излучения различных светящихся объектов, включая далекие звезды и галактики.
Пример решения задачи
Покажем, как пользоваться формулой дифракционной решетки. Длина волны света, которая падает решетку, равна 550 нм. Необходимо определить угол, при котором появляется дифракция первого порядка, если период d равен 4 мкм.
Угол θ1 легко рассчитать по формуле:
Переводим все данные в единицы СИ и подставляем в это равенство:
θ1 = arcsin(550*10-9/(4*10-6)) = 7,9o.
Если экран будет находиться на расстоянии 1 метр от решетки, то от середины центрального максимума линия первого порядка дифракции для волны 550 нм появится на расстоянии 13,8 см, что соответствует углу 7,9o.
Спектральные приборы. Дифракционная решетка
В состав видимого спектра света включены монохроматические волны с различными длинами. В излучении нагретых объектов (к примеру, нити лампы накаливания) длины волн беспрерывно заполняют весь диапазон видимого света. Данное излучение называют белым светом.
Свет, излучаемый, например, газоразрядными лампами или одним из множества других подобных им приборами, включает в свой состав отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн.
Комплекс монохроматических компонент в излучении называется спектром.
Белый свет имеет непрерывный спектр, излучение источников, в которых он испускается атомами вещества, и дискретный спектр.
Спектральные приборы – это устройства, с помощью которых изучаются спектры излучения источников.
Первый опыт по разложению белого света в спектр осуществил известный физик И. Ньютон в 1672 году.
Дифракционные решетки
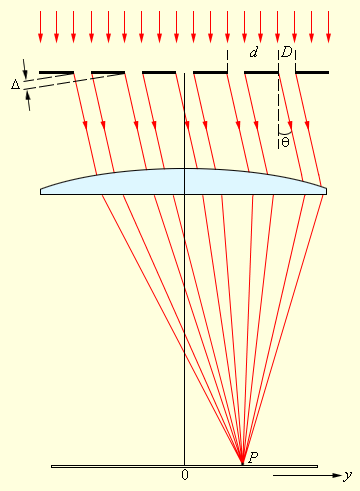
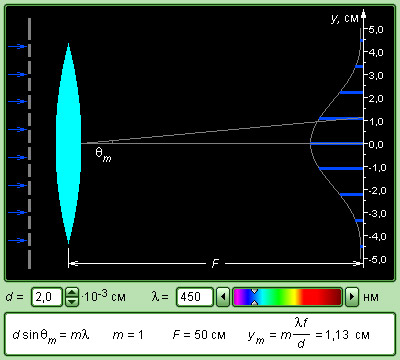
В каждой точке P на экране в фокальной плоскости линзы сходятся лучи, который до линзы являлись параллельными между собой и расходились под некоторым углом θ к направлению падающей волны.
Интерференция волн
Колебание в точке P представляют собой следствие интерференции вторичных волн, которые сходятся в эту точку от разных щелей.
Для того, чтобы в точке P прослеживался интерференционный максимум, разность хода Δ между волнами, который испускают соседние щели, должна быть эквивалентной целому числу длин волн:
Где d – это период дифракционной решетки, а m – целое число, носящее название порядка дифракционного максимума. В точках экрана, для которых это условие выполнено, расположены главные максимумы дифракционной картины.
где F – фокусное расстояние.
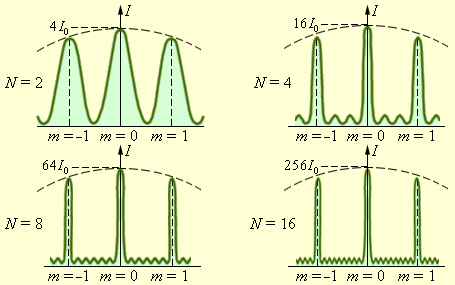
Также следует обратить внимание на то, что в каждой точке фокальной плоскости линзы, имеет место интерференция N волн, которые приходят в эту точку от N щелей решетки. Данный феномен является так называемой многоволновой или же «многолучевой» интерференцией.
Распространение световой энергии в плоскости наблюдения значительно отличается от того, которое выходит в обыкновенных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, из-за чего амплитуда колебаний увеличивается в N раз, а интенсивность в N 2 раз, относительно колебания, которое провоцирует волна только от одной конкретной щели.
Здесь, дифракционные углы считаются достаточно малыми. Таким образом,
Где N d – это полный размер решетки. Данное выражение находится в полной симметрии с теорией дифракции в параллельных лучах. Согласно этой теории, дифракционная расходимость параллельного пучка лучей эквивалентна отношению длины волны λ к поперечному размеру препятствия.
Волновая природа света
Волновая природа света определяет разрешающую способность спектральных приборов, в частности, дифракционной решетки, так же от нее зависит предельное разрешение различных оптических инструментов, которые создают изображение объектов, таких как телескоп, микроскоп и др.
Из формулы решетки следует:
d d · cos θ · ∆ θ = m ∆ λ или ∆ θ = m δ cos θ ∆ λ ≈ m d ∆ λ