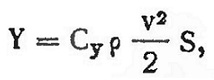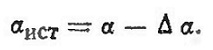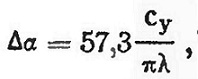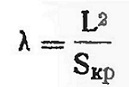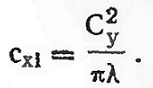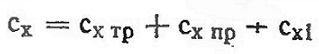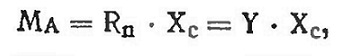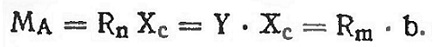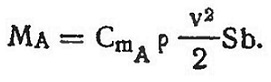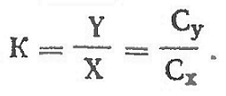Чем меньше скорость тем меньше давление

ЧАРУЮЩИЕ ТАЙНЫ ЖИДКОСТИ

Доктор физико-математических наук А. МАДЕРА

ПОСТОЯНСТВО ПОТОКА МАССЫ ЖИДКОСТИ

Его еще называют законом неразрывности, законом непрерывности, уравнением сплошности жидкости или законом сохранения вещества в гидродинамике. По существу, этот закон был открыт Б. Кастелли в 1628 году. Он установил, что скорость течения жидкости в трубах обратно пропорциональна площади их поперечного сечения. Другими словами, чем уже сечение канала, тем с большей скоростью движется в нем жидкость.

И. Ньютон (конец XVII века) экспериментально установил, что любой жидкости свойственна вязкость, то есть внутреннее трение. Вязкость приводит к возникновению сил трения между движущимися с различными скоростями слоями жидкости, а также между жидкостью и омываемым ею телом. Им же было установлено, что сила трения пропорциональна коэффициенту вязкости жидкости и градиенту (перепаду) скорости потока в направлении, перпендикулярном его движению. Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.

В силу вязкого трения скорость жидкости на поверхности омываемого ею тела всегда равна нулю. Это совсем не очевидно, но тем не менее подтверждается во множестве экспериментов.

Опыт. Убедимся, что скорость газа на поверхности обдуваемого им тела равна нулю.

Возьмем вентилятор и припудрим его лопасти пылью. Включим вентилятор в сеть и через несколько минут выключим. Пыль на лопастях как была, так и осталась, хотя вентилятор вращался с довольно большой скоростью и она должна была бы слететь.

Омывая лопасти вентилятора с большой скоростью, поток воздуха на их поверхности имеет нулевую скорость, то есть неподвижен. Поэтому пыль на них и остается. По этой же причине с гладкой поверхности стола легко можно сдуть крошки, а пыль приходится вытирать.

#1# ИЗМЕНЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В ЗАВИСИМОСТИ ОТ СКОРОСТИ ЕЕ ДВИЖЕНИЯ.

Это уравнение играет фундаментальную роль в гидродинамике, несмотря на то, что оно, строго говоря, справедливо только для идеальной, то есть не имеющей вязкости, жидкости.

Опыт 1. Убедимся, что чем выше скорость воздуха, тем меньше давление в нем.

Зажжем свечу и через тонкую трубочку, например для коктейля, сильно дунем в нее так, чтобы струйка воздуха прошла примерно на расстоянии 2 см от пламени. Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.

#3# Лабораторный водоструйный насос. В струе воды из крана создается разрежение, которое выкачивает воздух из колбы.

Почему? Согласно уравнению Бернулли, чем выше скорость потока, тем меньше давление в нем. Воздух выходит из трубочки с большой скоростью, так что давление в струе воздуха меньше, чем в окружающем свечу неподвижном воздухе. Перепад давления при этом направлен в сторону выходящего из трубочки воздуха, что и отклоняет к ней пламя свечи.

#4# Принцип работы пульверизатора: атмосферное давление выжимает жидкость в струю воздуха, где давление ниже.

На этом принципе работают пульверизаторы, струйные насосы и автомобильные карбюраторы: жидкость втягивается в поток воздуха, давление в котором ниже атмосферного.

Опыт 2. Возьмем лист писчей бумаги за верхние края, поднесем его к стене и удержим на расстоянии примерно 3-5 см от стены. Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.

#6# СОПРОТИВЛЕНИЕ, ИСПЫТЫВАЕМОЕ ТЕЛОМ ПРИ ДВИЖЕНИИ В ЖИДКОСТИ

Необходимо отметить, что сопротивление жидкости движущемуся в нем телу в значительной мере обусловливается именно наличием вязкости. В идеальной жидкости, в которой вязкость отсутствует, сопротивление вообще не возникает.

Возьмем свечу и коробок спичек. Зажжем свечу, поставим перед ней на расстоянии примерно 3 см коробок и сильно дунем на него. Пламя свечи отклоняется к коробку. Это означает, что позади коробка давление стало меньше, чем позади свечи, и разность давлений направлена по движению потока воздуха. Следовательно, тело при движении в воздухе или жидкости испытывает торможение.

Поток воздуха набегает на переднюю поверхность коробка, огибает его по краям и не смыкается позади, а отрывается от препятствия. Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен. Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.

Сопротивление зависит от скорости движения тела в жидкости, свойств жидкости, формы тела и его размеров. Важную роль в создании сопротивления играет форма задней стороны движущегося тела. Позади плоского тела возникает пониженное давление, поэтому сопротивление можно уменьшить, предотвратив срыв потока. Для этого телу придают обтекаемую форму. Поток плавно огибает тело и смыкается непосредственно за ним, не создавая области пониженного давления.

Опыт 2. Чтобы продемонстрировать различный характер обтекания, а следовательно, и сопротивле ния тел различной формы, возьмем шар, например мяч для пинг-понга или тенниса, приклеим к нему бумажный конус и поставим за ним горящую свечу.

ПАДЕНИЕ ДАВЛЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ ПРИ ЕЕ ДВИЖЕНИИ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ

Опыт показывает, что давление в жидкости, текущей по трубе постоянного сечения, падает вдоль трубы по течению: чем дальше от начала трубы, тем оно ниже. Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.

Опыт. Возьмем резиновую или пластиковую трубку постоянного сечения и такого диаметра, чтобы ее можно было насадить на носик водопроводного крана. Сделаем в трубке два отверстия и откроем воду. Из отверстий начнут бить фонтанчики, причем высота ближнего к крану фонтанчика будет заметно выше, чем расположенного дальше по потоку. Это показывает, что давление воды в ближайшем к крану отверстии выше, чем в дальнем: оно падает вдоль трубы в направлении потока.

Объяснение этого явления на молекулярном уровне автору не известно. Поэтому приведем классическое объяснение. Выделим в жидкости маленький объем, ограниченный стенками трубки и двумя сечениями слева и справа. Так как жидкость течет по трубке равномерно, то разность давлений слева и справа от выделенного объема должна быть уравновешена силами трения между жидкостью и стенками трубки. Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.

На первый взгляд приведенное объяснение удовлетворительно. Однако возникают вопросы, ответа на которые пока нет.

Итак, налицо экспериментальный факт, который легко проверить, однако объяснение его остается открытым.

Речь идет о возникновении силы, перпендикулярной потоку жидкости при обтекании ею вращающегося тела. Этот эффект был обнаружен и объяснен Г. Г. Магнусом (около середины XIX столетия) при изучении полета вращающихся артиллерийских снарядов и их отклонения от цели. Эффект Магнуса состоит в следующем. При вращении летящего тела близлежащие слои жидкости (воздуха) увлекаются им и также получают вращение вокруг тела, то есть начинают циркулировать вокруг него. Встречный поток рассекается телом на две части. Одна часть направлена в ту же сторону, что и циркулирующий вокруг тела поток; при этом происходит сложение скоростей набегающего и циркулирующего потоков, значит, давление в этой части потока уменьшается. Другая часть потока направлена в сторону, противоположную циркуляции, и здесь результирующая скорость потока падает, что приводит к увеличению давления. Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).

Опыт. Склеим из листа плотной бумаги цилиндр. Из доски, положенной одним краем на стопку книг, сделаем на столе наклонную плоскость и положим на нее цилиндр. Скатившись, он вроде бы должен дальше двигаться по параболе и упасть дальше от края. Однако вопреки ожидаемому траектория его движения загибается в другую сторону, и цилиндр залетает под стол. Все дело в том, что он не просто падает, а еще и вращается, создавая вокруг себя циркуляцию воздуха. Возникает избыточное давление, направленное в сторону, противоположную поступательному движению цилиндра.

ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ ПОТОКИ

Опыт обнаруживает две совершенно разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.

#12# Струя воды падает в поле тяжести, испытывая ускорение. Как только скорость течения возрастает настолько, что число Рейнольдса превышает критическое значение, ламинарное течение (вверху) переходит в турбулентное. Для данного течения Re»2300.

Источник

Закон Бернулли для чайников и учёных

Предисловием можно считать «За что физики не любят математиков»: http://proza.ru/2015/11/16/160

«Наука должна быть весёлая, увлекательная и простая. Таковыми же должны быть и учёные» (П.Л. Капица). и преподаватели. Но более всего наука должна быть честная. И «Ни один человек не должен покидать стены наших университетов без понимания того, как мало он знает» (Роберт Оппенгеймер). и как мало знают учёные. А чтобы так оно и было, нужно срезать профессора математической лженауки на первой же лекции. И прежним занудой он уже не будет. Знаю, что говорю, и привожу очередной пример.

Правильный ответ: неподвижные поверхностные манометры на картинке вверху показывают давление потоков, так как для измерения давления в потоках нужны такие манометры или датчики давления, которые находились бы внутри потоков и двигались вместе с ними. Давление внутри потоков, знаете ли, почти всегда статично. Но таких мобильных манометров, которые могли бы быть неподвижными относительно ламинарных потоков, нет в опытах к теме «Закон Бернулли». Однако вывод сделан такой, словно они есть, словно давление внутри потоков уже измерено. «Для физика должно существовать только то, что измерено» (Нильс Бор). а не то, что можно подумать, придумать, недодумать и сосчитать. Сосчитать то, чего нет, может каждый.

А тем-то он и хуже, что никакой научности и сложности для понимания в нём нет. К тому же, давление потока на поперечную поверхность или «скоростной напор» измеряется с помощью Г-образной «трубки Пито», вставляемой в поток загнутым концом навстречу потоку. Отсюда: давление в самом потоке примерно равно среднему арифметическому от показаний «трубки Пито» и «трубки у Бернулли». Более того, в ньютоновской механике уменьшение силы давления на параллельную потоку или телу поверхность с увеличением скорости потока или тела и одновременное увеличение давления потока или тела на поперечную поверхность можно объяснить простым векторным разложением силы давления потока или тела. Чем больше скорость автомобиля, тем меньше его вес и давление на дорожное полотно; чем больше скорость потока, тем меньше его давление на стенки трубы. Пусть пока будет так.

Конечно, наши выводы профессору будут сильно не по нутру. Но если он будет ещё в состоянии что-то говорить и продолжит настаивать на том, что «С увеличением скорости потока давление внутри потока уменьшается», то срежем его вторым вопросом: «Почему причина и следствие в формулировке общепризнанного закона Бернулли переставлены местами?».

Можно короче: «Чем больше падение давления в потоке или на данном участке трубы, тем больше здесь и скорость самого потока». И это будет тривиальный закон потоков, у которого уже есть все пять обязательных признаков новой истины: простота, ясность, универсальность, «предсказательная сила» и антинаучность. Опровергнуть этот закон сможет только тот, кто создаст поток жидкости или газа, движущийся из области пониженного давления в область повышенного давления, то есть против действия превосходящих сил давления и упругости. Шутка.

Инженер-аэродинамист сформулирует свой закон потоков примерно так: «Давление потока на параллельную или отрицательно наклонную поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока или поверхности (верхней поверхности крыла); а давление потока на поперечную или положительно наклонную поверхность всегда тем больше давления в самом потоке, чем больше скорость потока или поверхности (нижней поверхности атакующего крыла)». И это будет качественный закон взаимодействия потоков с поверхностями, так как в каждом конкретном случае величина давления потока на поверхность зависит не только от скорости потока, но и от физических свойств потока и поверхности, поэтому она не вычисляется, а только измеряется. Следовательно, математикам и в аэродинамике делать особо нечего.

Действие этих двух законов во многих опытах и явлениях складывается или накладывается, поэтому наблюдаемый результат нельзя объяснять действием только какого-то одного закона. Но объединённого закона Бернулли или третьего математического закона потоков никогда не было, поэтому как определить «личную долю» каждого закона в результате того или иного опыта к теме «Закон Бернулли» не знает ни один математик. но знает каждый инженер. Он просто измеряет с помощью манометров и динамометров давление в потоке и давление потока при различной скорости потока, а потом лишь сравнивает результаты измерений. и никаких теорий потоков для него словно не существует. Действительно, зачем вычислять, если можно измерить.

Качественный закон потоков гласит: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». Можно короче: «Давление потока на параллельную поверхность всегда тем меньше, чем больше хаос в движении частиц потока».

В гидродинамике давление всегда первично, а скорость потока вторична; в аэродинамике скорость крыла всегда первична, а давление неподвижной атмосферы на него всегда вторично. Плоское крыло самолёта или птицы не изменяет давление в неподвижной атмосфере, а изменяется с увеличением скорости и угла атаки лишь взаимодействие быстрого крыла с атмосферой. Но в наших рассуждениях крыло чаще всего неподвижно, а это атмосфера «набегает» на крыло, словно всё происходит в аэродинамической трубе или в статическом (стационарном) потоке. Просто так нам удобнее рассуждать и объяснять.

У инженеров всё, что летает, делает это по причине совсем небольшой положительной разницы или асимметрии атмосферного давления на крыло. Появление подъёмной силы как раз и обусловлено качественным законом потоков: «Давление атмосферного потока на верхнюю отрицательно наклонную поверхность быстрого крыла тем меньше давления в самой атмосфере, чем больше хаос и разрежение частиц воздуха над ней; а давление потока на нижнюю положительно наклонную поверхность крыла тем больше атмосферного давления, чем больше скорость крыла, его угол наклона или атаки и деформация или уплотнение упругого воздуха под быстрым крылом». Как диагональ делит прямоугольник на два равных треугольника, так и плоское атакующее крыло делит набегающий поток на две самостоятельные и равнозначные причины возникновения подъёмной силы.

Вспомним, атмосферное давление на уровне моря равно 1,0033 кг/см2. Это очень большая сила, которая давит на неподвижное плоское крыло совершенно одинаково и сверху, и снизу. Если атмосферное давление со стороны одной из поверхностей крыла убрать, то со стороны противоположной поверхности тут же возникнет сила равная 10033 кг/м2. Да, 10 тонн на каждый квадратный метр крыла! И что мы имеем: орёл весом 4 кг, имея площадь «несущих поверхностей» как раз 1м2, почти неподвижно парит в вышине при положительной разнице атмосферных давлений на его крылья всего 0,04% от теоретически возможного 1 кг/см2; АН-2 («кукурузник») летает горизонтально на разности 0,4% атмосферного давления; а скоростному современному пассажирскому авиалайнеру для горизонтального полёта достаточно и 5% от 1 кг/см2 или 50 г/см2.

Идеальный или самый эффективный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло. И это для передовых инженеров уже аксиома или «новая аэродинамика», а Природа это знала ещё со времён первых летающих насекомых и птеродактилей. Так вот, асимметричное атмосферное давление на совершенно плоское крыло возникает и при его нулевом угле наклона к вектору движения набегающего атмосферного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая. В воде «эффект хаоса над крылом» проявляется ещё значительно сильнее.

Это утверждение доказано самой эволюцией живой природы и передовой практикой авиастроения. Смотрим на расправленное крыло любой птицы: сверху оно бархатистое и может играть всеми цветами радуги, что физику говорит о дисперсии света на мельчайших неровностях на поверхности, а снизу – всегда очень плотное, гладкое и со стальным отливом. Смотрим на современный пассажирский «Боинг»: сверху он словно матовый, а снизу – зеркально гладкий. И пусть та положительная разница в атмосферном давлении на крыло, которая возникает только по причине различного качества покрытия его аэродинамических поверхностей, будет и недостаточной для полёта, но именно она и позволит самолёту или птице лететь горизонтально с меньшим углом атаки, то есть с меньшим лобовым сопротивлением, экономя топливо и силы.

Инженеры «Боинга» говорят, что уже экономят на «эффекте хаоса над крылом» до 7-ми процентов топлива, а это огромные деньги. Смотрите фотографии «Боингов» и читайте по запросу «Аэродинамика Боинг». А наши дурни из Сколково одной краской покрывают весь Боинг. Смотрите по запросу «Красим Боинг». Кожа акулы тоже только кажется гладкой, а на ощупь она сравнима с наждачной бумагой. Шершавая кожа способствует образованию хаоса в пограничном слое воды, что ещё больше уменьшает её давление на быструю акулу. И таких примеров «мильён».

Однако вторым законом потоков объясняются не только опыты к теме «Закон Бернулли», но ещё один раз доказывается нечто совсем другое, позволяющее увидеть истоки математического идеализма в физике и похоронить математическую физику, как науку о природе. «Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру» (А. Эйнштейн). Сейчас мы эту словесную формулу математического идеализма просто-напросто докажем. Вернее, я докажу, а вы. согласитесь.

«Все жидкости и газы на Земле имеют вес и находятся под давлением веса собственных и выше расположенных слоёв» (Архимед). Поэтому все прозрачные жидкости и газы состоят из примерно одинаковых, равноудалённых и условно неподвижных (колеблющихся или дрожащих) частиц, находящихся в состоянии взаимного отталкивания и относительного (или чуткого) равновесия и взаимно отталкивающихся в газах на расстояниях много больших, чем в жидкостях. Отсюда: давление в любой точке водоёма или атмосферы равно напряжению взаимного отталкивания равноудалённых частиц в этой точке, и по силе оно равно весу всех частиц над этой точкой. Уберите атмосферное давление, и капля воды тут же исчезнет, разлетевшись на молекулы, а аквариум с водой словно взорвётся. И повинно в том будет как раз-таки «напряжение взаимного отталкивания равноудалённых частиц». Смотрите по запросу «Современный Архимед. Трактат «О плавающих телах» и «К физике антигравитонов». Там есть опыты, позволяющие буквально увидеть неподвижность колеблющихся частиц в жидкостях и в газах. Особенно показателен опыт по мгновенному замерзании переохлаждённой воды при её встряхивании в пластиковой бутылке. Многие его знают, но не понимают.

Способность атомов и молекул к движению взаимного отталкивания пропорциональна температуре. А температура – это «опосредованное мерило» интенсивности атомных и внутриатомных движений и величины гравитационных моментов (квантов, импульсов) атомов, передающихся от атома к атому путём индукции.

И ещё. Всем теоретикам и преподавателям на засыпку: «Какой теорией руководствовались братья Райт, когда делали свой воздушный винт, который у них получился с КПД 78-80%, если научной аэродинамики ещё не было, а КПД самых современных пропеллеров из дерева не превышает 85%?».

Хотелось бы услышать возражения или замечания, но их почему-то нет. Видимо, с тем, что мы живём в эпоху математических лженаук, уже никто не спорит.

Воображеньем прозорливым
К догадкам верным нас несло…
Но сонм учёных кропотливых
Свернул наш поиск — на число.

И лязгом счёта оглушённый
Забыл наш ум — решенья ключ…
Стал слепнуть, в шоры цифр втеснённый.
А был так зряч и так могуч!

Уж цифре памятник построен,
Распята Истина на нём.
Поклонник счёта, жрец и воин
Простёрся ниц перед числом:

Не осознать бедняге в заблужденье,
Как много лжи за ширмой исчисленья!

Источник

Аэродинамические характеристики крыла самолета

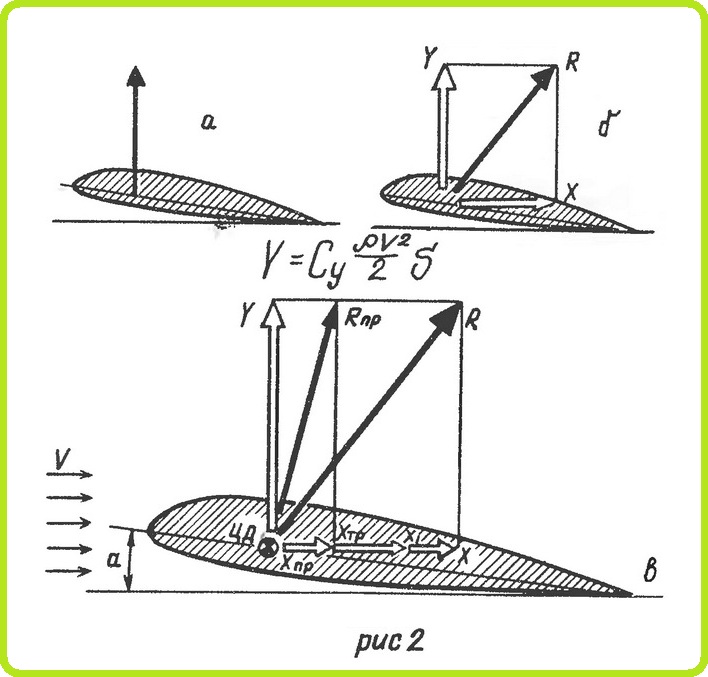
ВСЯКАЯ несущая поверхность, помимо сопротивления, создает еще подъемную силу, обеспечивающую полет летательного аппарата. Единый поток перед крылом разделяется на два неодинаковых потока (рис. 1,а). В верхнем потоке струйки как бы сжимаются, скорость их увеличивается, в нижнем же потоке, наоборот, струйки расширяются и скорость их уменьшается. По закону Бернулли, чем выше скорость, тем меньше давление в струе. Следовательно, над крылом образуется область, давление в которой ниже, чем под крылом.

В зависимости от скорости распределяется и давление по крылу (рис. 1,б). Каждый вектор давления на диаграммах представляет собой силу, которая действует на единицу площади поверхности крыла. Если все эти силы сложить, то получим полную аэродинамическую силу, воздействующую на крыло. Исключением в этом случае будут силы трения, которые по диаграмме распределения давления определить нельзя, так как они направлены по касательной к профилю.

Проекция полной аэродинамической силы на ось, перпендикулярную направлению потока, называется подъемной силой (рис. 2,а). Полную аэродинамическую силу R можно разложить на подъемную силу Y и силу лобового сопротивления X (рис. 2,б.)

Подъемная сила крыла зависит от его геометрических размеров, положения относительно потока, скорости полета модели, плотности воздуха и несущей способности профиля крыла. Эту зависимость принято записывать в виде формулы:

где Cy — коэффициент подъемной силы крыла, учитывающий несущую способность профиля.

Этот коэффициент зависит от формы профиля и угла атаки α — угла между скоростью набегающего воздушного потока и хордой профиля (рис. 2в). Хорда профиля — это условная прямая линия, применяемая для построения профиля, проходящая, как правило, через носик и хвостовик профиля.

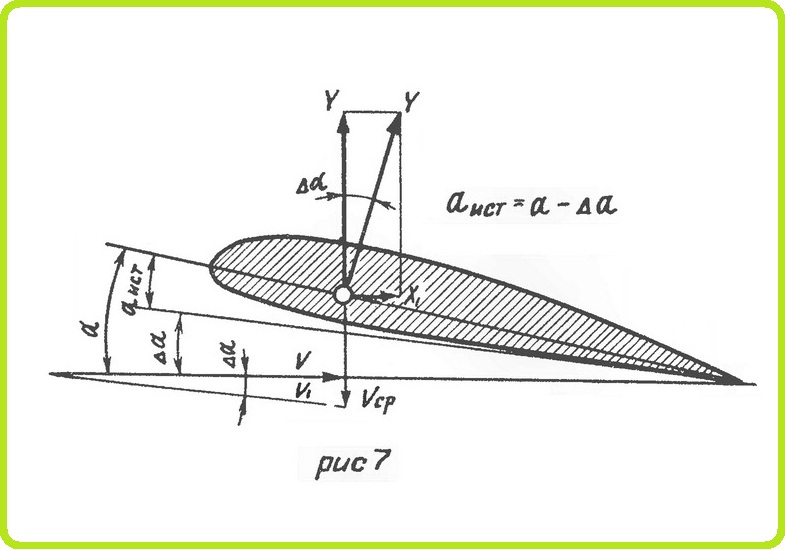
Кроме сопротивления трения и формы, в коэффициент C_x входит еще один третий вид сопротивления — индуктивное. Дело в том, что крыло отбрасывает набегающий на него поток воздуха вниз со скоростью V_cp (рис. 7) так, что в итоге он направлен не по скорости v, a по скорости v₁. Это явление называется скосом потока. Угол отклонения потока ∆α называется углом скоса потока. Сложив геометрически скорости V и V_cp. получают действительное направление и величину скорости потока v1, обтекающего крыло. Изменение направления скорости вызывает, естественно, и изменение угла атаки

Благодаря скосу потока истинный угол атаки меньше геометрического. Угол скоса потока определяется по формуле

где λ — удлинение крыла.

Удлинение крыла λ определяется как отношение квадрата размаха крыла L к площади крыла Sкр

Размах крыла L определяется как расстояние между двумя плоскостями, параллельными плоскости симметрии и касающимися концов крыла.

Подъемная сила всегда направлена перпендикулярно к потоку, обтекающему крыло. Благодаря скосу потока подъемная сила отклонится назад на угол ∆α и будет перпендикулярна новому направлению скорости V₁

Эта подъемная сила называется истинной. Ее можно разложить на две составляющие: перпендикулярную к направлению скорости полета V и параллельную направлению скорости. Эта составляющая, существование которой возможно только при наличии подъемной силы, направлена всегда против движения крыла.

Коэффициент индуктивного сопротивления определяют по формуле

Угол скоса потока и индуктивное сопротивление зависят от формы профиля крыла, удлинения и от угла атаки.

Таким образом, полное лобовое сопротивление крыла конечного размаха состоит из сопротивления формы, сопротивления трения и индуктивного сопротивления (рис. 2в). Соответственно, коэффициент сопротивления крыла выражается формулой

Точка приложения полной аэродинамической силы называется центром давления. Условились считать, что центр давления лежит на хорде крыла. Если характер обтекания правой и левой половины крыла одинаков, центр давления всего крыла лежит в плоскости симметрии. Нарушение геометрической и аэродинамической симметрии крыла вызовет смещение центра давления.

Положение центра давления на хорде зависит от угла атаки и оказывается различным у профилей разной формы. Характер перемещения центра давления вдоль хорды при изменении угла атаки зависит от формы профиля.

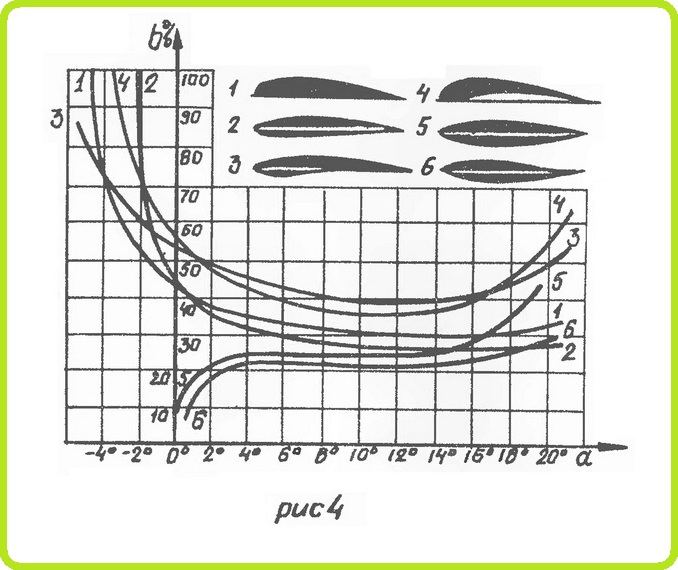
В этом отношении профили делятся на три категории. У несимметричных 1,2 и вогнуто-выпуклых 3,4 профилей (рис. 4), у которых средняя линия вогнута, центр давления при увеличении угла атаки перемещается вперед и наиболее переднее положение занимает при α, близких к α_кр, В этом случае центр давления находится примерно на расстоянии 25—35% хорды от носика профиля. При уменьшении угла атаки он перемещается назад и при углах атаки, на которых Су становится близким к Су = 0, уходит за пределы крыла.

У симметричных профилей 4, имеющих прямую среднюю линию, центр давления в пределах значительного диапазона углов атаки занимает постоянное положение и находится примерно на расстоянии 25% длины хорды от носика. При углах атаки больших критического, центр давления у них резко уходит назад.

У S-образных профилей 6 отогнута вверх задняя кромка. Если хвостик профиля отогнут мало, то перемещение центра давления такое же, как и у профилей первой категории. Бели хвостик отогнут больше, то профиль будет иметь постоянный центр давления. Если же его отогнуть еще больше, то центр давления при увеличении угла атаки отходит назад.

Перемещение центра давления вызывает изменение момента равнодействующей воздушных сил относительно центра тяжести модели. Для того, чтобы судить об устойчивости крыла данного профиля, необходимо знать, как меняется момент воздушных сил, действующих на крыло, с изменением угла атаки.

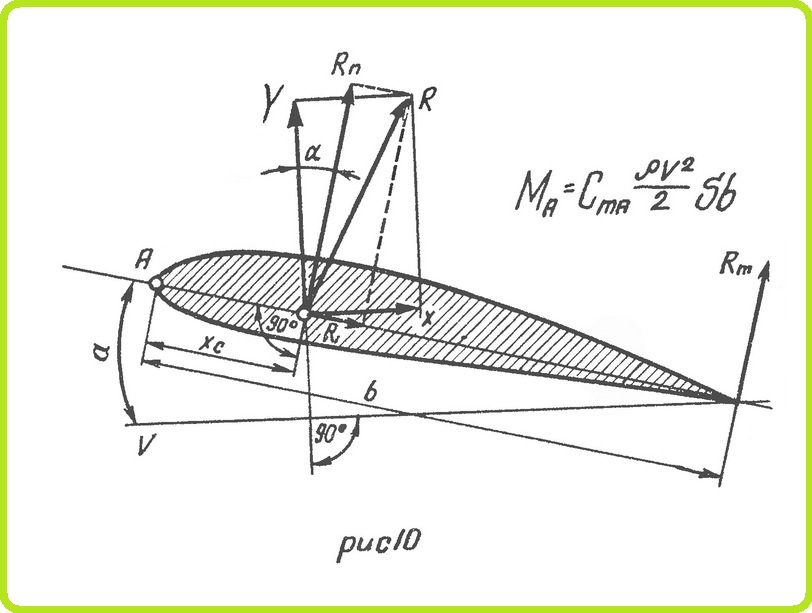
На рис. 10 изображен профиль крыла модели. Так как при предварительных расчетах конструкция модели еще неизвестна, и, следовательно, неизвестно положение ее центра тяжести, вращение крыла рассматривают не относительно центра тяжести, а относительно точки А, находящейся на носике профиля. Силу R раскладывают не на Y и X, как это делалось раньше, а на силы R_n и R_t.

Сила R_n мало отличается от Y, поэтому с небольшой ошибкой можно допустить, что R_n = Y. Момент силы R_n относительно точки А равен

где Х_с— расстояние от центра давления до точки А.

Так как положение центра давления при разных углах атаки неизвестно, то считают, что крыло вращается силой R_m. приложенной на задней кромке профиля. Для этого необходимо, чтобы

Это равенство может сохраняться при разных углах атаки, так как изменение Y и Х_с может соответствовать изменению R_m при постоянном плече b. Величину R_m определяют в аэродинамической трубе из условия равновесия относительно опоры весов. При этом замеряют силу R_m при разных углах атаки. Зная момент, нетрудно подсчитать и коэффициент C_mA в формуле

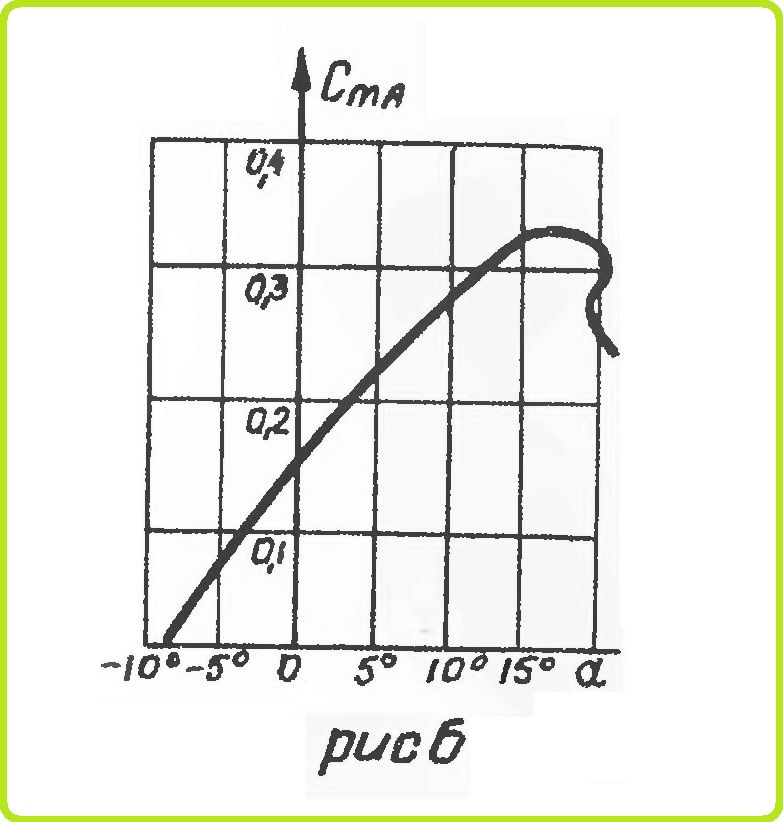
Зависимость коэффициента C_mA от угла атаки α представлена на рис. 6.

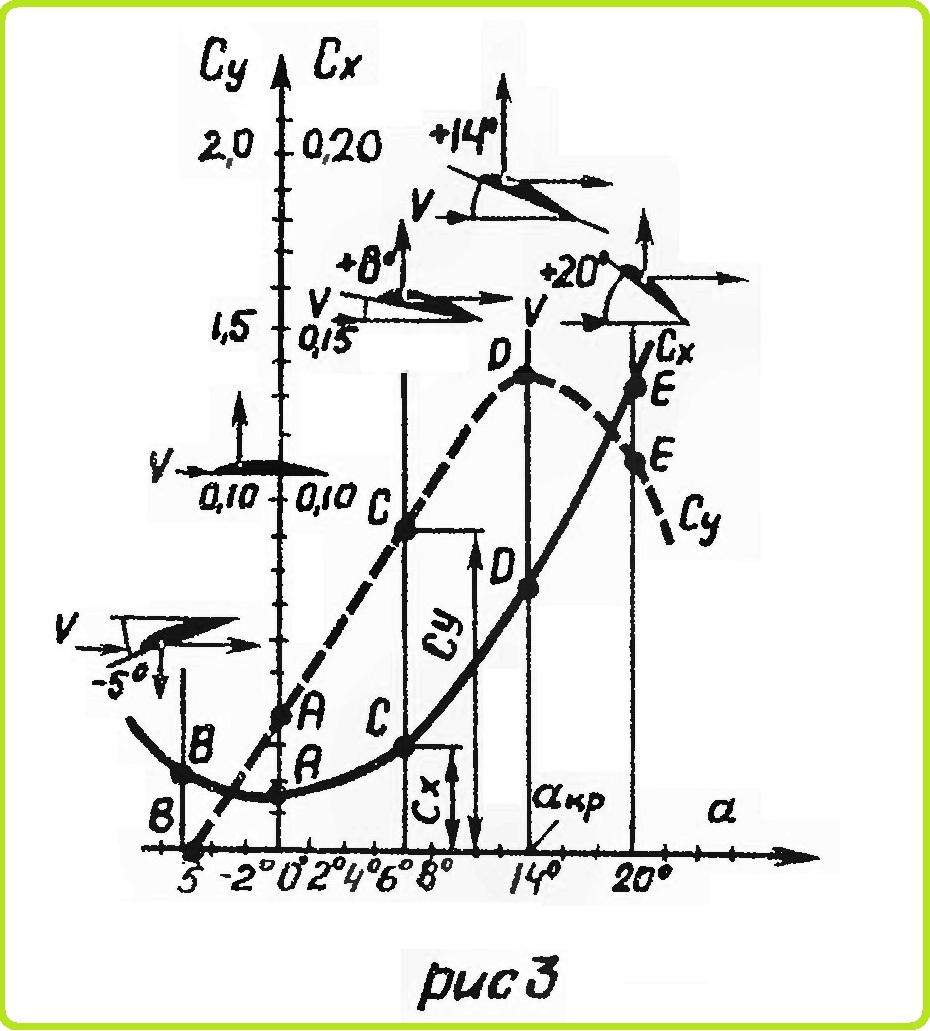
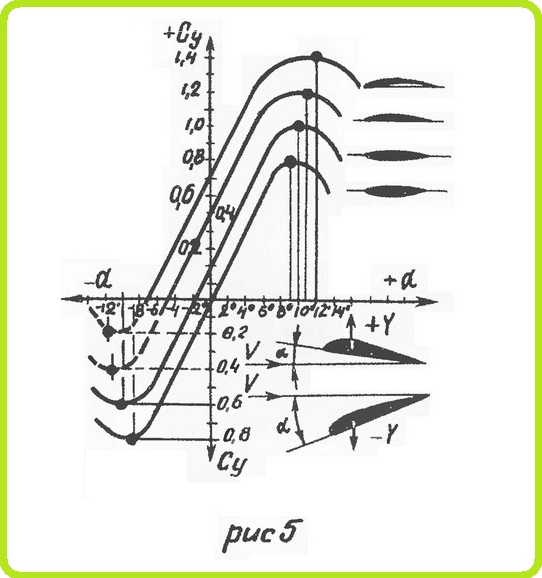
Значение коэффициентов Сх и Су для различных углов атаки — на рис. 3. Значения коэффициентов Су для различных профилей — на рис. 5. Кривая Су по α для симметричного профиля проходит через начало координат. С увеличением вогнутости профиля кривая зависимости Су по α смещается вверх.

Объединенный график зависимости Су от Сх при различных α называется полярой (рис. 8). Имея поляру, можно определить ряд величин, которые характеризуют крыло. Если провести касательную к поляре, параллельную оси Сх, то в точке касания получают угол атаки, соответствующий Су _max (рис. 8). Этот угол называется критическим углом атаки «Крит- При увеличении угла атаки сверх критического нарушается обтекание крыла и подъемная сила уменьшается.

Наивыгоднейшим называется такой угол атаки, при котором отношение коэффициента подъемной силы к коэффициенту лобового сопротивления наибольшее. Чтобы найти этот угол, нужно из начала координат провести касательную к поляре.

Отношение подъемной силы к лобовому сопротивлению называют аэродинамическим качеством крыла.

При полете на угле атаки, имеющем К_max модель проходит наибольшее расстояние. Для того, чтобы модель продержалась наибольшее время в воздухе, необходимо, чтобы угол атаки был равен экономическому углу.

Угол атаки нулевой подъемной силы α₀ лежит на пересечении поляры с осью С_х. При этом угле атаки С_у = 0.

Угол атаки, при котором С_х имеет наименьшее значение С_{х min} находится в точке касания линии к поляре, проведенной параллельно оси С_у.

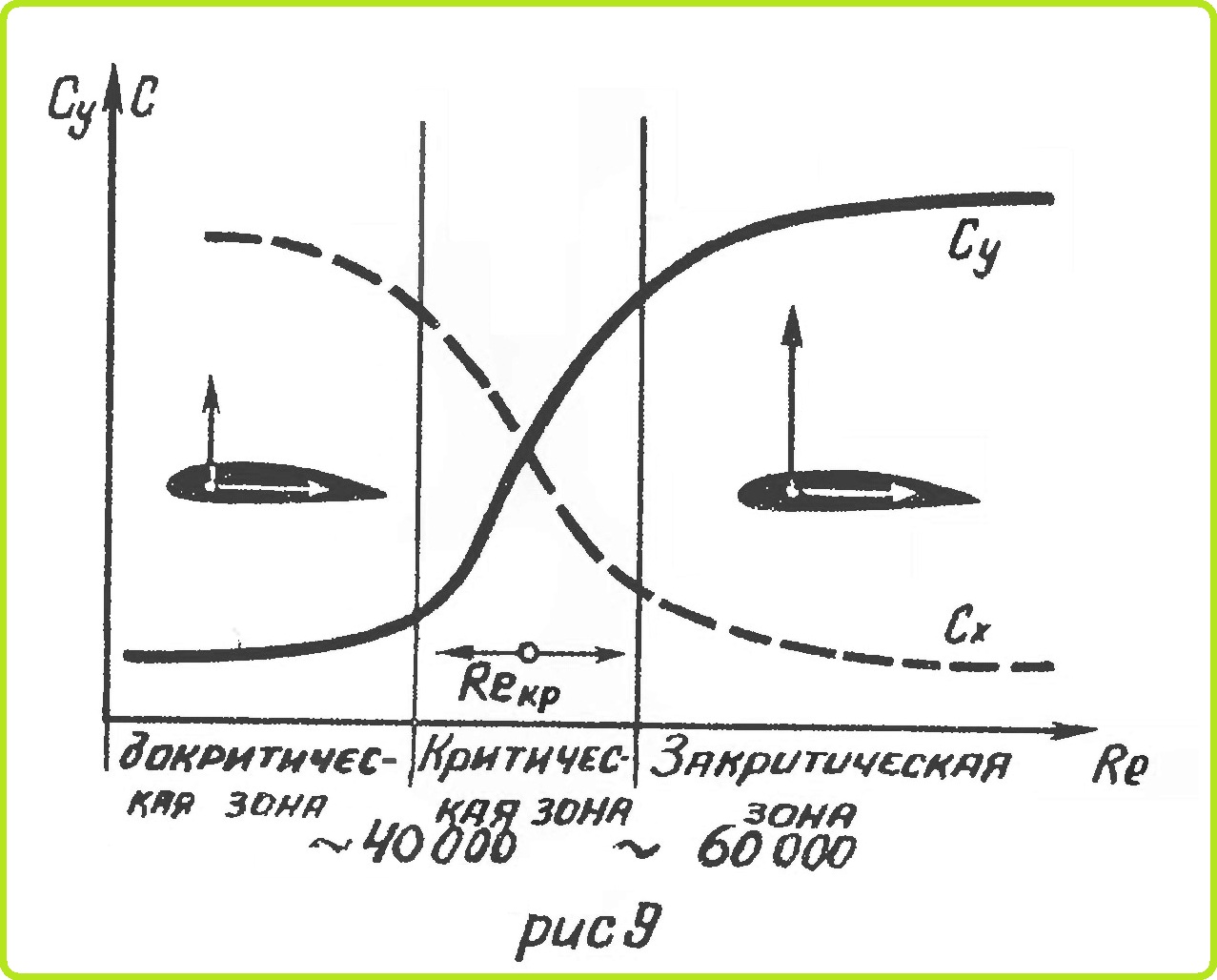
Значения коэффициентов Сх и Су при каком-либо значении угла атаки зависит от числа Re (рис. 9). При Re Re_кpит обтекание профиля потоком турбулентное. Благодаря перемешиванию относительная скорость и кинетическая энергия частиц воздуха вблизи профиля более высокая, чем у ламинарного пограничного слоя, и турбулентный пограничный слой может преодолевать повышенное давление на значительном участке задней поверхности профиля. Точка отрыва турбулентного пограничного слоя лежит вблизи задней кромки и тем ближе к ней, чем меньше перепад давления между соседними точками профиля и чем большую скорость имеет внешний поток. Это приводит к росту Су и уменьшению Сх.

Н. ЛЯШЕНКО, руководитель заводского клуба юных техников Харьков

Источник