Чем меньше угол тем меньше сторона
Чем меньше угол тем меньше сторона
§ 30. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА.
Теорема 1. Против большей стороны в треугольнике лежит и больший угол.
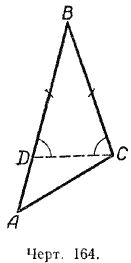
Пусть в /\ АВС сторона АВ больше стороны ВС. Докажем, что угол С, лежащий против большей стороны АВ, больше угла А, лежащего против меньшей стороны ВС (черт. 164).
Треугольник DВС равнобедренный. Угол ВDС равен углу ВСD, так как они лежат против равных сторон в треугольнике.
Угол ВDС — внешний угол треугольника АDС, поэтому он больше угла А.
Так как / ВСD = / ВDС, то и угол ВСD больше угла А: / ВСD > / A. Но угол ВСD составляет только часть всего угла С, поэтому угол С будет и подавно больше угла A.
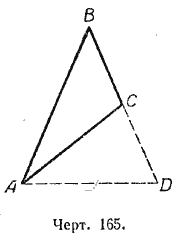
Доказать самостоятельно ту же теорему по чертежу 165, когда ВD = АВ.
В § 18 мы доказали, что в равнобедренном треугольнике углы при основании равны, т. е. в треугольнике против равных сторон лежат равные углы. Докажем теперь обратные теоремы.
Теорема 2. Против равных углов в треугольнике лежат и равные стороны.
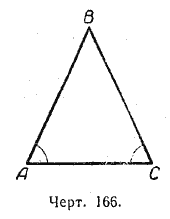
Пусть в /\ AВС / A = / С (черт. 166). Докажем, что AВ = ВС, т. е. треугольник АBС равнобедренный.
Между сторонами АВ и ВС может быть только одно из трёх следующих соотношений:
Докажем, что АВ > АС.
Здесь также может быть одно из трёх следующих соотношений:
Если бы сторона АВ была равна стороне АС, то / С был бы равен / В. Но это противоречит условию теоремы. Значит, АВ не может равняться АС
Точно так же АВ не может быть меньше АС, так как в этом случае угол С был бы меньше угла B, что также противоречит данному условию.
Следовательно, возможен только один случай, а именно:
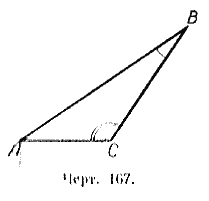
Мы доказали: против большего угла в треугольнике лежит и большая сторона.
Следствие. В прямоугольном треугольнике. гипотенуза больше любого из его катетов.
Чем меньше угол тем меньше сторона
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
 |
Обозначение угла
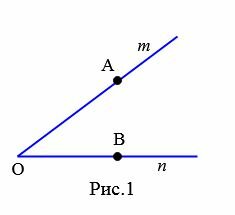
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
Развернутый угол. Внутренняя и внешняя область угла
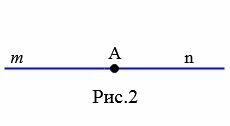
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
 |
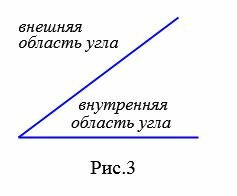
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
 |
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
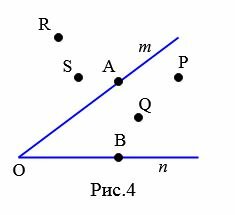
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
 |
Типы углов
В зависимости от величин, углы бывают следующих типов (Рис.5):
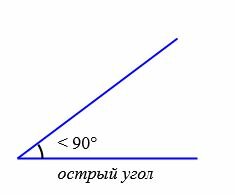 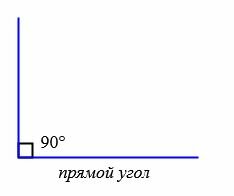 |
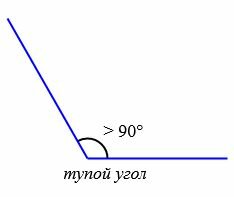  |
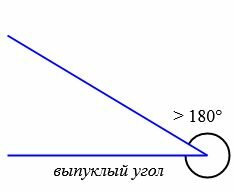 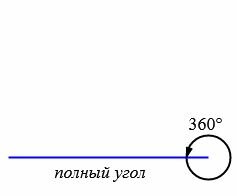 |
Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
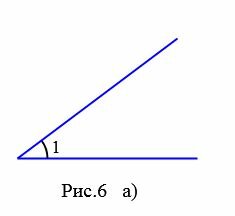 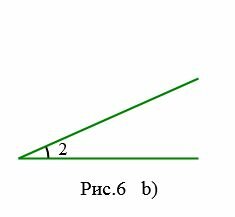 |
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
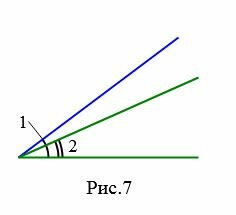 |
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
 |
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Чем меньше угол тем меньше сторона
Экстремальными задачами называют задачи на нахождение наибольших и наименьших значений. Эти задачи имеют большое значение, как для математики, так и для ее приложений.
Здесь мы рассмотрим некоторые классические экстремальные задачи. Часть из них содержится в учебнике: И.М.Смирнова, В.А.Смирнов. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Просвещение, 2002, Мнемозина, 2005.
Начнем с простых задач.
Рассмотрим теперь более трудную задачу.
Развитием задачи Герона является следующая задача.
Если данный угол острый, то угол C ’ OC ” меньше развернутого и, следовательно, прямая C ’ C ” пересекает стороны угла и, значит, задача имеет решение.
Если данный угол прямой, то угол C ’ OC ” – развернутый и, следовательно, прямая C ’ C ” проходит через вершину O угла. В этом случае задача не имеет решения. Какие бы точки A и B на сторонах угла мы не взяли существуют точки A ’, B ’, для которых периметр соответствующего треугольника меньше (рис. 4,в).
Если данный угол тупой, то угол C ’ OC ” – больше развернутого и, следовательно, прямая C ’ C ” не имеет общих точек со сторонами угла. В этом случае задача также не имеет решения. Какие бы точки A и B на сторонах угла мы не взяли, существуют точки A ’, B ’, для которых периметр соответствующего треугольника меньше (рис. 4,г).
Задача 5. Луч света падает на одну сторону угла (рис. 5). Нарисуйте траекторию луча, после отражения его от сторон угла.
Ответ. Искомая траектория показана на рисунке 6. Отраженный от стороны b луч имеет направление противоположное и параллельное направлению падающего луча.
Заметим, что каким бы ни было направление падающего луча света направление отраженного луча всегда будет противоположным и параллельным исходному. Это свойство луча света используется в уголковых отражателях света, которые, в отличие от зеркального отражателя, всегда отражают свет в направлении противоположном исходному (рис. 7).
Задача 6. Может ли бильярдный шар после удара отразиться от двух соседних бортов и пройти через исходную точку: а) в прямоугольном бильярде; б) в треугольном бильярде (рис. 8)?
Задача 7. Нарисуйте траекторию бильярдного шара, при которой, отразившись от трех бортов прямоугольного бильярда, он возвращается в исходную точку.
Решите эту задачу самостоятельно.
Рассмотрим еще одну классическую экстремальную задачу.
Задача 8. В данный остроугольный треугольник вписать треугольник наименьшего периметра.
Задача 9. Найдите путь по поверхности куба ABCDA 1 B 1 C 1 D 1, из вершины A в вершину C 1 наименьшей длины (рис. 10).
Чем меньше угол тем меньше сторона
Экстремальными задачами называют задачи на нахождение наибольших и наименьших значений. Эти задачи имеют большое значение, как для математики, так и для ее приложений.
Здесь мы рассмотрим некоторые классические экстремальные задачи. Часть из них содержится в учебнике: И.М.Смирнова, В.А.Смирнов. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Просвещение, 2002, Мнемозина, 2005.
Начнем с простых задач.
Рассмотрим теперь более трудную задачу.
Развитием задачи Герона является следующая задача.
Если данный угол острый, то угол C ’ OC ” меньше развернутого и, следовательно, прямая C ’ C ” пересекает стороны угла и, значит, задача имеет решение.
Если данный угол прямой, то угол C ’ OC ” – развернутый и, следовательно, прямая C ’ C ” проходит через вершину O угла. В этом случае задача не имеет решения. Какие бы точки A и B на сторонах угла мы не взяли существуют точки A ’, B ’, для которых периметр соответствующего треугольника меньше (рис. 4,в).
Если данный угол тупой, то угол C ’ OC ” – больше развернутого и, следовательно, прямая C ’ C ” не имеет общих точек со сторонами угла. В этом случае задача также не имеет решения. Какие бы точки A и B на сторонах угла мы не взяли, существуют точки A ’, B ’, для которых периметр соответствующего треугольника меньше (рис. 4,г).
Задача 5. Луч света падает на одну сторону угла (рис. 5). Нарисуйте траекторию луча, после отражения его от сторон угла.
Ответ. Искомая траектория показана на рисунке 6. Отраженный от стороны b луч имеет направление противоположное и параллельное направлению падающего луча.
Заметим, что каким бы ни было направление падающего луча света направление отраженного луча всегда будет противоположным и параллельным исходному. Это свойство луча света используется в уголковых отражателях света, которые, в отличие от зеркального отражателя, всегда отражают свет в направлении противоположном исходному (рис. 7).
Задача 6. Может ли бильярдный шар после удара отразиться от двух соседних бортов и пройти через исходную точку: а) в прямоугольном бильярде; б) в треугольном бильярде (рис. 8)?
Задача 7. Нарисуйте траекторию бильярдного шара, при которой, отразившись от трех бортов прямоугольного бильярда, он возвращается в исходную точку.
Решите эту задачу самостоятельно.
Рассмотрим еще одну классическую экстремальную задачу.
Задача 8. В данный остроугольный треугольник вписать треугольник наименьшего периметра.
Задача 9. Найдите путь по поверхности куба ABCDA 1 B 1 C 1 D 1, из вершины A в вершину C 1 наименьшей длины (рис. 10).
Урок математики на тему: «Угол.Какой угол меньше?»
Темы: «Угол»; «Какой угол меньше?»
– введение в рассмотрение геометрических фигур новой фигуры – угол (лучи и внутренняя область);
– формирование понимания того, что две пересекающиеся прямые образуют 4 угла;
– построение двух углов с общей вершиной;
– построение двух углов с общей стороной;
– сравнение углов способом наложения;
– формирование УУД: построение геометрических фигур.
Пропедевтика: прямой, острый, тупой углы.
Повторение : Какие бывают линии: прямая, отрезок, точка, луч. Чем они отличаются?
2. Сообщение темы урока. (слайд 1)
У-1, Т-1, З., К., простой и цветные карандаши, линейка, веер.
Вводная часть уроков
Учащиеся открывают в учебнике «Содержание» (с. 4), находят тему урока, отмечают
записывают в тетрадях дату, озвучивают тему урока.
• Сами читаем диалог между Машей и Мишей, из которого дети узнают, как Маша построила угол.
• Предлагаем детям найти угол, построенный Машей, и отметить его фишкой желтого цвета.
• Читаем последний абзац текста и предлагаем отметить угол, построенный Мишей, фишкой голубого цвета.
Задание No 1 (У-1, с. 63–64)
• Предлагаем учащимся самостоятельно построить угол.
• После окончания работы акцентируем внимание детей на том, что геометрическая фигура, которая называется углом, – это два луча и внутренняя область между ними.
• Чертим угол на классной доске, закрашивая его внутреннюю область цветным мелом. Спрашиваем: а каким цветом выделили угол вы?
• Объясняем детям, что лучи, которые образуют угол, называются
• Задаем вопросы: чем отличаются стороны угла от сторон многоугольника? (Стороны угла – лучи, они бесконечны. Стороны многоугольника – отрезки.) Сколько вершин имеет угол? (Одну вершину.)
Задание No 2 (У-1, с. 64)
• Предлагаем учащимся прочитать и выполнить это задание самостоятельно. Даем время на его выполнение.
• Учащиеся устно отвечают на вопросы, а мы показываем на доске с помощью указки все четыре угла, полученные при пересечении двух прямых.
Сколько углов получилось? Обозначить дугой.
• Обращаем внимание детей на то, что все углы имеют общую вершину, а каждая пара углов – общую вершину и общую сторону.
Задание No 1 (У-1, с. 65)
Объяснение нового материала
• Сами читаем задания, давая учащимся время на обдумывание. Учащиеся рассматривают углы и формулируют ответы, опираясь на цвет углов. Например: угол розового цвета расположен внутри угла голубого цвета.
Как вы думаете какой угол больше? А какой угол меньше?
Читаем правило под рисунком.
• Акцентируем внимание детей на словосочетании «один угол расположен внутри другого» (т. е. у этих углов есть общая вершина и одна общая сторона).
У вас на парте два угла, давайте их сравним. Каким способ мы это сделаем? (наложение одного угла на другой)
• Сами формулируем определение, которое позволит сравнивать углы по величине способом наложения: угол, который расположен внутри другого, называют меньшим углом.
• Просим одного-двух учеников повторить это определение.
Задание No 2 (У-1, с. 65)
• Подсказываем детям, что необходимо сравнить углы розового, желтого и зеленого цветов. Например: угол зеленого цвета находится внутри угла желтого и розового цвета, значит, он меньше и того и другого.
Итог урока : Давайте вспомним: какую цель мы ставили в начале урока? Что такое угол? Как называются лучи при построении угла?
Что такое вершина?( точка из которой выходят лучи) Как сравнить углы? (наложением)