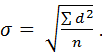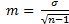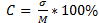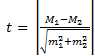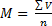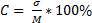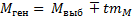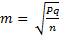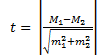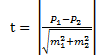Чем меньше вариабельность признака тем величина средней ошибки

V. Вариационные ряды, средние величины, вариабельность признака

Особое место в статистическом анализе принадлежит определению среднего уровня изучаемого признака или явления. Средний уровень признака измеряют средними величинами.

Средняя величина характеризует общий количественный уровень изучаемого признака и является групповым свойством статистической совокупности. Она нивелирует, ослабляет случайные отклонения индивидуальных наблюдений в ту или иную сторону и выдвигает на первый план основное, типичное свойство изучаемого признака.

Средние величины широко используются:

1. Для оценки состояния здоровья населения: характеристики физического развития (рост, вес, окружность грудной клетки и пр.), выявления распространенности и длительности различных заболеваний, анализа демографических показателей (естественного движения населения, средней продолжительности предстоящей жизни, воспроизводства населения, средней численности населения и др.).

2. Для изучения деятельности лечебно-профилактических учреждений, медицинских кадров и оценки качества их работы, планирования и определения потребности населения в различных видах медицинской помощи (среднее число обращений или посещений на одного жителя в год, средняя длительность пребывания больного в стационаре, средняя продолжительность обследования больного, средняя обеспеченность врачами, койками и пр.).

3. Для характеристики санитарно-эпидемиологического состояния (средняя запыленность воздуха в цехе, средняя площадь на одного человека, средние нормы потребления белков, жиров и углеводов и т. д.).

4. Для определения медико-физиологических показателей в норме и патологии, при обработке лабораторных данных, для установления достоверности результатов выборочного исследования в социально-гигиенических, клинических, экспериментальных исследованиях.

Вычисление средних величин выполняется на основе вариационных рядов. Вариационный ряд – это однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления.

Количественная вариация может быть двух типов: прерывная (дискретная) и непрерывная.

Прерывный (дискретный) признак выражается только целым числом и не может иметь никаких промежуточных значений (например, число посещений, численность населения участка, число детей в семье, степень тяжести болезни в баллах и др.).

Непрерывный признак может принимать любые значения в определенных пределах, в том числе и дробные, и выражается лишь приближенно (например, вес – для взрослых можно ограничиться килограммами, а для новорожденных – граммами; рост, артериальное давление, время, потраченное на прием больного, и т. д.).

Цифровое значение каждого отдельного признака или явления, входящего в вариационный ряд, называется вариантой и обозначается буквой V. В математической литературе встречаются и другие обозначения, например x или y.

Вариационный ряд, где каждая варианта указана один раз, называется простым. Такие ряды используются в большинстве статистических задач в случае компьютерной обработки данных.

При увеличении числа наблюдений, как правило, встречаются повторяющиеся значения вариант. В этом случае создается сгруппированный вариационный ряд, где указывается число повторений (частота, обозначается буквой «р»).

Ранжированный вариационный ряд состоит из вариант, расположенных в порядке возрастания или убывания. Как простой, так и сгруппированный ряды могут быть составлены с ранжированием.

Интервальный вариационный ряд составляют с целью упрощения последующих вычислений, выполняемых без использования компьютера, при очень большом числе единиц наблюдения (более 1000).

Непрерывный вариационный ряд включает значения вариант, которые могут выражаться любыми значениями.

Если в вариационном ряде значения признака (варианты) заданы в виде отдельных конкретных чисел, то такой ряд называют дискретным.

Общими характеристиками значений признака, отражаемого в вариационном ряду, являются средние величины. Среди них наиболее применяемые: средняя арифметическая величина М, мода Мо и медиана Me. Каждая из этих характеристик своеобразна. Они не могут подменить друг друга и лишь в совокупности достаточно полно и в сжатой форме представляют собой особенности вариационного ряда.

Модой (Мо)называют значение наиболее часто встречающейся варианты.

Медиана (Me) – это значение варианты, делящей ранжированный вариационный ряд пополам (с каждой стороны медианы находится половина вариант). В редких случаях, когда имеется симметричный вариационный ряд, мода и медиана равны между собой и совпадают со значением средней арифметической.

Наиболее типичной характеристикой значений вариант является средняя арифметическая величина(М). В математической литературе она обозначается .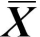

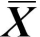
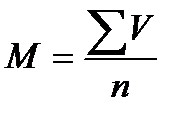
Средняя арифметическая величина (M, ) – это общая количественная характеристика определенного признака изучаемых явлений, составляющих качественно однородную статистическую совокупность. Различают среднюю арифметическую простую и взвешенную. Средняя арифметическая простая вычисляется для простого вариационного ряда путем суммирования всех вариант и делением этой суммы на общее количество вариант, входящих в данный вариационный ряд. Вычисления проводятся по формуле:

,

ΣV— сумма вариант;

В сгруппированном вариационном ряду определяют взвешенную среднюю арифметическую. Формула ее вычисления:

,

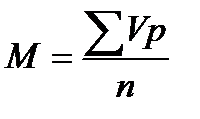
где: М— средняя арифметическая взвешенная;

При большом числе наблюдений в случае ручных вычислений может применяться способ моментов.

Средняя арифметическая имеет следующие свойства:

· сумма отклонений вариант от средней (Σd) равна нулю (см. табл. 15);

· при умножении (делении) всех вариант на один и тот же множитель (делитель) средняя арифметическая умножается (делится) на тот же множитель (делитель);

· если прибавить (вычесть) ко всем вариантам одно и то же число, средняя арифметическая увеличивается (уменьшается) на это же число.

Средние арифметические величины, взятые сами по себе, без учета вариабельности рядов, из которых они вычислены, могут не в полной мере отражать свойства вариационного ряда, в особенности когда необходимо сопоставление с другими средними. Близкие по значению средние могут быть получены из рядов с различной степенью рассеяния. Чем ближе друг к другу отдельные варианты по своей количественной характеристике, тем меньше рассеяние (колеблемость, вариабельность) ряда, тем типичнее его средняя.

Основными параметрами, которые позволяют оценить вариабельность признака, являются:

· Среднее квадратическое отклонение;

Поскольку отклонения вариант от средней могут быть положительными и отрицательными, то при суммировании они дают значение «0» (Sd=0). Чтобы избежать этого, величины отклонения (d) возводятся во вторую степень и усредняются. Таким образом, дисперсия вариационного ряда является средним квадратом отклонений вариант от средней арифметической и вычисляется по формуле:

.

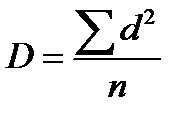
Она является важнейшей характеристикой вариабельности и применяется для вычисления многих статистических критериев.

Поскольку дисперсия выражается квадратом отклонений, ее величина не может использоваться в сопоставлении со средней арифметической. Для этих целей применяется среднее квадратическое отклонение, которое обозначается знаком «Сигма» (σ). Оно характеризует среднее отклонение всех вариант вариационного ряда от средней арифметической величины в тех же единицах, что и сама средняя величина, поэтому они могут использоваться совместно.

Среднее квадратическое отклонение определяют по формуле:

.

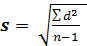
стандартное отклонение (s) – это оценка среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии.

При значениях n > 30 среднее квадратическое отклонение (σ) и стандартное отклонение (s) будут одинаковыми (σ =s). Поэтому в большинстве практических пособий эти критерии рассматриваются как разнозначные. В программе Excel вычисление стандартного отклонения может быть выполнено функцией =СТАНДОТКЛОН(диапазон). А с целью расчета среднего квадратического отклонения требуется создать соответствующую формулу.

Среднее квадратическое или стандартное отклонение позволяет определить, насколько значения признака могут отличаться от среднего значения. Предположим, существуют два города с одинаковой средней дневной температурой в летний период. Один их этих городов расположен на побережье, а другой на континенте. Известно, что в городах, расположенных на побережье, различия дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднее квадратическое отклонение дневных температур у прибрежного города будет меньше, чем у второго города. На практике это означает, что средняя температура воздуха каждого конкретного дня в городе, расположенного на континенте будет сильнее отличаться от среднего значения, чем в городе на побережье. Кроме того стандартное отклонение позволяет оценить возможные отклонения температуры от средней с требуемым уровнем вероятности.

Величина среднего квадратического отклонения позволяет судить о характере однородности вариационного ряда и исследуемой группы. Если величина среднего квадратического отклонения небольшая, то это свидетельствует о достаточно высокой однородности изучаемого явления. Среднюю арифметическую в таком случае следует признать вполне характерной для данного вариационного ряда. Однако слишком малая величина сигмы заставляет думать об искусственном подборе наблюдений. При очень большой сигме средняя арифметическая в меньшей степени характеризует вариационный ряд, что говорит о значительной вариабельности изучаемого признака или явления или о неоднородности исследуемой группы. Однако сопоставление величины среднего квадратического отклонения возможно только для признаков одинаковой размерности. Действительно, если сравнивать разнообразие веса новорожденных детей и взрослых, мы всегда получим более высокие значения сигмы у взрослых.

Сравнение вариабельности признаков различной размерности может быть выполнено с помощью коэффициента вариации. Он выражает разнообразие в процентах от средней величины, что позволяет производить сравнение различных признаков. Коэффициент вариации в медицинской литературе обозначается знаком «С», а в математической «v» и вычисляемого по формуле:

.

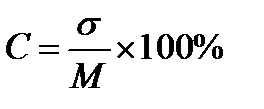
Значения коэффициента вариации менее 10% свидетельствует о малом рассеянии, от 10 до 20% – о среднем, более 20% – о сильном рассеянии вариант вокруг средней арифметической.

Средняя арифметическая величина, как правило, вычисляется на основе данных выборочной совокупности. При повторных исследованиях под влиянием случайных явлений средняя арифметическая может изменяться. Это обусловлено тем, что исследуется, как правило, только часть возможных единиц наблюдения, то есть выборочная совокупность. Информация обо всех возможных единицах, представляющих изучаемое явление, может быть получена при изучении всей генеральной совокупности, что не всегда возможно. В то же время с целью обобщения данных эксперимента представляет интерес величина средней в генеральной совокупности. Поэтому для формулировки общего вывода об изучаемом явлении, результаты, полученные на основе выборочной совокупности, должны быть, перенесены на генеральную совокупность статистическими методами.

Чтобы определить степень совпадения выборочного исследования и генеральной совокупности, необходимо оценить величину ошибки, которая неизбежно возникает при выборочном наблюдении. Такая ошибка называется «Ошибкой репрезентативности» или «Средней ошибкой средней арифметической». Она фактически является разностью между средними, полученными при выборочном статистическом наблюдении, и аналогичными величинами, которые были бы получены при сплошном исследовании того же объекта, т.е. при изучении генеральной совокупности. Поскольку выборочная средняя является случайной величиной, такой прогноз выполняется с приемлемым для исследователя уровнем вероятности. В медицинских исследованиях он составляет не менее 95%.

Ошибку репрезентативности нельзя смешивать с ошибками регистрации или ошибками внимания (описки, просчеты, опечатки и др.), которые должны быть сведены до минимума адекватной методикой и инструментами, применяемыми при проведении эксперимента.

Величина ошибки репрезентативности зависит как от объема выборки, так и от вариабельности признака. Чем больше число наблюдений, тем ближе выборка к генеральной совокупности и тем меньше ошибка. Чем более изменчив признак, тем больше величина статистической ошибки.

На практике для определения ошибки репрезентативности в вариационных рядах пользуются следующей формулой:

,

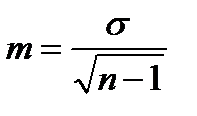
где: m – ошибка репрезентативности;

σ – среднее квадратическое отклонение;

n – число наблюдений в выборке.

Из формулы видно, что размер средней ошибки прямо пропорционален среднему квадратическому отклонению, т. е. вариабельности изучаемого признака, и обратно пропорционален корню квадратному из числа наблюдений.

При выполнении статистического анализа на основе вычисления относительных величин построение вариационного ряда не является обязательным. При этом определение средней ошибки для относительных показателей может выполняться по упрощенной формуле:

,

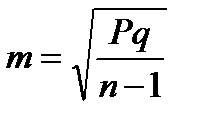
где: Р – величина относительного показателя, выраженного в процентах, промилле и т.д.;

q – величина, обратная Р и выраженная как (1-Р), (100-Р), (1000-Р) и т. д., в зависимости от основания, на которое рассчитан показатель;

n – число наблюдений в выборочной совокупности.

Однако, указанная формула вычисления ошибки репрезентативности для относительных величин может применяться только в том случае, когда значение показателя меньше его основания. В ряде случаев расчета интенсивных показателей такое условие не соблюдается, и показатель может выражаться числом более 100% или 1000%о. В такой ситуации выполняется построение вариационного ряда и вычисление ошибки репрезентативности по формуле для средних величин на основе среднего квадратического отклонения.

Прогнозирование величины средней арифметической в генеральной совокупности выполняется с указанием двух значений – минимального и максимального. Эти крайние значения возможных отклонений, в пределах которых может колебаться искомая средняя величина генеральной совокупности, называются «Доверительные границы».

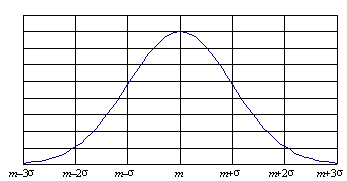
Постулатами теории вероятностей доказано, что при нормальном распределении признака с вероятностью 99,7%, крайние значения отклонений средней будут не больше величины утроенной ошибки репрезентативности (М ± 3m); в 95,5% – не больше величины удвоенной средней ошибки средней величины (М ± 2m ); в 68,3% – не больше величины одной средней ошибки (М± 1m) (рис. 9).

Рис. 9. Плотность вероятностей нормального распределения.

Отметим, что приведенное выше утверждение справедливо только для признака, который подчиняется нормальному закону распределения Гаусса.

Большинство экспериментальных исследований, в том числе и в области медицины, связано с измерениями, результаты которых могут принимать практически любые значения в заданном интервале, поэтому, как правило, описываются моделью непрерывных случайных величин. В связи с этим в большинстве статистических методов рассматриваются непрерывные распределения. Одним из таких распределений, имеющим основополагающую роль в математической статистике, является нормальное, или гауссово, распределение.

Это объясняется целым рядом причин.

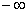
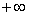
1. Прежде всего, многие экспериментальные наблюдения можно успешно описать с помощью нормального распределения. Следует сразу же отметить, что не существует распределений эмпирических данных, которые были бы в точности нормальными, поскольку нормально распределенная случайная величина находится в пределах от до , чего никогда не встречается на практике. Однако нормальное распределение очень часто хорошо подходит как приближение.

2. Многие распределения, связанные со случайной выборкой, при увеличении объема последней переходят в нормальное.

3. Нормальное распределение хорошо подходит в качестве приближенного описания других непрерывных распределений (например, асимметричных).[a13]

4. Нормальное распределение обладает рядом благоприятных математических свойств, во многом обеспечивших его широкое применение в статистике.

В то же время следует отметить, что в медицинских данных встречается много экспериментальных распределений, описание которых моделью нормального распределения невозможно. Для этого в статистке разработаны методы, которые принято называть «Непараметрическими».

Выбор статистического метода, который подходит для обработки данных конкретного эксперимента, должен производиться в зависимости от принадлежности полученных данных к нормальному закону распределения. Проверка гипотезы на подчинение признака нормальному закону распределения выполняется с помощью гистограммы распределения частот (графика), а также ряда статистических критериев. Среди них:

— Критерий асимметрии (b);

— Критерий проверки на эксцесс (g);

Анализ характера распределения данных (его еще называют проверкой на нормальность распределения) осуществляется по каждому параметру. Чтобы уверенно судить о соответствии распределения параметра нормальному закону, необходимо достаточно большое число единиц наблюдения (не менее 30 значений).

Для нормального распределения критерии асимметрии и эксцесса принимают значение 0. Если распределение смещено вправо b > 0 (положительная асимметрия), при b 0 кривая распределения острее, если g

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

УТОЧНЕНИЕ ПРИЧИН СМЕРТИ ПО ДАННЫМ ПАТОЛОГОАНАТОМИЧЕСКИХ ВСКРЫТИЙ 2 страница

6.104. Формула вычисления коэффициента вариации …

1)

2)

3)

Решение:формула вычисления коэффициента вариации: .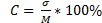

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

6.105. Степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации до 10%, является …

Решение:степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации до 10%, является малой.

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

6.106. Степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации от 10 до 20%, является …

Решение:степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации от 10 до 20%, является средней.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

6.107. Степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации более 20%, является …

Решение:степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации более 20%, является сильной.

Правильный ответ: 3.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

Тема 6.6. Репрезентативность выборочной совокупности, правило трех сигм (Л.Н. Грибина, А.Н. Голубев)

1) правило отбора единиц наблюдения в статистическую совокупность

2) вероятностная зависимость между значением средней арифметической, средним квадратическим отклонением и вариантами

3) отношение средней величины к среднему квадратическому отклонению

Правильный ответ: 2.

Литература: Общественное здоровье и здравоохранение, экономика здравоохранения: учебник: в 2 т. / под ред. В. З. Кучеренко – М.: ГЕОТАР-Медиа, 2013, стр. 79-81.

6.109. интервал трех сигм – это …

1) размах колебаний вариант в вариационном ряду, который можно оценить статистическими методами

2) разница между максимальной и минимальной вариантами

3) разница между средним квадратическим отклонением и ошибкой репрезентативности

4) отношение средней величины к среднему квадратическому отклонению выраженное в %

Решение:интервал трех сигм – это размах колебаний вариант в вариационном ряду, который можно оценить статистическими методами.

Правильный ответ: 1.

Литература: Общественное здоровье и здравоохранение, экономика здравоохранения: учебник: в 2 т. / под ред. В. З. Кучеренко – М.: ГЕОТАР-Медиа, 2013, стр. 79-81.

6.110. СВОЙСТВО РЕПРЕЗЕНТАТИВНОСТИ ХАРАКТЕРНО ДЛЯ СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ …

Решение:свойство репрезентативности характерно для выборочной статистической совокупности.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

6.111. РЕПРЕЗЕНТАТИВНОСТЬ – ЭТО …

1) соответствие средней арифметической величины выборочной совокупности аналогичному параметру генеральной совокупности

2) понятие, характеризующее связь между признаками

3) характеристика методики исследования

Решение:репрезентативность – это соответствие средней арифметической величины выборочной совокупности аналогичному параметру генеральной совокупности.

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 75.

6.112. С УВЕЛИЧЕНИЕМ ОБЪЕМА НАБЛЮДЕНИЙ ОШИБКА РЕПРЕЗЕНТАТИВНОСТИ …

2) остается без изменений

Решение:с увеличением объема наблюдений ошибка репрезентативности уменьшается.

Правильный ответ: 3.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 76.

6.113. Ошибка репрезентативности:

1) является мерой изменчивости значения средней арифметической, которая может быть получена при повторных исследованиях

2) позволяет с определенной вероятностью перенести результаты изучения признака в выборочной совокупности на генеральную совокупность

3) служит оценкой рассеяния вариант

Решение:ошибка репрезентативности: является мерой изменчивости значения средней арифметической, которая может быть получена при повторных исследованиях и позволяет с определенной вероятностью перенести результаты изучения признака в выборочной совокупности на генеральную совокупность.

Правильный ответ: 1, 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.114. Степень совпадения выборочной совокупности с генеральной оценивается с помощью …

1) коэффициента корреляции

2) среднего квадратического отклонения

3) ошибки репрезентативности

Решение:степень совпадения выборочной совокупности с генеральной оценивается с помощью ошибки репрезентативности.

Правильный ответ: 3.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.115. Репрезентативность выборочной совокупности обеспечивается:

1) соответствующим числом единиц наблюдения

3) случайностью отбора единиц наблюдения

4) кодированием единиц наблюдения

Решение:репрезентативность выборочной совокупности обеспечивается соответствующим числом единиц наблюдения, а также случайностью отбора единиц наблюдения.

Правильный ответ: 1, 3.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 76.

6.116. ФОРМУЛА ВЫЧИСЛЕНИЯ СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ …

1)

2)

3)

4)

Решение:формула вычисления среднего квадратического отклонения: .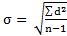

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 69.

6.117. ФОРМУЛА ВЫЧИСЛЕНИЯ ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ В ВАРИАЦИОННОМ РЯДУ …

1)

2)

3)

4)

Решение:формула вычисления ошибки репрезентативности в вариационном ряду: .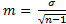

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 76.

6.118. ФОРМУЛА ВЫЧИСЛЕНИЯ ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ ДЛЯ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН …

1)

2)

3)

4)

Решение:формула вычисления ошибки репрезентативности для относительных величин: .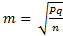

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 75.

6.119. Величина ошибки репрезентативности зависит от:

1) числа наблюдений

2) среднего квадратического отклонения

3) коэффициента корреляции

4) критерия Стьюдента

Решение:величина ошибки репрезентативности зависит от среднего квадратического отклонения и числа наблюдений.

Правильный ответ: 1, 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 76.

6.120. При проведении медико-социальных исследований в выборочной совокупности невозможно избежать …

1) арифметических ошибок вычислений

2) ошибок степени точности вычисления (округления чисел)

3) методических ошибок организации исследования

4) ошибок репрезентативности

Решение:при проведении медико-социальных исследований в выборочной совокупности невозможно избежать ошибок репрезентативности.

Правильный ответ: 4.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

6.121. ЧТОБЫ УМЕНЬШИТЬ ОШИБКУ РЕПРЕЗЕНТАТИВНОСТИ, ЧИСЛО НАБЛЮДЕНИЙ НЕОБХОДИМО …

3) оставить без изменения

Решение:чтобы уменьшить ошибку репрезентативности, число наблюдений необходимо увеличить.

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 74.

6.122. ЧЕМ МЕНЬШЕ ЧИСЛО НАБЛЮДЕНИЙ, ТЕМ ВЕЛИЧИНА ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ …

Решение:чем меньше число наблюдений, тем величина ошибки репрезентативности больше.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 76.

6.123. ЧЕМ МЕНЬШЕ ВАРИАБЕЛЬНОСТЬ ПРИЗНАКА, ТЕМ ВЕЛИЧИНА СРЕДНЕЙ ОШИБКИ …

Решение:чем меньше вариабельность признака, тем величина средней ошибки меньше.

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 76.

Тема 6.7. Доверительные границы колебаний средней величины (Л.Н. Грибина, А.Н. Голубев)

1) вероятностная оценка возможных отклонений, в пределах которых может колебаться искомая средняя величина признака при повторных исследованиях

2) разница между максимальной и минимальной вариантами

3) разница между средним квадратическим отклонением и ошибкой репрезентативности

4) отношение средней величины к среднему квадратическому отклонению

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.125. Доверительные границы относительной величины определяют по формуле…

1)

2)

3)

4)

Решение:доверительные границы относительной величины определяют по формуле .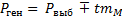

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.126. Доверительные границы средней величины определяют по формуле…

1)

2)

3)

4)

Решение:доверительные границы относительной величины определяют по формуле .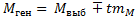

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.127. При числе наблюдений n более 30 и доверительной вероятности p=95,5% величина доверительного коэффициента (t) принимается равной …

4) табличному значению для степени свободы k = n-1

Решение:при числе наблюдений n более 30 и доверительной вероятности p=95,5% величина доверительного коэффициента (t) принимается равной 2.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.128. При числе наблюдений n менее 30 и доверительной вероятности p=95,5% величина доверительного коэффициента (t) принимается равной …

4) табличному значению для степени свободы k = n-1

Решение:при числе наблюдений n менее 30 и доверительной вероятности p=95,5% величина доверительного коэффициента (t) принимается равной табличному значению для степени свободы k = n-1.

Правильный ответ: 4.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.129. При числе наблюдений n более 30 и доверительной вероятности p=99,7% величина доверительного коэффициента (t) принимается равной …

4) табличному значению для степени свободы k = n-1

Решение:при числе наблюдений n более 30 и доверительной вероятности p=99,7% величина доверительного коэффициента (t) принимается равной 3.

Правильный ответ: 3.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.130. Доверительные границы средней арифметической с вероятностью, достаточной для медико-биологических исследований При числе наблюдений n более 30, вычисляются по формуле…

1) М ± 1m, вероятность 68,3%

2) М ± 2m, вероятность 95,5%

3) М ± 3m, вероятность 99,9%

Решение:доверительные границы средней арифметической с вероятностью 95,5%, достаточной для медико-биологических исследований, вычисляются по формуле М ± 2m.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.131. ВЕРОЯТНОСТЬ БЕЗОШИБОЧНОГО ПРОГНОЗА, достаточная для оценки данных МЕДИКО-БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ, составляет …

Решение:вероятность безошибочного прогноза для медико-биологических исследований, составляет 95,5%.

Правильный ответ: 4.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

6.132. ЕСЛИ ИЗВЕСТНО, ЧТО М = 40,0кг, σ=3,0кг, ТО КРАЙНИЕ ВАРИАНТЫ ВАРИАЦИОННОГО РЯДА, С ВЕРОЯТНОСТЬЮ ПРОГНОЗА 99,7%, БУДУТ НАХОДИТЬСЯ В ДИАПАЗОНЕ …

Решение:рассеяние вариант вокруг средней арифметической с вероятностью 99,7% определяется в интервале М ± 3σ, если известно, что м=40,0кг, а σ=3,0кг, то крайние варианты вариационного ряда, с вероятностью прогноза 99,7%, будут находиться в диапазоне от 31 до 49кг.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77-82.

6.133. ГРАНИЦЫ ВОЗМОЖНЫХ СЛУЧАЙНЫХ КОЛЕБАНИЙ СРЕДНЕЙ ВЕЛИЧИНЫ В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ С ВЕРОЯТНОСТЬЮ ПРОГНОЗА 95,5 % лежат В ПРЕДЕЛАХ …

Решение:границы возможных случайных колебаний средней величины в генеральной совокупности с вероятностью прогноза 95,5 % лежат в пределах M ± 2m.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77-82.

6.134. ДОВЕРИТЕЛЬНЫЫЕ ГРАНИЦЫ М±3m СООТВЕТСТВУЮТ ВЕРОЯТНОСТИ ПРОГНОЗА …

Решение:доверительные границы м±3m соответствуют вероятности прогноза 99,7%.

Правильный ответ: 3.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77.

Тема 6.8. Проверка статистических гипотез, достоверность различий вариационных рядов (Л.Н. Грибина, А.Н. Голубев)

6.135. ДЛЯ ПРИЗНАКОВ, ПОДЧИНЯЮЩИХСЯ НОРМАЛЬНОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ, ДОСТОВЕРНОСТЬ РАЗЛИЧИЯ ДВУХ СРЕДНИХ ВЕЛИЧИН ОПРЕДЕЛЯЕТСЯ С ПОМОЩЬЮ …

1) ошибки репрезентативности

2) коэффициента вариации

3) средней арифметической

4) критерия Стьюдента

Решение: для признаков, подчиняющихся нормальному закону распределения, достоверность различия двух средних величин определяется с помощью критерия Стьюдента.

Правильный ответ: 4.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 78.

6.136. Статистическая достоверность различия между двумя средними величинами определяется с помощью …

1) ошибки репрезентативности

2) коэффициента вариации

3) среднего квадратического отклонения

4) критерия Стьюдента

Решение:статистическая достоверность различия между двумя средними величинами определяется с помощью критерия Стьюдента.

Правильный ответ: 4.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 81.

6.137. Критерий достоверности Стьюдента указывает …

1) во сколько раз разность сравниваемых средних величин превышает их среднюю ошибку

2) во сколько раз среднее квадратическое отклонение меньше средней арифметической

3) на ошибку разности средних величин в генеральной и выборочной совокупности

Решение:критерий достоверности Стьюдента указывает во сколько раз разность сравниваемых средних величин превышает их среднюю ошибку.

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 80.

6.138. Величина критерия достоверности Стьюдента при сравнении средних величин определяется по формуле …

1)

2)

3)

4)

Решение: величина критерия достоверности Стьюдента при сравнении средних величин определяется по формуле: .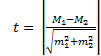

Правильный ответ: 4.

Литература: Общественное здоровье и здравоохранение, экономика здравоохранения: учебник: в 2 т. / под ред. В. З. Кучеренко – М.: ГЕОТАР-Медиа, 2013, стр. 92.

6.139. Расчет критерия достоверности Стьюдента при сравнении относительных величин производится по формуле …

1)

2)

3)

4)

Решение: расчет критерия достоверности Стьюдента при сравнении относительных величин производится по формуле: .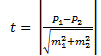

Правильный ответ: 4.

Литература: Общественное здоровье и здравоохранение, экономика здравоохранения: учебник: в 2 т. / под ред. В. З. Кучеренко – М.: ГЕОТАР-Медиа, 2013, стр. 92.

6.140. ФОРМУЛА ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТ СТЬЮДЕНТА …

1)

2)

3)

4)

Решение: формула вычисления коэффициента достоверности Стьюдента: .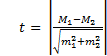

Правильный ответ: 4.

Литература: Общественное здоровье и здравоохранение, экономика здравоохранения: учебник: в 2 т. / под ред. В. З. Кучеренко – М.: ГЕОТАР-Медиа, 2013, стр. 92.

6.141. Вывод, который можно сделать о наличии статистической достоверности различий между двумя выборочными совокупностями, если критерий достоверности Стьюдента превышает значение 2 (при n>30) …

1) выявленные различия случайны

2) выявленные различия не случайны

Решение: если при сравнении двух выборочных совокупностей критерий достоверности Стьюдента превышает значение 2 (при n>30), можно сделать вывод о достоверном различии между ними с вероятностью 95,5%, т.е. выявленные различия не случайны.

Правильный ответ: 2.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77-82.

6.142. РАЗЛИЧИЯ МЕЖДУ СРЕДНИМИ ВЕЛИЧИНАМИ ДВУХ ПРИЗНАКОВ ЯВЛЯЮТСЯ СУЩЕСТВЕННЫМИ, ЕСЛИ ВЕЛИЧИНА критерия стьюдента (t) больше или РАВНА:

Решение: если при сравнении двух выборочных совокупностей критерий достоверности Стьюдента превышает значение 2 (при n>30), можно сделать вывод о достоверном различии между ними с вероятностью 95,5%.

Правильный ответ: 4, 5.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77-82.

6.143. ПРИ ЗНАЧЕНИИ t-КРИТЕРИЯ (СТЬЮДЕНТА) БОЛЬШЕ ИЛИ РАВНОМ 2 РАЗЛИЧИЯ ДВУХ СРЕДНИХ ВЕЛИЧИН …

Решение: если при сравнении двух выборочных совокупностей критерий достоверности Стьюдента превышает значение 2 (при n>30), можно сделать вывод о достоверном различии между ними с вероятностью 95,5%.

Правильный ответ: 1.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77-82.

6.144. СОБЫТИе В МЕДИКО-БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ СЧИТАЕТСЯ НЕ ДОСТОВЕРНым, ЕСЛИ его ВЕРОЯТНОСТи РАВНы:

Решение: событие в медико-биологических исследованиях считается не достоверным, если вероятность его прогноза меньше 95,5%.

Правильный ответ: 1, 4.

Литература: Полунина М.В. Общественное здоровье и здравоохранение: Учебник: – М.: Издательство «Медицинское информационное агентство», 2010, стр. 77-82.

6.145. критерий соответствия хи-квадрат используется в случае …

1) в случае сопоставления неоднородных совокупностей

2) когда нет необходимости знать средние или относительные величины для оценки достоверности различий вариационных рядов

3) когда необходимо оценить степень влияния факторов на результирующий признак

4) поиска взаимосвязи между признаками

Решение: критерий соответствия хи-квадрат используется в случае когда нет необходимости знать средние или относительные величины для оценки достоверности различий вариационных рядов.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник