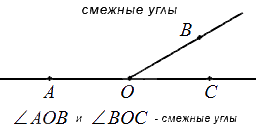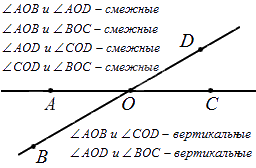Чем мерить градусы в геометрии
Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
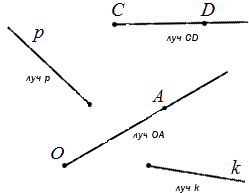
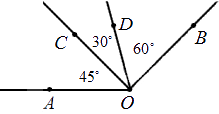
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
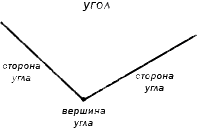
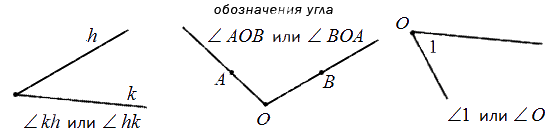
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
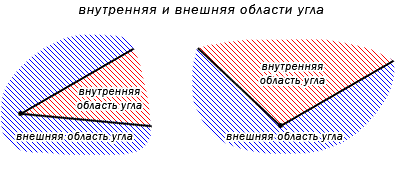
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
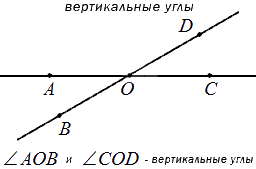
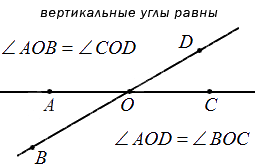
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
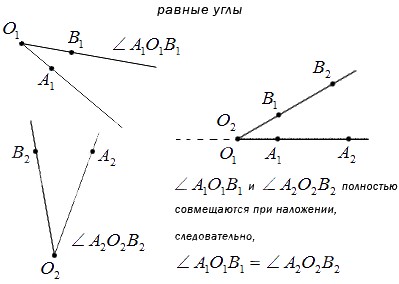
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
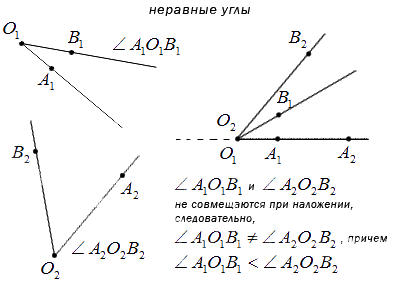
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
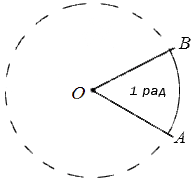
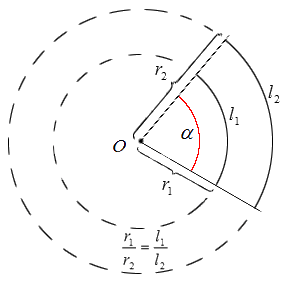
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
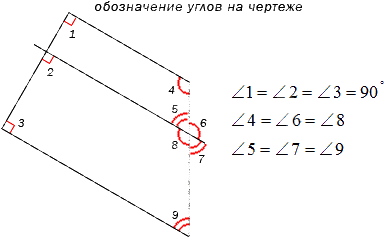
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Измерение углов
Андрей Андреев, Полина Ачева, Алексей Панов
«Квантик» №12, 2020
В школьной геометрии угол — это фигура, состоящая из двух лучей, выходящих из одной точки (рис. 1). Эта точка называется вершиной угла, а лучи — его сторонами. Угол разбивает плоскость на две части: на рисунке 2 они окрашены в зелёный и жёлтый цвет. Эти части называются плоскими углами.
Измерить угол можно обычным транспортиром, который размечен в градусах от 0° до 180° (рис. 3, слева).
Рис. 2 (слева). Два плоских угла — зелёный и жёлтый. Рис. 3. Транспортиры — полукруговой и круговой
Плоские углы удобно измерять круговым транспортиром, размеченным от 0° до 360° (рис. 3, справа). Конечно, для научных и технических измерений углов нужны более точные приборы: например, такие, как на рисунке 4. Слева там изображён один из астрономических инструментов Тихо Браге, с которым он проводил свои высокоточные наблюдения. Результаты этих наблюдений позволили Кеплеру вывести законы движения планет. Справа — современный электронный теодолит, используемый в геодезии.
Рис. 4. Секстант Тихо Браге и современный теодолит
А можно ли измерять углы, не применяя вообще никаких инструментов?
«Ручное измерение» углов. Об этом методе мы прочли в книге «Музыка сфер. Математика и астрономия», написанной Розой Марией Рос. Цитируем:
. Существует очень простой, хотя и не слишком точный, способ измерения углов вручную. Если мы вытянем руку перед собой, то растопыренная ладонь будет указывать интервал в 20°, кулак — 10°, большой палец — 2°, мизинец — 1°. Этот способ могут использовать и взрослые, и дети, так как размеры ладони человека увеличиваются пропорционально длине его руки.
Поясним сказанное. Пусть мы наблюдаем за двумя звёздами, расположенными на небе недалеко друг от друга. Направление взгляда на каждую из них задаёт луч. Угол между этими двумя лучами (с вершиной в глазу наблюдателя) мы и хотим измерить. Его величина называется угловым расстоянием между звёздами. Вытянем правую руку с растопыренной ладонью, как на рисунке 5 справа. Если кончик большого пальца закрывает одну звезду, а кончик мизинца — другую, угловое расстояние между звёздами можно оценить в 20°. Прикладывая ладони друг к другу, можно измерять углы до 40° (рис. 5, справа внизу).

Рис. 5. Ручное измерение углов
Задача 1. Звёздной ночью найдите на небе ковш Большой Медведицы (рис. 6) и «вручную» оцените угловое расстояние между звёздами Мерак и Дубхе.
Рис. 6. Ковш Большой Медведицы
Напомним: в направлении Мерак → Дубхе расположена Полярная звезда, указывающая путь на север.
Задача 2. Отыщите на небе Полярную звезду и найдите угловое расстояние между ней и звездой Дубхе.
Решив задачи, вы сможете проверить себя, так как известно, что расстояние Дубхе — Полярная звезда примерно в 5 раз больше расстояния Мерак — Дубхе.
Конечно, ручное измерение углов не позволяет добиться хорошей точности. Сейчас мы опишем бесприборный метод измерения углов, позволяющий проводить измерения со сколь угодно высокой точностью. Начнём с нескольких экспериментов.
Эксперименты с треугольниками: «60°» ≠ 60°. Мы купили несколько одинаковых треугольников, как на рисунке 7. Углы этого треугольника по стандарту должны быть равны 30°, 60° и 90°, но мы хотим проверить, так ли это на самом деле. Начнём со среднего по величине из этих углов, обозначив его α. Итак, верно ли, что α = 60°?
Рис. 8. Каждый треугольник получается из соседнего поворотом на угол α, см. видео
Эксперимент № 1: поворачиваем треугольники. Выложим на плоскость один за другим шесть треугольников, как на рисунке 8: каждый получен из соседнего поворотом на угол α.
Видно, что первый и последний треугольники не сомкнулись, и это означает, что в сумме шесть одинаковых углов α дают меньше 360°, то есть 6α 360°, откуда α > 360°/7. Объединим полученные два неравенства и запишем их в виде
Эксперимент № 2: переворачиваем треугольники. На рисунке 9 представлен другой способ выкладывания треугольников. Каждый треугольник получается из соседнего переворотом вокруг их общей стороны на 180°. Этот способ даёт такую же оценку измеряемого угла, но он будет удобнее для нас в дальнейшем.
Практический совет: чтобы треугольники не смещались при малейшем прикосновении, не укладывайте их на скользкую поверхность. На видео мы воспользовались оборотной стороной коврика для ванной: она сделана из материала, не скользящего даже по влажному гладкому полу ванной комнаты, и идеально подходит для наших экспериментов.
Уменьшаем число треугольников, увеличиваем точность измерения. Первое усовершенствование: будем использовать единственный экземпляр треугольника. Опять обозначим один из его углов через α. Нарисуем на плоскости луч и совместим вершину угла с вершиной луча, а одну из сторон угла направим вдоль луча, как на рисунке 7. Перевернём треугольник вокруг другой стороны угла (не лежащей на луче). Потом перевернём треугольник вокруг другой стороны угла, опять перевернём и т. д., пока максимально не приблизимся к нарисованному лучу. Так мы определим максимальное k, для которого kα 360°, то есть
Задача 4 (Г. Фельдман, Д. Баранов, XXXI Турнир городов). Нарисован угол, и ещё имеется только циркуль.
В пункте б можно обойтись и без циркуля, если есть деревянный угольник с данным углом, о котором мы хотим выяснить, равен ли он 31°.
И напоследок — небольшой список увлекательных книг, в которых обсуждается измерение углов в астрономии и геометрии, с небольшими аннотациями.
Приборы и инструменты для измерения углов
В разное время каждый из нас знакомится с геометрическими, географическими и геодезическими инструментами для измерения углов. Нахождение углов осуществляется при выполнении полевых геодезических, маркшейдерских, изыскательских работ и камеральной обработке измерений.
Измерения углов на плоскости
Наверное, самым первым знакомством из так называемых камеральных инструментов у каждого из нас было знакомство с транспортиром. На профессиональном уровне металлический геодезический транспортир с поперечным масштабом использовался в маркшейдерских отделах шахт и карьеров при выполнении камеральных, проектных и подготовительных работ. С его помощью графическим способом определяют горизонтальные углы и откладывают дирекционные углы при проектировании горных выработок, подготовительных работах для задания им направления на планшетах и планах.
Следующим, применяемым в камеральных условиях геодезическим инструментом можно считать тахеограф. Его используют при графическом оформлении результатов тахеометрической съемки. Он представляет единую конструкцию из круга с градусной шкалой и линейки. С его помощью по дуге вдоль конструкции круга отмечаются значения горизонтальных углов съемочных точек, перенесенных из журнала полевых работ. А расстояния до точек съемки откладывают по линейке в соответствующем масштабе составления плана.
Пространственные измерения углов
Для получения пространственного положения точек местности и отображения их на плоскости в геодезии применяются способы измерения расстояний и углов между ними с помощью различных геодезических приборов.
Качественной характеристикой геодезических и маркшейдерских измерений считается точность их выполнения, которая зависит от многих факторов и аспектов. Одним из них являются средства измерения. Существует своеобразный инженерный подход для выбора соответствующего инструмента требуемой точности работ. Так что все приборы измеряющие углы можно разделить по точности исполнения измерений.
Буссоль и эклиметр
Эти два приспособления могут использоваться в одном виде работ, называемом буссольная съемка (ход). Она применяется в местности, где нет возможности применять теодолитные ходы, тахеометрические съемки. Особую ценность при съемках крутых, круто наклонных и наклонных горных выработок в рудниках имеет подвесная буссоль, используемая до настоящего времени.
Буссолью измеряют магнитные азимуты всех сторон хода, по разности которых можно определить горизонтальные углы. На планах графическим способом выстраивают линии буссольного хода с применением транспортира при откладывании азимутов (или горизонтальных углов) и с использованием поперечного масштаба и циркуля при построении длин линий хода. При прокладывании буссольного хода для получения вертикальных углов между точками используют подвесной эклиметр.
Он представляет собой металлический полукруг со шкалой и отвесом, крепящимся в его центре. При подвешивании полукруга на натянутые между точками хода шнуры берут отсчеты по отвесной линии, проходящей через шкалу эклиметра. Эти отсчеты соответствуют значениям вертикальных углов линий буссольного хода, которые необходимы для определения горизонтальных проложений этих сторон.
Угломеры
Следующим прибором, служащим для измерения углов, применяющимся в маркшейдерском производстве, безусловно, считается угломер горный. Этот инструмент используется для определения линии и формы очистного забоя в подземных горных выработках угольных шахт. Развитие и применение таких приборов проходило на протяжении практически всего советского периода страны, последний из них У-60 выпускался со специальными визирными марками.
Точность измерения углов такими приборами относительно не высокая, но вполне достаточная для тех работ, которые выполняются с их помощью. Зависит она в первую очередь от точности снятия отсчетов и цены деления механической части шкалы, а именно: отсчетного устройства лимба с дополнительными шкалами (нониус, верньер).
Теодолиты и тахеометры
Наиболее широко используемыми инструментами для измерения горизонтальных и вертикальных углов в современной геодезии и маркшейдерии являются теодолиты. Основным критерием, по которому разделяют теодолиты на разные типы, считается точность измерений. Из них можно выделить:
Числовые величины в маркировках современных теодолитов соответствуют значению, с девяноста пяти процентной вероятностью, среднеквадратической погрешности измерения угла.
Известно, что для определения пространственного положения точек используются измерения углов в вертикальной плоскости или как их называют вертикальных углов. Для этого в угломерах, теодолитах конструктивно устроен вертикальный круг измерений. В последние десятилетия технические усовершенствования и технологическое развитие сказалось и на новых устройствах теодолитов. Появились новые модификации и в зависимости от назначения этих устройств выделяют:
Инклинометры
Интересный прибор, связанный с измерительным процессом определения пространственного положения в точках недоступных для измерений другими возможными способами. С его помощью определяют угол наклона (вертикальный угол) и азимут линии в заданном направлении в конкретной точке (точки съемки), например при бурении скважин.
Принципы действия в настоящее время в таких приборах разнообразны. В основе использования простейшего устройства инклинометра ИК-2 стоят три чувствительных элемента, позволяющие определять пространственное положение:
И один элемент в этом приборе позволяет фиксировать азимут и угол наклона, называемый переключающим механизмом.
Не вдаваясь в технические особенности всевозможных видов инклинометров, они в любом случае состоят из двух частей:
Свое применение инклинометры находят в различных отраслях. Они используются при измерениях в глубинных скважинах во время геологической разведки месторождений полезных ископаемых. Были задействованы при установлении и определении положения «скользящей» опалубки на больших высотах при выполнении целого комплекса геодезического обслуживания во время возведения самого высотного небоскреба Бурдж Дубай высотой 828 метра. Так на первых ста пятидесяти шести этажах железобетонной качающейся конструкции башни для измерения ее пространственного положения было установлено восемь двухосевых электронных датчиков инклинометров Leica NIVEL 210. Эти датчики позволили выполнить измерения наклона в двух перпендикулярных осях с точностью 0,2 секунды.
Углы и градусы
Определение величин углов
Первые попытки древних людей измерять земельные участки
(изначально геометрия – это измерение земли) наткнулись на
острую необходимость в угловых измерениях. Крайне редко
их наделы имели правильную форму. Поэтому понятие угла
появилось практически одновременно с линейным отрезком
и/или расстоянием. Другое дело, измерять и тем более
вычислять значения углов люди научились значительно позже.
Хотя уже древние греки оперировали этими понятиями более чем успешно.
Полупрямая (луч) в геометрии определяется как бесконечно длинная
прямая, имеющая начало. Она состоит из всего множества точек,
лежащих на этой линии, включая начальную. Угол же образуют два
луча с совмещенными точками начала. Можно дать и такое
определение этой геометрической фигуры. Причем общую для лучей
точку принято называть вершиной угла, а лучи – сторонами угла.
Удивительно, но размещение точки в любом месте любой прямой
эквивалентно получению двух равновеликих и разнонаправленных
лучей с общим началом. Следовательно, эта нехитрая операция
создает угол как геометрическую фигуру.
Откуда взялся градус
Достоверное происхождение этой угловой меры неизвестно.
Наиболее вероятная гипотеза о делении на 60 частей
угла равностороннего треугольника вавилонянами отлично
согласуется с шести десятеричной системой счисления, принятой
в этом архаичном обществе. Число 60 делится на 2, 3, 5, 6, 10,
15, 30 и, собственно, на 60. Отсюда удобство его применения в
торговле и прочих бытовых отношениях.
Согласно другой версии, окружность разделили на 360 равных
фрагментов по причине равенства их количества числу дней в году.
Персы, например, немало повлиявшие на развитие математики в
целом и геометрии в частности, использовали именно такой календарь.
В любом случае градус используется до сих пор, обозначая 1/360 часть
полного оборота (делит круг на 360 равных секторов). Само слово с
латыни переводится как шаг, ступень, порог. Отсюда слово градуировка,
применимое абсолютно ко всем измерительным приборам.
Для измерения более мелких величин углов используют минуту
и секунду. Эти величины также являются результатом дробления
на 60. Минута делит градус, а секунда минуту. То есть 1 минута
равна 1/60 градуса, а секунда составляет 1/60 минуты или 1/3600 градуса.
Транспортир, знакомый каждому со школьных времен – элементарнейший
инструмент, позволяющий довольно точно измерять или рисовать углы.
Разумеется, в практике промышленности, строительства и других сферах
человеческой деятельности применяются более точные средства,
теодолит, как вариант. Но результат измерения любого современного
инструмента всегда выражается в градусах.
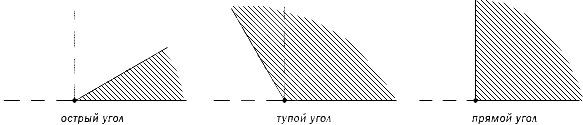
Учитывая простоту фигуры и ее составляющих, углы не отличаются
большим разнообразием. Принято выделять следующие их виды:
Помимо прямого, существует еще несколько частных случаев, а именно:
Геометрия, оставаясь неотъемлемой частью математики,
все же выделена в отдельную дисциплину. Причина
такого подразделения проста. Математическая наука
не терпит даже тени хаоса, что выражается в четкой
классификации ее разделов, но с сохранением
органической связи между собой.
На самом деле, без глубокого знания основ геометрии
практически невозможно изучить смежные математические
дисциплины, такие как тригонометрия, анализ, интегральное
или дифференциальное счисления. Более того, изучение
любой точной науки требует свободного владения
геометрическими понятиями. Механика или оптика
в физике – наиболее яркое тому подтверждение.