Чем можно измерить угол кроме транспортира
Чем заменить транспортир
Транспортир в домашних условиях можно заменить на:
| Чем можно заменить транспортир | Описание |
| Лист бумаги | Идеальный вариант для определения углов 30, 45, 60 градусов. У листика все углы по 90 градусов, если его свернуть вдвое, получится 45. Если его разделить на три части можно получить 30 и 60 градусов. |
Соответственно если 30 сложить пополам получится 15 градусов. Также можно получить и угол в 180 градусов. В других случаях придется использовать транспортир.
Довольно часто у людей возникает вопрос, чем можно заменить транспортир в домашних условиях, поскольку он не всегда оказывается под рукой.
Существует несколько альтернатив, которые позволяют сделать расчеты, однако, нужно учитывать, что все методы могут иметь погрешности, поэтому лучше воспользоваться транспортиром.
Определение угла с помощью листа бумаги
Определить угол в 90, 30, 60 и 45 градусов достаточно просто. Для этого нужно воспользоваться обычным листом бумаги, который уже имеет прямые углы.
Для определения других углов потребуется транспортир.
Листочек в клеточку
На листике в клеточку легко можно сделать замеры тех же стандартных углов, что и в предыдущем варианте.
Полученные углы нужно вырезать и сравнить с заданным углом. Обычно, после прикладывания заготовок, получается, визуально определить примерные показатели.
Механические часы
Циферблат часов будет отличной альтернативой транспортиру. Возможно, такие замеры будут иметь небольшую погрешность, поэтому его лучше использовать только для домашних целей, а не произведения каких-то серьезных измерений.
Часы имеют 60 одинаковых делений, каждое равно 6 градусам. Соответственно половина деления – это 3 градуса, а 1/3 равна двум.
Если получиться поставить часы точно на точку, с которой начинается угол, погрешность окажется незначительной.
Найди идеальную альтернативу транспортиру довольно сложно, однако нет ничего невозможного. Поэтому можно воспользоваться простыми рекомендациями, которые помогут определить необходимый угол.
Но нужно учитывать, что каждый метод имеет свои особенности и не всегда поможет узнать точные цифры. Самой простой заменой транспортиру является подготовленный бумажный трафарет, однако его не всегда есть возможность распечатать.
Средства для измерения углов
Из Википедии — свободной энциклопедии
Средства для измерения углов
Углы изделий измеряют тремя основными методами:
Для хранения и передачи единицы плоского угла, градуировки угломерных приборов, а также для непосредственных измерений служат угловые призматические меры. Они выпускаются в виде наборов плиток толщиной 5 мм с градацией 2 градуса, 1 градус, 1’, 15’’. Набор состоит из 93 плиток с номинальными углами до 90 градусов. Угловые меры изготавливают трех классов точности: 0, 1, 2.
Для проверки и разметки прямых углов, для контроля изделий при сборке или монтаже и т.д. предназначены угольники поверочные.
Для проверки углов конусов служат калибры-втулки (для проверки наружных конусов) и калибры-скобы (для контроля внутренних конических поверхностей).
При абсолютных измерениях величина угла определяется непосредственно в угловых единицах с помощью угломеров, делительных головок, микроскопов и других приборов. Наибольшее распространение получили нониусные угломеры, которые выпускаются двух типов: УН — для измерения наружных и внутренних углов и УМ — для измерения наружных углов. Наружными называются углы 0 – 180 градусов, внутренними — углы больше 180 градусов. Устройство нониуса универсального угломера принципиально ничем не отличается от устройства нониуса штангенинструментов.
Для контроля горизонтальности и вертикальности плоских и цилиндрических поверхностей, а также для оценки углов отклонений реальных поверхностей деталей от заданных применяются различного рода уровни.
Чем можно измерить угол кроме транспортира
«И зачем это учить? Всё равно ведь в жизни не пригодится!». Наверное, в детстве каждый хоть раз задавал себе этот вопрос, сидя на скучнейшем из уроков. Но нет в мире бесполезных знаний. А многое из «ненужной» школьной информации оказывается весьма полезным во взрослом быту. К примеру вот эти 8 школьных хитростей, которые не помешает вспомнить всем.
Эти факты и навыки многие из нас изучали в школе, но наверняка забыли, едва покинув школьные стены. Пришло время приоткрыть «чертоги памяти» и достать из них немного старых-новых, но одинаково полезных знаний.
1. Как рассчитать время, оставшееся до заката
Когда солнце уже клонится к горизонту, поднимите ладонь горизонтально перед глазами. Сделайте так, чтобы солнечный диск «касался» указательного пальца. Теперь пересчитайте количество пальцев от солнца до горизонта (можно подставить и вторую ладонь снизу). Каждый из них равен примерно 15 минутам. К примеру, 4 пальца между солнцем и горизонтом – это 1 час до заката. Весьма полезная скаутская хитрость, которая здорово пригодится в походе, на рыбалке или когда хочется удивить девушку на романтичном свидании.
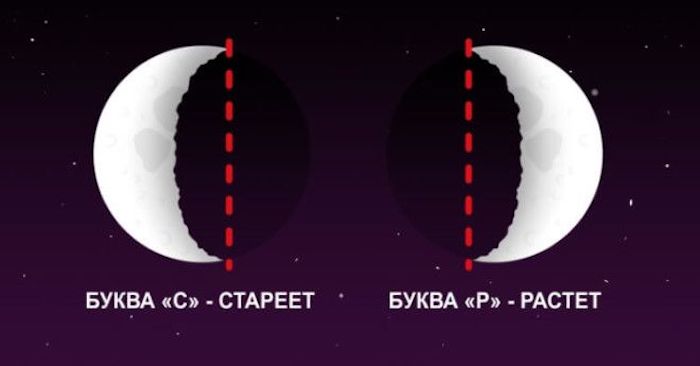
2. Как понять, луна возрастает или убывает
Нужно мысленно соединить углы полумесяца вертикальной линией. Если в итоге луна похожа на букву «С», то она убывает (можно запомнить, как «С = Стареет»), а если на букву «Р» – растёт.
3. Разбираться в римских цифрах не хуже самих древних римлян
Римские цифры для современного человека – немногим проще клинописи. Уложить в голове основы нумерации поможет мнемоническое правило. Прочтите и запомните вот такую странную фразу: «Мы Dарим Сочные Lимоны, Хватит Vсем Iх». Первая буква каждого из слов – это цифра (в порядке убывания): М = 1000, D = 500, C = 100, L = 50, X = 10, V = 5, I = 1. Неплохая подсказка для живущих в MMXVIII.
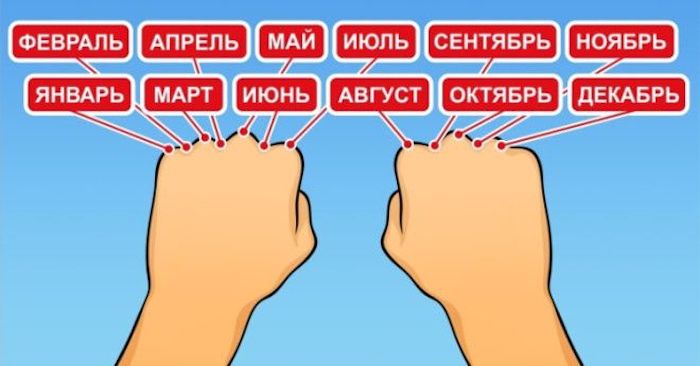
4. Перестать угадывать, в этом месяце 30 или 31 день
Вы точно слышали об этом трюке в школе. Обе ладони – в кулаки и начинайте считать костяшки. Каждая костяшка и каждая впадина – это месяц. Начинаем, естественно, с января. Костяшка = 31 день, а впадина = 30. Ах да, сколько там дней в феврале?
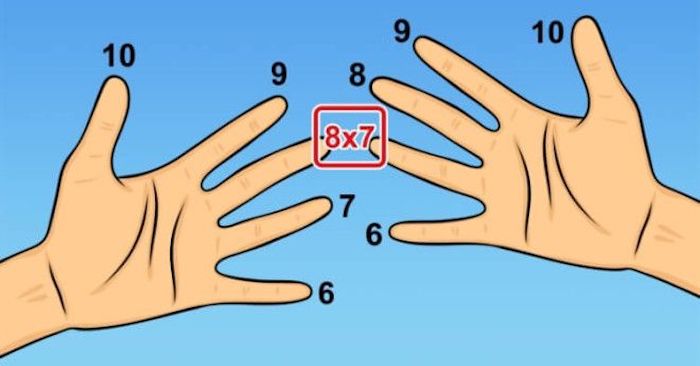
5. Как умножать на пальцах
Таблица умножения – та ещё морока, особенно, когда переваливает за 5. Но если провал в школьных знаниях настойчиво даёт о себе знать, всегда можно перемножить числа от 6 до 9 на пальцах. Для этого внимательно посмотрите на свои руки, опустив их ладонями вниз. Пронумеруйте каждый палец от 6 до 10, начиная с мизинца. Теперь, чтобы умножить, к примеру, 8 на 7, соедините «восьмой» палец одной руки с «семёркой» другой (как на фото). Все пальцы, которые оказались снизу и сами соединённые – это десятки. В нашем случае, «5». А пальцы сверху – это единицы и их количество нужно умножить друг на друга. В данном примере это 2 х 3 =6. Итого: 56.
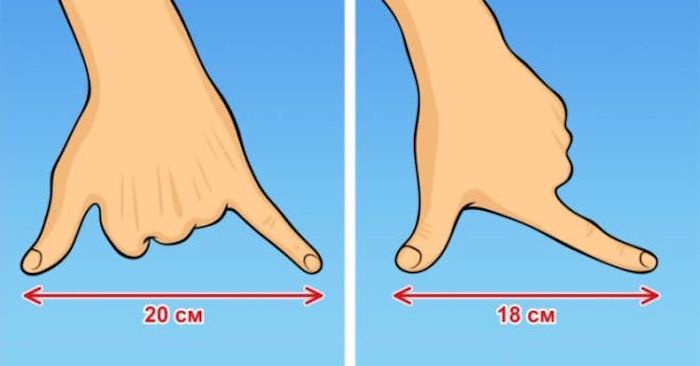
6. Измерить длину небольших предметов без линейки
Тут тоже можно посчитать «на пальцах». Достаточно запомнить, что расстояние между кончиками большого и указательного пальцев равно примерно 18 см, а между большим и мизинцем – около 20. Конечно, в силу «индивидуальных настроек» (читай, размеров) каждого результат никогда не будет точным до миллиметра. Но хоть примерно угадаете.
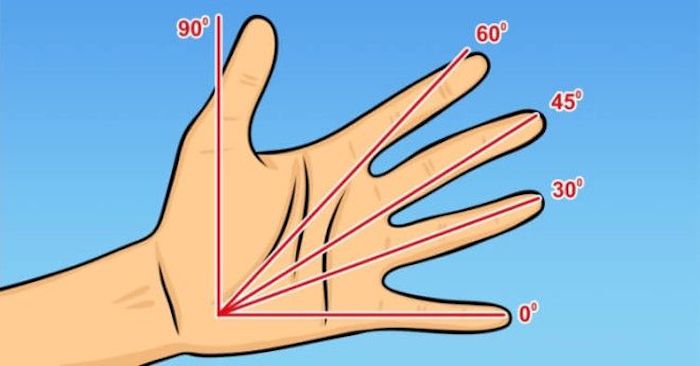
7. И измерить угол без транспортира
Транспортир – второй после циркуля предмет, который каждый третий стабильно забывал положить в портфель и принести на геометрию. Но и без него можно выкрутиться. Если запомнить, что угол между большим пальцем и мизинцем в «нормально растопыренном» положении = 90 градусов, между мизинцем и безымянным = 30 градусов, мизинцем и средним = 45, а мизинцем и указательным = 60.
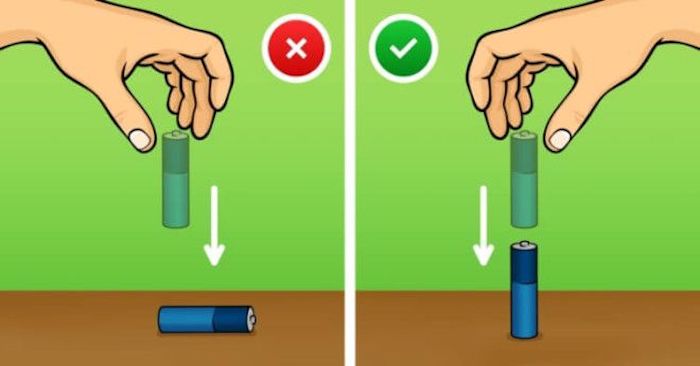
8. Проверить, заряжена ли батарейка
Тест по физике для 7-го класса: уроните батарейку с маленькой высоты, удерживая её строго вертикально. Упала набок – разряжена. А если отскочила, но сохранила вертикальное положение – ещё поработает.
Если вам понравился пост, пожалуйста, поделитесь им со своими друзьями:
И не забудьте:

Приборы и инструменты для измерения углов
В разное время каждый из нас знакомится с геометрическими, географическими и геодезическими инструментами для измерения углов. Нахождение углов осуществляется при выполнении полевых геодезических, маркшейдерских, изыскательских работ и камеральной обработке измерений.
Измерения углов на плоскости
Наверное, самым первым знакомством из так называемых камеральных инструментов у каждого из нас было знакомство с транспортиром. На профессиональном уровне металлический геодезический транспортир с поперечным масштабом использовался в маркшейдерских отделах шахт и карьеров при выполнении камеральных, проектных и подготовительных работ. С его помощью графическим способом определяют горизонтальные углы и откладывают дирекционные углы при проектировании горных выработок, подготовительных работах для задания им направления на планшетах и планах.
Следующим, применяемым в камеральных условиях геодезическим инструментом можно считать тахеограф. Его используют при графическом оформлении результатов тахеометрической съемки. Он представляет единую конструкцию из круга с градусной шкалой и линейки. С его помощью по дуге вдоль конструкции круга отмечаются значения горизонтальных углов съемочных точек, перенесенных из журнала полевых работ. А расстояния до точек съемки откладывают по линейке в соответствующем масштабе составления плана.
Пространственные измерения углов
Для получения пространственного положения точек местности и отображения их на плоскости в геодезии применяются способы измерения расстояний и углов между ними с помощью различных геодезических приборов.
Качественной характеристикой геодезических и маркшейдерских измерений считается точность их выполнения, которая зависит от многих факторов и аспектов. Одним из них являются средства измерения. Существует своеобразный инженерный подход для выбора соответствующего инструмента требуемой точности работ. Так что все приборы измеряющие углы можно разделить по точности исполнения измерений.
Буссоль и эклиметр
Эти два приспособления могут использоваться в одном виде работ, называемом буссольная съемка (ход). Она применяется в местности, где нет возможности применять теодолитные ходы, тахеометрические съемки. Особую ценность при съемках крутых, круто наклонных и наклонных горных выработок в рудниках имеет подвесная буссоль, используемая до настоящего времени.
Буссолью измеряют магнитные азимуты всех сторон хода, по разности которых можно определить горизонтальные углы. На планах графическим способом выстраивают линии буссольного хода с применением транспортира при откладывании азимутов (или горизонтальных углов) и с использованием поперечного масштаба и циркуля при построении длин линий хода. При прокладывании буссольного хода для получения вертикальных углов между точками используют подвесной эклиметр.
Он представляет собой металлический полукруг со шкалой и отвесом, крепящимся в его центре. При подвешивании полукруга на натянутые между точками хода шнуры берут отсчеты по отвесной линии, проходящей через шкалу эклиметра. Эти отсчеты соответствуют значениям вертикальных углов линий буссольного хода, которые необходимы для определения горизонтальных проложений этих сторон.
Угломеры
Следующим прибором, служащим для измерения углов, применяющимся в маркшейдерском производстве, безусловно, считается угломер горный. Этот инструмент используется для определения линии и формы очистного забоя в подземных горных выработках угольных шахт. Развитие и применение таких приборов проходило на протяжении практически всего советского периода страны, последний из них У-60 выпускался со специальными визирными марками.
Точность измерения углов такими приборами относительно не высокая, но вполне достаточная для тех работ, которые выполняются с их помощью. Зависит она в первую очередь от точности снятия отсчетов и цены деления механической части шкалы, а именно: отсчетного устройства лимба с дополнительными шкалами (нониус, верньер).
Теодолиты и тахеометры
Наиболее широко используемыми инструментами для измерения горизонтальных и вертикальных углов в современной геодезии и маркшейдерии являются теодолиты. Основным критерием, по которому разделяют теодолиты на разные типы, считается точность измерений. Из них можно выделить:
Числовые величины в маркировках современных теодолитов соответствуют значению, с девяноста пяти процентной вероятностью, среднеквадратической погрешности измерения угла.
Известно, что для определения пространственного положения точек используются измерения углов в вертикальной плоскости или как их называют вертикальных углов. Для этого в угломерах, теодолитах конструктивно устроен вертикальный круг измерений. В последние десятилетия технические усовершенствования и технологическое развитие сказалось и на новых устройствах теодолитов. Появились новые модификации и в зависимости от назначения этих устройств выделяют:
Инклинометры
Интересный прибор, связанный с измерительным процессом определения пространственного положения в точках недоступных для измерений другими возможными способами. С его помощью определяют угол наклона (вертикальный угол) и азимут линии в заданном направлении в конкретной точке (точки съемки), например при бурении скважин.
Принципы действия в настоящее время в таких приборах разнообразны. В основе использования простейшего устройства инклинометра ИК-2 стоят три чувствительных элемента, позволяющие определять пространственное положение:
И один элемент в этом приборе позволяет фиксировать азимут и угол наклона, называемый переключающим механизмом.
Не вдаваясь в технические особенности всевозможных видов инклинометров, они в любом случае состоят из двух частей:
Свое применение инклинометры находят в различных отраслях. Они используются при измерениях в глубинных скважинах во время геологической разведки месторождений полезных ископаемых. Были задействованы при установлении и определении положения «скользящей» опалубки на больших высотах при выполнении целого комплекса геодезического обслуживания во время возведения самого высотного небоскреба Бурдж Дубай высотой 828 метра. Так на первых ста пятидесяти шести этажах железобетонной качающейся конструкции башни для измерения ее пространственного положения было установлено восемь двухосевых электронных датчиков инклинометров Leica NIVEL 210. Эти датчики позволили выполнить измерения наклона в двух перпендикулярных осях с точностью 0,2 секунды.
Измерение углов
Андрей Андреев, Полина Ачева, Алексей Панов
«Квантик» №12, 2020
В школьной геометрии угол — это фигура, состоящая из двух лучей, выходящих из одной точки (рис. 1). Эта точка называется вершиной угла, а лучи — его сторонами. Угол разбивает плоскость на две части: на рисунке 2 они окрашены в зелёный и жёлтый цвет. Эти части называются плоскими углами.
Измерить угол можно обычным транспортиром, который размечен в градусах от 0° до 180° (рис. 3, слева).
Рис. 2 (слева). Два плоских угла — зелёный и жёлтый. Рис. 3. Транспортиры — полукруговой и круговой
Плоские углы удобно измерять круговым транспортиром, размеченным от 0° до 360° (рис. 3, справа). Конечно, для научных и технических измерений углов нужны более точные приборы: например, такие, как на рисунке 4. Слева там изображён один из астрономических инструментов Тихо Браге, с которым он проводил свои высокоточные наблюдения. Результаты этих наблюдений позволили Кеплеру вывести законы движения планет. Справа — современный электронный теодолит, используемый в геодезии.
Рис. 4. Секстант Тихо Браге и современный теодолит
А можно ли измерять углы, не применяя вообще никаких инструментов?
«Ручное измерение» углов. Об этом методе мы прочли в книге «Музыка сфер. Математика и астрономия», написанной Розой Марией Рос. Цитируем:
. Существует очень простой, хотя и не слишком точный, способ измерения углов вручную. Если мы вытянем руку перед собой, то растопыренная ладонь будет указывать интервал в 20°, кулак — 10°, большой палец — 2°, мизинец — 1°. Этот способ могут использовать и взрослые, и дети, так как размеры ладони человека увеличиваются пропорционально длине его руки.
Поясним сказанное. Пусть мы наблюдаем за двумя звёздами, расположенными на небе недалеко друг от друга. Направление взгляда на каждую из них задаёт луч. Угол между этими двумя лучами (с вершиной в глазу наблюдателя) мы и хотим измерить. Его величина называется угловым расстоянием между звёздами. Вытянем правую руку с растопыренной ладонью, как на рисунке 5 справа. Если кончик большого пальца закрывает одну звезду, а кончик мизинца — другую, угловое расстояние между звёздами можно оценить в 20°. Прикладывая ладони друг к другу, можно измерять углы до 40° (рис. 5, справа внизу).

Рис. 5. Ручное измерение углов
Задача 1. Звёздной ночью найдите на небе ковш Большой Медведицы (рис. 6) и «вручную» оцените угловое расстояние между звёздами Мерак и Дубхе.
Рис. 6. Ковш Большой Медведицы
Напомним: в направлении Мерак → Дубхе расположена Полярная звезда, указывающая путь на север.
Задача 2. Отыщите на небе Полярную звезду и найдите угловое расстояние между ней и звездой Дубхе.
Решив задачи, вы сможете проверить себя, так как известно, что расстояние Дубхе — Полярная звезда примерно в 5 раз больше расстояния Мерак — Дубхе.
Конечно, ручное измерение углов не позволяет добиться хорошей точности. Сейчас мы опишем бесприборный метод измерения углов, позволяющий проводить измерения со сколь угодно высокой точностью. Начнём с нескольких экспериментов.
Эксперименты с треугольниками: «60°» ≠ 60°. Мы купили несколько одинаковых треугольников, как на рисунке 7. Углы этого треугольника по стандарту должны быть равны 30°, 60° и 90°, но мы хотим проверить, так ли это на самом деле. Начнём со среднего по величине из этих углов, обозначив его α. Итак, верно ли, что α = 60°?
Рис. 8. Каждый треугольник получается из соседнего поворотом на угол α, см. видео
Эксперимент № 1: поворачиваем треугольники. Выложим на плоскость один за другим шесть треугольников, как на рисунке 8: каждый получен из соседнего поворотом на угол α.
Видно, что первый и последний треугольники не сомкнулись, и это означает, что в сумме шесть одинаковых углов α дают меньше 360°, то есть 6α 360°, откуда α > 360°/7. Объединим полученные два неравенства и запишем их в виде
Эксперимент № 2: переворачиваем треугольники. На рисунке 9 представлен другой способ выкладывания треугольников. Каждый треугольник получается из соседнего переворотом вокруг их общей стороны на 180°. Этот способ даёт такую же оценку измеряемого угла, но он будет удобнее для нас в дальнейшем.
Практический совет: чтобы треугольники не смещались при малейшем прикосновении, не укладывайте их на скользкую поверхность. На видео мы воспользовались оборотной стороной коврика для ванной: она сделана из материала, не скользящего даже по влажному гладкому полу ванной комнаты, и идеально подходит для наших экспериментов.
Уменьшаем число треугольников, увеличиваем точность измерения. Первое усовершенствование: будем использовать единственный экземпляр треугольника. Опять обозначим один из его углов через α. Нарисуем на плоскости луч и совместим вершину угла с вершиной луча, а одну из сторон угла направим вдоль луча, как на рисунке 7. Перевернём треугольник вокруг другой стороны угла (не лежащей на луче). Потом перевернём треугольник вокруг другой стороны угла, опять перевернём и т. д., пока максимально не приблизимся к нарисованному лучу. Так мы определим максимальное k, для которого kα 360°, то есть
Задача 4 (Г. Фельдман, Д. Баранов, XXXI Турнир городов). Нарисован угол, и ещё имеется только циркуль.
В пункте б можно обойтись и без циркуля, если есть деревянный угольник с данным углом, о котором мы хотим выяснить, равен ли он 31°.
И напоследок — небольшой список увлекательных книг, в которых обсуждается измерение углов в астрономии и геометрии, с небольшими аннотациями.