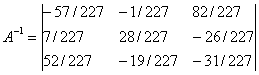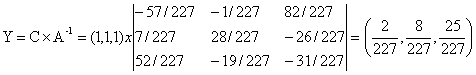Чем можно задать матричную игру
Пример решения матричной игры методом линейного программирования
Решение находим через сервис матричная игра.
| A/B | B 1 | B 2 | B 3 | a = min(Ai) |
| A 1 | 6 | 5 | 7 | 5 |
| A 2 | 10 | 4 | 7 | 4 |
| A 3 | 13 | 10 | 4 | 4 |
| A 4 | 7 | 11 | 5 | 5 |
| b = max(Bi ) | 13 | 11 | 7 | 0 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 5, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 7.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 5 = 1
5x1+4x2+10x3+11x4 >= 1
7x1+7x2+4x3+5x4 >= 1
F(x) = x1+x2+x3+x4 = min
найти максимум функции Ф(y) при ограничениях:
6y1+5y2+7y3 1
В столбце свободных членов есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его строке – любой отрицательный. Взяв этот элемент в качестве разрешающего пересчитаем таблицу.
В качестве ведущего выберем столбец, соответствующий переменной x1.
1-ая строка является ведущей.
| План | Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| x 1 | 1 / 6 | 1 | 1 2 / 3 | 2 1 / 6 | 1 1 / 6 | -1 / 6 | 0 | 0 | |
| x 6 | -1 / 6 | 0 | 4 1 / 3 | 5 / 6 | -5 1 / 6 | -5 / 6 | 1 | 0 | |
| x 7 | 1 / 6 | 0 | 4 2 / 3 | 11 1 / 6 | 3 1 / 6 | -1 1 / 6 | 0 | 1 | |
| Индексная строка | F(X) | -1 / 6 | 0 | -2 / 3 | -1 1 / 6 | -1 / 6 | 1 / 6 | 0 | 0 |
Первый способ нахождений двойственной задачи
Второй способ нахождений двойственной задачи
Решение матричной игры симплексным методом
Решение проводим с помощью калькулятора.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 0 | 3 | 1 | 0 |
| A2 | 3 | 0 | 5 | 0 |
| A3 | 2 | 1 | 1 | 1 |
| b = max(Bi ) | 3 | 3 | 5 | 0 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 1, которая указывает на максимальную чистую стратегию A3.
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a<>b, тогда цена игры находится в пределах 1 = 1
3x1+x3 >= 1
x1+5x2+x3 >= 1
F(x) = x1+x2+x3 = min
найти максимум функции Ф(y) при ограничениях:
3y2+y3 1 /3, x1 = 1 /3, x6 = 1
F(X) = 1• 1 /3 + 1• 1 /3 = 2 /3
Оптимальный план двойственной задачи равен:
y1 = 1 /3, y2 = 1 /3, y3 = 0
Z(Y) = 1* 1 /3+1* 1 /3+1*0 = 2 /3
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 2 /3 = 1 1 /2
Оптимальная стратегия игрока А: P( 1 /2 ; 1 /2; 0)
Оптимальная стратегия игрока B: Q( 1 /2; 1 /2; 0)
Решение матричной игры находим через сервис решение матричной игры.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 2, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a<>b, тогда цена игры находится в пределах 2 = 1
3x1+2x2+3x3 >= 1
2x1+x2+3x3 >= 1
F(x) = x1+x2+x3 = min
найти максимум функции Ф(y) при ограничениях:
2y1+3y2+2y3 3 /11, x5 = 2 /11, x2 = 2 /11
F(X) = 1• 3 /11 + 1• 2 /11 = 5 /11
Оптимальный план двойственной задачи равен: y1 = 2 /11, y2 = 0, y3 = 3 /11
Z(Y) = 1* 2 /11+1*0+1* 3 /11 = 5 /11
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков: pi = g*xi; qi = g*yi.
Цена игры: g = 1 : 5 /11 = 2 1 /5
p1 = 2 1 /5•0 = 0
p2 = 2 1 /5• 2 /11 = 2 /5
p3 = 2 1 /5• 3 /11 = 3 /5
q1 = 2 1 /5• 2 /11 = 2 /5
q2 = 2 1 /5•0 = 0
q3 = 2 1 /5• 3 /11 = 3 /5
Оптимальная стратегия игрока А: P( 0; 2 /5; 3 /5)
Оптимальная стратегия игрока B: Q( 2 /5;0; 3 /5)
Матричные игры
В математике под матричными играми понимается игра двух лиц с нулевой суммой, имеющих конечное число стратегий. Выигрыш определяется матрицей игры (матрицей платежей), она же является Нормальной формой игры.
Матричная игра и линейное программирование
Пусть матричная игра задана множеством стратегий первого игрока 
, множеством стратегий второго игрока 
и матрицей платежей 
.
Рассмотрим две задачи линейного программирования
Найти максимум 
Задача 2 (двойственная)
Найти минимум 
Известно, что следующие утверждения эквивалентны
1. Матричная игра имеет положительную цену игры
2. Задачи 1 и 2 разрешимы, при этом, если 
– цена игры,
и 
– оптимальные решения,
то 
и , 
будут оптимальными смешанными стратегиями игроков.
Ссылки
1. Карлин С. Математические методы в теории игр, программировании и экономике М., «Мир», 1964
2. Оуэн Г. Теория игр. М. «Мир», М., 1971
Полезное
Смотреть что такое «Матричные игры» в других словарях:
Матричные игры — [matrix games] класс антагонистических игр, в которых участвуют два игрока, причем каждый игрок располагает конечным числом стратегий. Если один игрок имеет m стратегий, а второй n, то можно построить матрицу игры размерностью m х n. М.и.… … Экономико-математический словарь
матричные игры — Класс антагонистических игр, в которых участвуют два игрока, причем каждый игрок располагает конечным числом стратегий. Если один игрок имеет m стратегий, а второй n, то можно построить матрицу игры размерностью m х n. М.и. могут иметь седловую… … Справочник технического переводчика
Матричные игры — понятие игр теории (См. Игр теория). М. и. игры, в которых участвуют два игрока (I и II) с противоположными интересами, причём каждый игрок имеет конечное число чистых стратегий (См. Стратегия). Если игрок I имеет m стратегий, а игрок II… … Большая советская энциклопедия
Антагонистические игры — (матем.) понятие теории игр (см. Игр теория). А. и. игры, в которых участвуют два игрока (обычно обозначаемые I и II) с противоположными интересами. Для А. и. характерно, что выигрыш одного игрока равен проигрышу другого и наоборот,… … Большая советская энциклопедия
Игра — [game] формализованное описание (модель) конфликтной ситуации[1], включающее четко определенные правила действий участников (игроков), добивающихся выигрыша в результате принятия той или иной стратегии. Это основное понятие теории игр удобно… … Экономико-математический словарь
игра — матч Две команды, играющие определенное количество эндов с целью выявления победителя. [Департамент лингвистических услуг Оргкомитета «Сочи 2014». Глоссарий терминов] игра Формализованное описание (модель) конфликтной ситуации[1],… … Справочник технического переводчика
ИГР ТЕОРИЯ — раздел математики, предметом которого является анализ принятия оптимальных решений в условиях конфликта. Возникнув из задач классической теории вероятностей, теория игр превратилась в самостоятельный раздел в 1945 1955. Таким образом, теория игр… … Энциклопедия Кольера
Игр теория — раздел математики, изучающий формальные модели принятия оптимальных решений в условиях конфликта. При этом под конфликтом понимается явление, в котором участвуют различные стороны, наделённые различными интересами и возможностями выбирать … Большая советская энциклопедия
ТЕОРИЯ ИГР — теория матем. моделей принятия решений в условиях неопределенности, когда принимающий решение субъект ( и г p о к ) располагает информацией лишь о множестве возможных ситуаций, в одной из к рых он в действительности находится, о множестве решений … Философская энциклопедия
М — Магистраль [turnpike] Мажоритарный акционер (Majority shareholder) Мажоритарная доля собственности (majority interest) Мажоритарный контроль (majority control) … Экономико-математический словарь