Чем знаменит математик тарталья
Тарталья, Никколо
Содержание
Биография
Родился в Брешии. Истинная фамилия — Фонтана (Fontana). Отца своего он звал по имени Micheletto (Микелетто). В 1512 году, во время взятия Брешии французами, когда он с матерью спасался в соборе, он получил рану в нижнюю часть лица, вследствие которой произношение его стало неправильным. Поэтому товарищи прозвали его заикой (tartaglia) и прозвище это сделалось его фамилией.
14-ти лет он был отдан в обучение публичному писцу, но так как мать его не могла аккуратно платить учителю, то Тарталья должен был прекратить учение в самом начале. Обладая большой настойчивостью и терпением, он научился читать сам. Пристрастившись к математике, он достиг того, что стал сам преподавать другим и впоследствии стал известным математиком своего времени. Преподавал он в Вероне, Брешии и Венеции.
Учеником Тартальи был другой выдающийся учёный эпохи Возрождения — Джамбатиста Бенедетти.
Научная деятельность
В оставленных Тартальей сочинениях он рассматривает не только вопросы математики, но и некоторые вопросы практической механики, баллистики и топографии. Так, в первом из его сочинений, «Nuova scienza» (1537), он впервые рассматривает вопрос о траектории выпущенного снаряда, причём утверждает, что траектория эта на всём её протяжении есть кривая линия, между тем как до него учили, что траектория снаряда состоит из двух прямых, соединённых кривой линией; тут же он показывает, что наибольшая дальность полёта соответствует углу в 45°; кроме того, в этой книге рассматриваются различные вопросы об измерении поверхности полей.
Вместе с вопросами артиллерии Тарталья занимался также и вопросами укрепления городов и фортификацией вообще и в сочинении «Quesiti et invenzioni diverse» (1546) он предлагает даже особую систему фронта, по начертанию схожего с тенальным; он трактует также о топографической съёмке с помощью буссоли и излагает историю открытия им решения кубических уравнений. В сочинениях «La travagliata invenzione» и «Ragionamenti sopra la Travagliata invenzione» (оба 1551 г.) говорится о разных изобретениях автора, которые он приписывает себе, но все они уже изложены в 1550 г. в книге Кардано «De subtilitate» и принадлежат последнему.
Наиболее обширное сочинение автора называется «Generale trattato de numeri e misure» (1556—1560); в нём подробно рассматриваются многие вопросы арифметики, алгебры и геометрии.
По словам Тартальи, он самостоятельно открыл общий алгоритм решения кубических уравнений, несколько ранее найденный Сципионом дель Ферро. В 1539 году Тарталья передал описание этого метода Дж. Кардано, который поклялся не публиковать его без разрешения Тартальи. Несмотря на обещание, в 1545 году Кардано опубликовал этот алгоритм в работе «Великое искусство», и по этой причине он вошёл в историю математики как «формула Кардано».
СОДЕРЖАНИЕ
Личная жизнь
Биограф Тартальи Арнольдо Масотти пишет, что:
Тарталья зарабатывал себе на жизнь преподаванием практической математики в школах счётов и зарабатывал пенни, где мог:
Этот замечательный человек [Тарталья] был учителем математики-самоучкой, который продавал математические советы артиллеристам и архитекторам, десять пенни за один вопрос, и ему приходилось вести тяжбу со своими клиентами, когда они давали ему потрепанный плащ для его лекций по Евклиду вместо платы. договорились о.
Баллистика
Новая наука (1537) была первой опубликованной работой Тартальи, которую Маттео Валлериани описал как:
. одна из самых фундаментальных работ по механике Возрождения, по сути, первая, которая преобразовала аспекты практических знаний, накопленных ранними современными артиллеристами, в теоретическую и математическую основу.
Тогда господствующая аристотелевская физика предпочла такие категории, как «тяжелый», «естественный» и «сильный», для описания движения, обычно избегая математических объяснений. Тарталья выдвинул математические модели на передний план, «потрошив аристотелевские термины движения снаряда», по словам Мэри Дж. Хеннингер-Фосс. Один из его выводов заключался в том, что максимальная дальность полета снаряда была достигнута при наведении пушки под углом 45 ° к горизонту.
Мэри Дж. Хеннингер-Фосс отмечает, что «труды Тартальи по военной науке имели огромное распространение по всей Европе», являясь справочником для обычных артиллеристов восемнадцатого века, иногда через переводы без указания имени. Он также повлиял на Галилея, который владел «богато аннотированными» копиями его работ по баллистике, когда он приступил к решению проблемы снарядов раз и навсегда.
Переводы
General Trattato di Numeri et Misure
Тарталья послужила примером и в конечном итоге превзошла традицию абакко, которая процветала в Италии с двенадцатого века, традицию конкретной коммерческой математики, преподаваемой в школах абака, поддерживаемых сообществами торговцев. Такие маэстро д’абако, как Тарталья, учили не на счетах, а на бумаге и ручке, внедряя алгоритмы, которые используются сегодня в начальных школах.
лучший трактат по арифметике, появившийся в Италии в его столетие, содержащий очень полное обсуждение числовых операций и коммерческих правил итальянских арифметиков. В этом замечательном произведении изложены жизнь людей, обычаи торговцев и усилия по совершенствованию арифметики в XVI веке.
Часть I занимает 554 страницы и представляет собой коммерческую арифметику, охватывающую такие темы, как основные операции со сложными валютами дня (дукаты, солди, пизолли и т. Д.), Обмен валют, расчет процентов и совместное разделение прибыли. компании. Книга изобилует проработанными примерами с большим упором на методы и правила (то есть алгоритмы), и все они готовы к использованию практически как есть.
В части II рассматриваются более общие арифметические задачи, включая прогрессии, степени, биномиальные разложения, треугольник Тартальи (также известный как «треугольник Паскаля»), вычисления с корнями и пропорциями / дробями.
Часть IV посвящена треугольникам, правильным многоугольникам, Платоновым телам и архимедовым темам, например, квадратуре круга и описанию цилиндра вокруг сферы.
Треугольник Тартальи
Решение кубических уравнений
Объем тетраэдра
Тарталья был великолепным калькулятором и мастером твердой геометрии. В Части IV Общего Траттато он показывает на примере, как вычислить высоту пирамиды на треугольном основании, то есть неправильном тетраэдре.
формула, происходящая из закона косинусов (не то, чтобы он цитировал какое-либо обоснование в этом разделе Общего траттато ).
Объем пирамиды после этого легко получить (не то, что Тарталья дает):
Саймон Стевин изобрел десятичные дроби позже, в шестнадцатом веке, поэтому последняя цифра была чуждой для Тартальи, который всегда использовал дроби. Тем не менее, его подход в некотором роде является современным, предлагая на примере алгоритм вычисления высоты большинства или всех неправильных тетраэдров, но (как обычно для него) он не дает явной формулы.
Тарталья
Полезное
Смотреть что такое «Тарталья» в других словарях:
ТАРТАЛЬЯ — (Tartaglia) Никколо Фонтана (1499 1557), итальянский математик, первый получивший общее решение кубического уравнения вида: х3 + ах2 + bх + с = 0. Его метод был опубликован Джироламо Кардано. С 1534 г. преподавал в Венеции. В соч. «Новая наука»… … Научно-технический энциклопедический словарь
ТАРТАЛЬЯ — (ит. tartaglia). Заика, характерная маска неаполитанской народной комедии. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАРТАЛЬЯ итал. tartaglia. Характерная маска неаполитанской народной комедии. Объяснение… … Словарь иностранных слов русского языка
Тарталья — (итал. Tartaglia) итальянская фамилия или прозвище, дословно переводится как «заика». Известные носители: Тарталья, Никколо (1499 1557) итальянский математик, инженер фортификационных сооружений. Тарталья, Анджело (1370 1421)… … Википедия
Тарталья — (Tartaglia) Никколо (около 1499, Бреша, 13 или 14.12.1557, Венеция), итальянский математик. Труды посвящены вопросам математики, механики, баллистики, геодезии, фортификации и др. В соченении «Новая наука» («Nova scientia. », 1537) он… … Большая советская энциклопедия
ТАРТАЛЬЯ (Tartaglia) Никколо — (ок. 1499 1557) итальянский ученый. Труды по математике, механике, баллистике, геодезии, фортификации и др. Имя Тартальи, наряду с именем Дж. Кардано, связано с разработкой способа решения кубического уравнения … Большой Энциклопедический словарь
Тарталья Никколо — Тарталья (Tartaglia) Никколо (около 1499, Бреша, 13 или 14.12.1557, Венеция), итальянский математик. Труды посвящены вопросам математики, механики, баллистики, геодезии, фортификации и др. В соченении «Новая наука» («Nova scientia. », 1537) он… … Большая советская энциклопедия
Тарталья, Никколо — У этого термина существуют и другие значения, см. Тарталья. Никколо Тарталья. Никколо Тарталья (итал. Niccolò Fontana Tartaglia, 1499 1557) итальянский математик. Содержание 1 Биография … Википедия
Тарталья, Антонио — Антонио Тарталья Гражданство … Википедия
Тарталья (комедия дель арте) — У этого термина существуют и другие значения, см. Тарталья. Тарталья, рисунок Мориса Санда, 1860. Тарталья (итал. Tartaglia, заика) персонаж маска итальянской … Википедия
Тарталья, Марино — Марино Тарталья (хорв. Marino Tartaglia, род. 3 августа 1894 г. Загреб ум. 21 апреля 1984 г. Загреб) хорватский художник и педагог, профессор живописи. Жизнь и творчество Школьное образование получил в Сплите. Живописью… … Википедия
Автор, которого обокрали
«… У меня не было другого наставника, кроме спутника бедности – предприимчивости».
Никколо Тарталья – итальянский математик, инженер фортификационных сооружений, геодезист, имя которого неразрывно связано с разработкой способа решения кубических уравнений в радикалах. О жизни Тарталья известно не очень много. Хотя остались его сочинения, но очень мало сведений о его жизни.
Никколо жил во времена так называемых Итальянских войн (1494-1559), которые вели между собой Франция и Испания за право владеть Италией.
Он лишился отца в раннем детстве, тот был убит при занятии города французскими солдатами (1506).
В 1512 году, во время взятия Брешии французами, когда Никколо с матерью спасался в соборе, он получил рану в нижнюю часть лица, вследствие которой произношение его стало неправильным. Выжил он только благодаря уходу матери. Увечье на вою жизнь лишило его возможности правильно произносить слова, и его стали звать «Тарталья». Тарталья – это прозвище, от итальянского слова tartaglia – заика.
В 14 лет он пошёл к учителю, чтобы выучить алфавит, но у него кончились деньги для оплаты за обучение на букве К. После этого он украл тетрадь с прописями и стал самостоятельно учиться читать и писать, используя из-за отсутствия бумаги в качестве грифельной доски надгробные плиты. Самостоятельно он овладел латинским и греческим языками.
Пристрастившись к математике и самостоятельно овладев ей, он сдал квалификационный экзамен на звание «магистра абака» (что-то вроде учителя арифметики) и стал сам преподавать другим, а впоследствии стал известным математиком своего времени. Преподавал в университетах Вероны, Брешии и Венеции.
В 1534 году, уже имея семью и по-прежнему нуждаясь в деньгах, Тарталья переехал в Венецию, где стал давать публичные уроки математики в церкви Сан-Джаниполо и опубликовал свои научные работы.
Желая прославиться и заработать деньги, Фиоре в 1535 году вызвал на диспут Никколу Тарталью.
Во времена, когда жил Тарталья, обычным делом было проведение научных поединков и турниров, на которых учёные состязались между собой в том, кто быстрее и больше решит задач, предложенных противником. Победитель получал деньги, обретал славу, ему предлагали занять почётную, хорошо оплачиваемую должность.
Никколо узнал, что Фиоре владеет секретом решения кубического уравнения, который ему сообщил его учитель дель Ферро. Тарталья сел за письменный стол и за несколько дней до диспута нашёл способ решения уравнения третьей степени.
Известный врач из Милана Джираломо Кардано в это время писал книгу по математике. Он был разносторонне одарённым учёным: был одновременно математиком и механиком, врачом и алхимиком, хиромантом и личным астрологом римского папы. Он обратился к Тарталье с просьбой сообщить ему формулы для решения уравнений третьей степени или написать в его книге своё собственное добавление на эту тему. Тарталья отказался. Но однажды, будучи в Милане, он открыл Кардано секрет, взяв с него клятву сохранять его. Кардано торжественно поклялся.
Около 1535 г. Тарталья получил кафедру математики в Вероне.
В 1545 году Кардано опубликовал своё «Великое искусство» («Ars magna»), положившее начало современному этапу развития теории уравнений. В предисловии к книге Кардано пишет: «В наше время Сципион дель Ферро открыл формулу, согласно которой куб неизвестного плюс неизвестное равен числу. Это была очень красивая и замечательная работа. Соревнуясь с ним, Никколо Тарталья из Брешии, наш друг, будучи вызван на состязание с учеником дель Ферро по имени Антонио Марио Фиоре, решил, дабы не быть побежденным, ту же самую проблему и после долгих просьб передал её мне».
О Ферро известно немногое, только то, что он жил в 1465-1526 годах, был профессором математики в Болонье с 1496 года. Это – одна из причин того, что Тарталья и Кардано получили славы больше, чем заслуживали.
Опубликованный Кардано в работе «Великое искусство» алгоритм решения уравнений третьей степени вошёл в историю математики как «формула Кардано».
Вопрос о том, действительно ли Тарталья независимо открыл метод дель Ферро, неоднократно обсуждался. Высказывалось предположение, что на самом деле Тарталья каким-то образом получил доступ к записям дель Ферро. В качестве косвенных доказательств этой гипотезы историки ссылались на то, что других серьёзных математических достижений у Тартальи не было. Однако прямых свидетельств в пользу указанного предположения найти не удалось.
В книге «Великое искусство» Кардано опубликовал и формулы решения уравнений четвёртой степени, принадлежащие Лодовико Феррари. За несколько лет до этого Кардано взял к себе в дом слугу – 18-летнего бойкого парня Лодовико, у которого оказались блестящие математические способности. Кардано занимался его образованием; Феррари и принадлежит это выдающееся открытие. В восемнадцать лет Феррари стал профессором Миланского университета.
И хотя Кардано честно написал о том, от кого он узнал секрет решения уравнения третьей степени, Тарталья был оскорблён и пребывал в гневе. В адрес Кардано полетели оскорбления и угрозы, тот не ответил.
В конце жизненного пути Кардано написал автобиографическую книгу «О моей жизни», в которой есть такие строчки: «Сознаюсь, что в математике кое-что, но в самом деле ничтожное количество, я заимствовал у брата Никколо». Возможно, его все-таки мучила совесть.
Тарталья написал книгу, изобразив Кардано человеком, лишённым моральных принципов. За своего учителя вступился Феррари. Он вызвал Тарталью на публичный диспут по «геометрии, арифметике или связанным с ними дисциплинам, таким как астрология, музыка, космография, перспектива, архитектура и др.» Завязалась горячая дискуссия, за которой следила вся Италия. Это был первый в истории науки спор о том, надо ли сохранять научные открытия в тайне. На публичном диспуте в Милане победа осталась за Феррари. Тарталья жаловался, что не смог полностью изложить свои доводы из-за беспорядка, устроенного сторонниками Феррари.
В настоящее время большинство учёных сходится на том, что первым решение кубического уравнения нашёл дель Ферро; Фиоре узнал его от своего учителя; Тарталья переоткрыл формулу дель Ферро (такое нередко бывает в науке); Кардано же дал полную и исчерпывающую теорию решения любого уравнения третьей степени.
После конфликта с Кардано и проигрыша поединка его ученику Феррари (1548), авторитет Тартальи сильно уменьшился. Последние годы он занимался переводами Архимеда и Евклида на итальянский язык.
Учеником Тартальи был другой выдающийся учёный эпохи Возрождения – Джамбатиста Бенедетти, итальянский механик, математик, астроном, теоретик музыки, считающийся одним из предшественников Галилея в построении классической механики.
Работы Тарталья посвящены вопросам математики, механики, геодезии, баллистики, фортификации. В трактате «Новая наука» (1537) он впервые рассматривает вопрос о траектории выпущенного снаряда, причём утверждает, что траектория эта на всём её протяжении есть кривая линия. До него же учили, что траектория снаряда состоит из двух прямых, соединённых кривой линией; тут же он показывает, что наибольшая дальность полёта соответствует углу в 45°; кроме того, в этой книге рассматриваются различные вопросы об измерении поверхности полей.
Вместе с вопросами артиллерии Тарталья занимался также и вопросами укрепления городов и фортификацией вообще и в сочинении «Quesiti et invenzioni diverse» (1546) он предлагает даже особую систему фронта; он пишет также о топографической съёмке с помощью буссоли и излагает историю открытия им решения кубических уравнений. В сочинениях «La travagliata invenzione» и «Ragionamenti sopra la Travagliata invenzione» (оба 1551 года) говорится о разных изобретениях автора, которые он приписывает себе, но все они уже изложены в 1550 г. в книге Кардано «De subtilitate» и принадлежат последнему.
Тарталья перевёл на итальянский язык «Начала» Евклида – это был первый перевод этой книги на современный язык.
Публикуя свои книги «Новая наука» (1537 г.) и «Проблемы и различные изобретения» (1546 г.), Тарталья писал, что в них «. новые изобретения, не краденые ни у Платона, ни у Плотина, ни у какого иного грека или латинянина, а полученные лишь искусством, измерением и разумом». Книги написаны в форме диалогов, на итальянском языке.
Наиболее обширное сочинение автора называется «Большой трактат о числах и мерах» (1556–1560); в нём подробно рассматриваются многие вопросы арифметики, алгебры и геометрии. В частности, в работе приводится формула, иногда именуемая формулой Тарталья или Герона – Тарталья, но открытая художником Пьеро делла Франческа в XV веке, с помощью которой можно найти объём произвольного тетраэдра через шесть расстояний между его вершинами. Это трёхмерный аналог формулы Герона для площади треугольника.
Умер Н. Тарталья 13 декабря 1557 года в Венеции. Обстоятельства его смерти неизвестны.
Тарталья вместе с Кардано и его учеником Феррари проложили главную тропу на пути, по которому в дальнейшем стала развиваться алгебра.
Заслуги Н. Тартальи в геометрии скромнее. Но и они весомы: как уже отмечалось, он перевел на итальянский сочинения Евклида и Архимеда — с тем, чтобы все желающие, включая таких же бедняков, каким он был сам, могли прочесть труды блестящих древнегреческих геометров.
Геометрические предпочтения самого Тартальи близки по духу идеям арабского математика Абу-ль-Вафы (940–998), который большое внимание уделял построениям с помощью линейки и циркуля постоянного раствора.
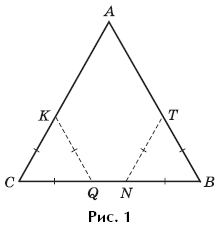
Задача Тартальи. На отрезке BC построить равносторонний треугольник ABC.
Решение. Строим равносторонние треугольники BTN и CKQ со стороной, равной данному раствору циркуля (рис. 1). Прямые BT и CK пересекутся в искомой вершине A.
Имя Тарталья носят следующие математические объекты: формулы Кардано – Тарталья; формула Герона – Тарталья.
math4school.ru
Никколо Тарталья
ок. 1499–1557
… У меня не было другого наставника, кроме спутника бедности – предприимчивости.
Никколо Тарталья (1499 – 13 декабря 1557) – итальянский математик, инженер фортификационных сооружений, геодезист, имя которого неразрывно связано с разработкой способа решения кубических уравнений в радикалах.
О жизни Тарталья известно не очень много. Хотя остались его сочинения, но очень мало сведений о его жизни. Даже точная дата рождения Никколо Тартальи неизвестна: то ли 1499, то ли 1500 или даже 1501 год. Неизвестна и его фамилия, считается, что Фонтана. Тарталья – это прозвище, от итальянского слова tartaglia – заика.
Никколо жил во времена так называемых Итальянских войн (1494-1559), которые вели между собой Франция и Испания за право владеть Италией. Родился в Брешии. Отца своего он звал по имени Micheletto (Микелетто), и занимался он тем, что переправлял грузы и почту между Брешии и близлежащими городами. Хотя семья не была богатой, отец делал всё возможное, чтобы обеспечить жену, дочь и двух сыновей. Некоторое время Никколо Тарталья даже посещал школу, но после гибели отца в 1506 году семья погрузилась в крайнюю нищету, и ни о каком образовании не могло быть и речи.
В 1512 году, во время взятия Брешии французами, когда он с матерью спасался в соборе, он получил рану в нижнюю часть лица, вследствие которой произношение его стало неправильным. Поэтому товарищи прозвали его заикой, и прозвище это сделалось его фамилией.
В возрасте 14 лет, он был отдан в обучение публичному писцу, но так как мать его не могла аккуратно платить учителю, то Тарталья должен был вновь прекратить учение.
С тех пор я учился сам, и у меня не было другого наставника, кроме спутника бедности – предприимчивости,
– пишет Тарталья в одной из своих книг. Обладая большой настойчивостью и терпением, он научился читать сам. Пристрастившись к математике, он достиг того, что сдал экзамены на звание «магистра абака» (что-то вроде учителя арифметики) и начал работать в частном коммерческом лицее и впоследствии стал известным математиком своего времени. Преподавал он в Вероне, Брешии и Венеции.
Учеником Тартальи был другой выдающийся учёный эпохи Возрождения – Джамбатиста Бенедетти, итальянский механик, математик, астроном, теоретик музыки, считающийся одним из предшественников Галилея в построении классической механики.
Во времена, кода жил Тарталья, обычным делом было проведение научных поединков и турниров, на которых ученые состязались между собой в том, кто быстрее и больше решит задач, предложенных противником. Победитель получал деньги, обретал славу, ему предлагали занять почетную, хорошо оплачиваемую должность.
В конце 1534 года Тарталья получил вызов на такое состязание от некоего Антонио Фиоре – ученика известного профессора математики Болонского университета Сципиона дель Ферро. Никколо узнал, что Фиоре владеет секретом решения кубического уравнения, который ему сообщил его учитель дель Ферро. Тарталья сел за письменный стол и за несколько дней до диспута нашел способ решения уравнения третьей степени.
Я применил все рвение, прилежание и искусство, чтобы найти правило этих уравнений, и это удалось за десять дней до срока… благодаря счастливой судьбе
– вспоминал позже Тарталья. Поединок состоялся 12 февраля 1535 года. Каждому из состязающихся надо было решить по 30 задач. За два часа Тарталья справился со всеми задачами, предложенными ему Фиоре, а тот не решил ни одной задачи противника. Победа была полной. Фиоре не мог поверить происходящему и обвинил Тарталья в краже формул, но доказать ничего не смог. К Тарталья пришли слава и почёт.
Вопрос о том, действительно ли Тарталья независимо открыл метод дель Ферро, неоднократно обсуждался. Высказывалось предположение, что на самом деле Тарталья каким-то образом получил доступ к записям дель Ферро. В качестве косвенных доказательств этой гипотезы историки ссылались на то, что других серьёзных математических достижений у Тартальи не было.
Историк науки Мориц Кантор считает, что у Тартальи было слишком мало времени для решения проблемы, над которой лучшие умы бились на протяжении двух тысячелетий. Кроме того, добавляет он, решения Тартальи и дель Ферро похожи как две капли воды.
В настоящее время большинство ученых сходится на том, что первым решение кубического уравнения нашел дель Ферро; Фиоре узнал его от своего учителя; Тарталья переоткрыл формулу дель Ферро (такое нередко бывает в науке); Кардано же дал полную и исчерпывающую теорию решения любого уравнения третьей степени.
С просьбой сообщить ему алгоритм решения алгебраического уравнения третьей степени к Тарталье обратился другой известный ученый Джироламо Кардано, который был одновременно математиком и механиком, врачом и алхимиком, хиромантом и личным астрологом римского папы.
Много раз Кардано просил Тарталью показать ему формулы, позволяющие находить корни кубического уравнения, и каждый раз получал отказ. Наконец, в 1539 году Тарталья открыл свой секрет Кардано, взяв с того слово никогда не публиковать сообщенные ему сведения. Но через шесть лет Кардано нарушил свою «священную клятву».
В 1545 году он издал труд «Великое искусство, или о правилах алгебры», где привел алгоритмы решения уравнений третьей и четвертой степени. В предисловии к книге Кардано пишет:
В наше время Сципион дель Ферро открыл формулу, согласно которой куб неизвестного плюс неизвестное равен числу. Это была очень красивая и замечательная работа. Соревнуясь с ним, Никколо Тарталья из Брешии, наш друг, будучи вызван на состязание с учеником дель Ферро по имени Антонио Марио Фиоре, решил, дабы не быть побежденным, ту же самую проблему и после долгих просьб передал ее мне.
И хотя Кардано честно написал о том, от кого он узнал секрет решения уравнения третьей степени, Тарталья был оскорблён и пребывал в гневе. У Тарталья бал тяжёлый характер. Вот что писал о нём его современник Р. Бомбелли:
Этот человек по натуре своей был так склонен говорить только дурное, что, даже хуля кого-либо, считал, что дает ему лестный отзыв.
В адрес Кардано полетели оскорбления и угрозы, тот не ответил.
В конце жизненного пути Кардано написал автобиографическую книгу «О моей жизни», в которой есть такие строчки:
Сознаюсь, что в математике кое-что, но в самом деле ничтожное количество, я заимствовал у брата Никколо.
Возможно, его все-таки мучила совесть.
За честь Кардано вступился Лодовико (Луиджи) Феррари и написал Никколо резкое письмо. В заключение он вызвал Тарталью на публичный диспут по «геометрии, арифметике или связанным с ними дисциплинам, таким как астрология, музыка, космография, перспектива, архитектура и др.»
Поединок состоялся 10 августа 1548 года в Милане. Косноязычному Тарталье было трудно противостоять молодому блестящему Феррари, и он потерпел поражение. Бесславное для Тартальи завершение диспута уронило его научный авторитет и сильно повредило дальнейшей карьере.
Феррари же приумножил свою славу. К слову, успех этот нельзя назвать случайным. С 15 лет Феррари был учеником у миланского математика Джероламо Кардано и быстро обнаружил выдающиеся способности. В восемнадцать лет Феррари стал профессором Миланского университета. А имя своё в историю математики вписал тем, что сумел найти способ для решения уравнений четвёртой степени аналогичный алгоритму решения кубических уравнений. Оба алгоритма Кардано опубликовал в своей книге «Высокое искусство».
В оставленных Тартальей сочинениях он рассматривает не только вопросы математики, но и некоторые вопросы практической механики, баллистики и топографии. Так, в первом из его сочинений, «Новая наука» (1537), он впервые рассматривает вопрос о траектории выпущенного снаряда, причём утверждает, что траектория эта на всём её протяжении есть кривая линия, между тем как до него учили, что траектория снаряда состоит из двух прямых, соединённых кривой линией; тут же он показывает, что наибольшая дальность полёта соответствует углу в 45°; кроме того, в этой книге рассматриваются различные вопросы об измерении поверхности полей.
Вместе с вопросами артиллерии Тарталья занимался также и вопросами укрепления городов и фортификацией вообще и в сочинении «Вопросы различных изобретений» (1546) он предлагает даже особую систему фронта, по начертанию схожего с тенальным; он трактует также о топографической съёмке с помощью буссоли и излагает историю открытия им решения кубических уравнений. В сочинениях «La travagliata invenzione» и «Ragionamenti sopra la Travagliata invenzione» (1551) говорится о разных изобретениях автора, которые он приписывает себе, но все они уже были изложены в 1550 году в книге Кардано и принадлежат последнему.
Наиболее обширное сочинение автора называется «Большой трактат о числах и мерах» (1556–1560); в нём подробно рассматриваются многие вопросы арифметики, алгебры и геометрии. В частности, в работе приводится формула, иногда именуемая формулой Тарталья или Герона – Тарталья, но открытая художником Пьеро делла Франческа в XV веке, с помощью которой можно найти объём произвольного тетраэдра через шесть расстояний между его вершинами. Это трёхмерный аналог формулы Герона для площади треугольника.
После поражения от Феррари Тарталья стали меньше приглашать читать лекции, и он занимал себя тем, что переводил на итальянский язык труды Архимеда и Евклида. Начал выходить его многотомный «Общий трактат о числе и мере» (1556-1560), издание которого завершилось уже после смерти учёного.
Никколо Тарталья умер 13 или 14 декабря 1557 года. Обстоятельства его смерти неизвестны.
Имя Тарталья носят следующие математические объекты:
По материалам статьи В.П. Лишевского «Затянувшийся спор. К 500-летию со дня рождения Никколо Тартальи» (Вестник Российской АН, том 70, № 2, 2000) и Википедии.