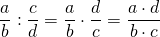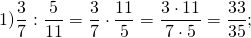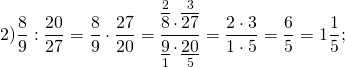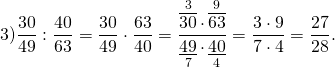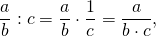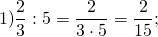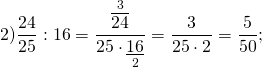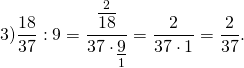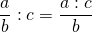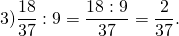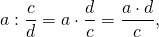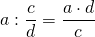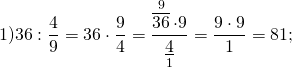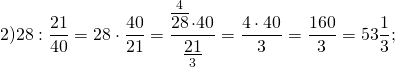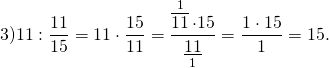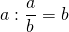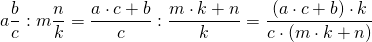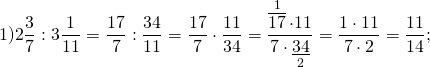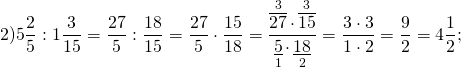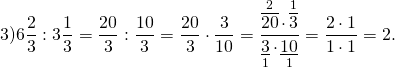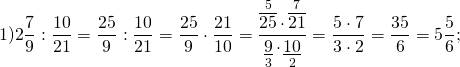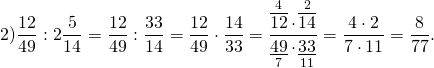Что нужно чтобы разделить дробь на дробь

Деление дробей: теория и практика

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.

Дроби бывают двух видов:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дроби

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Две дроби a/b и c/d называются равными, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Деление дробных чисел

Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.

Свойства деления:

1. При делении на единицу получится такое же число:

2. На ноль делить нельзя.

3. Когда делим ноль на любое число, всегда получаем ноль:

4. Когда делим любое число на само себя получаем единичку:

5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:

6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:

7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:

Записывайся на онлайн обучение по математике, с лучшими учителями! Для учеников с 1 по 11 классы!

Деление обыкновенных дробей

Как делить дробь на дробь? Выполняем следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.

Деление дроби на натуральное число

Для деления дроби на натуральное число нужно:

Деление натурального числа на дробь

Чтобы поделить натуральное число на обыкновенную дробь нужно:

Деление на смешанное число

Для деления смешанных чисел необходимо:

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Источник

Деление дробей. Правила. Примеры.

Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.

Деление дроби на дробь.

Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.

Деление дроби на число.

Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.

Выполните деления дроби на натуральное число \(\frac<4> <7>\div 3\).

Как мы уже знаем, что любое число можно представить в виде дроби \(3 = \frac<3> <1>\).

Деление числа на дробь.

Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.

Выполните деление числа на дробь.

Деление смешанных дробей.

Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.

Выполните деление смешанных дробей.

Деление числа на число.

Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.

Примечание к теме деление дробей:
На нуль делить нельзя.

Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.

Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.

Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) \(\frac<5> <9>\div \frac<8><13>\) б) \(2\frac<4> <5>\div 1\frac<7><8>\)

\( \frac<8><13>\) – делитель, \( \frac<13><8>\) – обратная дробь делителя.

\( \frac<15><8>\) – делитель, \( \frac<8><15>\) – обратная дробь делителя.

Пример №2:
Вычислите деление: а) \(5 \div 1\frac<1><4>\) б) \(9\frac<2> <3>\div 8\)

Источник

Деление обыкновенных дробей: правила, примеры, решения

С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.

Деление обыкновенных дробей

Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.

Отсюда получим и сформулируем правило деления обыкновенных дробей:

Запишем правило в виде выражения: a b : c d = a b · d c

Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.

Перейдем к рассмотрению деления обыкновенных дробей.

Ответ: 9 7 : 5 3 = 27 35 .

При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.

Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15 : 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9

Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9

Деление необыкновенной дроби на натуральное число

Рассмотрим данное деление дроби на число.

Решение

Ответ: 16 45 : 12 = 4 135 .

Деление натурального числа на обыкновенную дробь

Ответ: 25 : 15 28 = 46 2 3 .

Деление обыкновенной дроби на смешанное число

При делении обыкновенной дроби на смешанное число легко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.

Деление смешанного числа производится таким же образом, как и обыкновенных.

Источник

Деление дробей

Деление дробей — тема, которая включает в себя действия с обыкновенными дробями, смешанными числами и десятичными дробями.

Запишем на одной странице все правила, касающиеся деления обыкновенных дробей, смешанных чисел и натуральных чисел.

Чтобы разделить дробь на дробь, надо делимое умножить на число, обратное делителю.

(то есть первую дробь нужно переписать без изменений и умножить её на «перевёрнутую» вторую дробь).

При умножении дробей проще сокращать множители, чем результат.

Если в результате получается неправильная дробь, нужно выделить из неё целую часть.

Примеры деления обыкновенных дробей :

Применив правило деления обыкновенных дробей

Чтобы разделить дробь на натуральное число, надо знаменатель умножить на это число, а числитель оставить без изменения.

Примеры деления обыкновенной дроби на число :

Заметим, что если числитель дроби делится на число без остатка, при делении можно числитель разделить на число, а знаменатель оставить тем же:

Стоит ли запоминать ещё одно правило или использовать одно правило для всех случаев — решать вам.

Применив правило деления обыкновенных дробей

чтобы разделить натуральное число на дробь, надо в числитель записать произведения этого числа и знаменателя, а в знаменатель записать числитель.

Можно запомнить это правило и применять его в дальнейшем. А можно делить число на дробь, применяя для всех случаев деления дробей одно правило. Выбирайте, что для вас удобнее.

Примеры деления натурального числа на дробь :

Здесь можно сделать ещё один вывод:

Чтобы разделить смешанные числа (смешанные дроби), надо превратить их в неправильные дроби и разделить по правилу деления обыкновенных дробей:

(эту формулу запоминать не надо. Достаточно знать, как переводить смешанные дроби в неправильные и делить обыкновенные дроби).

Примеры деления смешанных дробей :

Примеры деления смешанного числа и обыкновенной дроби :

В следующий раз рассмотрим все правила, касающиеся деления десятичных дробей.

Источник

Урок 18 Бесплатно Деление

В прошлых уроках мы разобрали операции сложения, вычитания и умножения над дробями, а также над смешанными числами.

В этом уроке мы будем разбирать, как можно делить одну дробь на другую, как разделить дробь на натуральное число, а также поработаем с делением смешанных чисел.

Деление дроби на натуральное число

Дробь по своей сути является делением числителя на знаменатель, но записанное в таком виде, что мы это считаем это одним числом.

Если одно яблоко разделить на двоих, то каждый получит по \(\mathbf<\frac<1><2>>\) яблока.

Теперь представим, что одну половинку мы еще раз разделили на троих. Понятно, что каждая треть половинки будет представлять из себя \(\mathbf<\frac<1><6>>\) исходного яблока.

Из сказанного становится ясно, что если мы хотим поделить дробь на натуральное число, то результатом будет дробь с таким же числителем, а знаменателем будет произведение знаменателя исходной дроби и натурального числа.

Рассмотрим еще пару примеров для понимания:

Пример 1

Разделите \(\mathbf<\frac<3><7>>\) на 5

В этом примере мы просто воспользовались правилом: в знаменатель ответа записали произведение знаменателя исходной дроби и натурального числа, а числитель оставили, как у исходной дроби.

Пример 2

Разделите \(\mathbf<\frac<12><13>>\) на 6

Как мы видим, в процессе деления появляются новые возможности для сокращения дробей.

Пройти тест и получить оценку можно после входа или регистрации

Деление дроби на дробь

Мы разобрались с простым случаем деления дроби на натуральное число, теперь разберем деление дроби на другую дробь.

Здесь также можно прибегнуть к логике перед тем, как посмотреть на готовое правило.

Мы определенно хотим уменьшить первое число.

Поэтому нужно разделить имеющуюся дробь на числитель второй дроби так, как мы это делали с натуральными числами.

Но в таком случае мы уменьшим число слишком сильно, значит, нужно умножить результат ровно на столько, на сколько вторая дробь меньше значения числителя этой самой второй дроби.

Иными словами, нам нужно разделить исходную дробь на числитель второй дроби и домножить на ее знаменатель.

Если вы сейчас не до конца поняли смысл этого правила и почему оно именно такое, можете не переживать, после рассмотрения примеров и самостоятельного решения тестов понимание улучшится.

Заметим, что при делении правильной дроби на натуральное число невозможно получить неправильную дробь, так как мы уменьшаем число и так меньшее единицы.

Здесь же мы имеем деление на правильную дробь, что, по сути своей, является умножением на неправильную, то есть увеличением.

Поэтому мы можем получать в результате неправильную дробь, которую нужно будет привести в вид смешанного числа.

В этом случае у нас также получилось число, большее единицы, и мы выделяли целую часть.

Также мы можем заметить, насколько удобно в таких случаях делать сокращения до того, как посчитан результат, так как числитель и знаменатель расписаны как произведения меньших чисел.

После того как мы расписали деление, мы можем спокойно разбить одну дробь на две и получится именно то, что мы утверждали.

Пройти тест и получить оценку можно после входа или регистрации

Деление смешанных чисел

Как и для других действий, для деления смешанных чисел их можно преобразовать в неправильные дроби и пользоваться правилами для дробей.

Так, чтобы разделить смешанное число на натуральное, мы умножаем целую часть смешанного числа на его знаменатель и прибавляем это к числителю дробной части смешанного числа, а дальше умножаем знаменатель на натуральное число.

Разделим \(\mathbf<1\frac<3><4>>\) на 14:

Для деления так же, как и для сложения, работает распределительное свойство.

Другой вопрос, что, пользуясь распределительным свойствам для деления смешанного числа на натуральное, вы с высокой вероятностью получите две дроби, которые потом еще надо будет складывать, и вы потеряете на этом время.

Но иногда могут быть «красивые» случаи, когда распределительное свойство может помочь.

Например, поделим \(\mathbf<16\frac<1><9>>\) на 2

Поэтому всегда имеет смысл смотреть на числа и прикидывать, каким способом решать будет быстрее.

Другой вопрос, что решение, каким способом решать задачу, нужно принимать достаточно быстро, чтобы осталось время собственно решить задачу.

Аналогично деление смешанного числа на натуральное. Для того чтобы поделить смешанное число на дробь, его нужно представить в виде неправильной дроби.

А если числа достаточно велики, то может быть удобнее представить деление как умножение на обратное число и воспользоваться распределительным свойством умножения относительно сложения.

Рассмотрим какой-нибудь пример и решим его двумя способами.

Первый способ (с представлением смешанного числа в виде неправильной дроби):

Второй способ (применяя распределительное свойство умножения относительно сложения):

Как и ожидалось, во втором случае в процессе подсчета числа были меньше, но, как это обычно бывает в случае применения распределительного свойства умножения относительно сложения, самих действий стало больше.

Ну, и в заключение надо упомянуть про деление одного смешанного числа на другое.

Представим вторую дробь как неправильную дробь, а дальше заменим деление на неправильную дробь умножением на число, обратное ей.

Заметим, что обратное число к неправильной дроби будет меньше единицы, то есть дробью правильной.

А это значит, что сложность деления одного смешанного числа на другое смешанное отличается от умножения смешанного числа на правильную дробь исключительно взятием обратного числа от второго смешанного числа.

Также разберем один пример, используя оба способа, и сделаем выводы.

Первый способ (с представлением обоих чисел в виде неправильных дробей):

Не надо пугаться того, что в ответе в знаменателе стоит трехзначное число.

В учебниках и задачниках нередко получаются компактные ответы, но в реальных случаях экономики или физики никто не подгоняет числа, и ответы могут получаться куда более страшными.

Второй способ (применяя распределительное свойство):

В данном случае сложно сказать, какой из способов оказался удобнее. В данном примере они приблизительно одинаковы по простоте, поэтому вы можете выбирать тот способ, который удобен именно вам.

Пройти тест и получить оценку можно после входа или регистрации

Источник