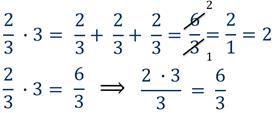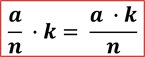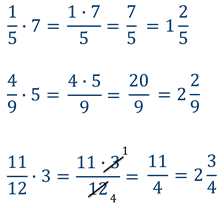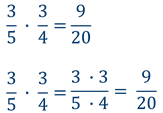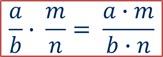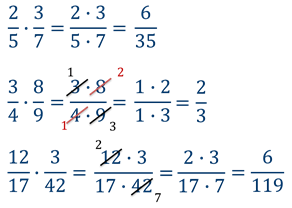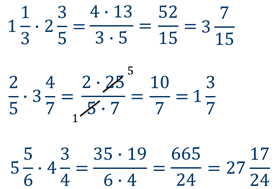Что нужно чтобы умножить дробь на дробь

Умножение дробей

Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.

Умножение обыкновенной дроби на дробь

Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей.

Чтобы умножить дробь на дробь, надо:

Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Умножение дроби на натуральное число

Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.

Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел

Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число

Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.

Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.

Источник

Умножение дробей.

Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.

Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.

Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.

Умножение дроби на число.

Воспользуемся этим правилом при умножении.

Неправильную дробь \(\frac<20> <7>= \frac<14 + 6> <7>= \frac<14> <7>+ \frac<6> <7>= 2 + \frac<6><7>= 2\frac<6><7>\\\) перевели в смешанную дробь.

Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:

Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.

Умножение взаимно обратных дробей и чисел.

Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.

Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.

Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.

Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.

Пример №1:
Вычислите произведение: а) \(\frac<8> <9>\times \frac<7><11>\) б) \(\frac<2> <15>\times \frac<10><13>\)

Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac<17><23>\) б) \(\frac<2> <3>\times 11\)

Пример №3:
Напишите число обратное дроби \(\frac<1><3>\)?
Ответ: \(\frac<3> <1>= 3\)

Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac<104> <215>\times \frac<215><104>\)

Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?

Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac<2><3>\) правильная, обратная ей дробь будет равна \(\frac<3><2>\) – неправильная дробь. Ответ: нет.

в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac<3><1>\), то обратная ей дробь будет \(\frac<1><3>\). Дробь \(\frac<1><3>\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac<1> <1>= \frac<1> <1>= 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.

Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac<4><5>\) б) \(1\frac<1> <4>\times 3\frac<2><7>\)

Решение:
а) \(4 \times 2\frac<4> <5>= \frac<4> <1>\times \frac<14> <5>= \frac<56> <5>= 11\frac<1><5>\\\\ \)
б) \(1\frac<1> <4>\times 3\frac<2> <7>= \frac<5> <4>\times \frac<23> <7>= \frac<115> <28>= 4\frac<3><7>\)

Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?

Источник

Умножение обыкновенных дробей: правила, примеры, решения

Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.

Как умножить одну обыкновенную дробь на другую

Запишем сначала основное правило:

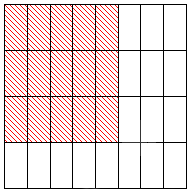
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32 ). Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.

Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:

5 8 · 3 4 = 5 · 3 8 · 4 = 15 32

Разберем решения нескольких задач на умножение обыкновенных дробей.

Решение

Все решение можно записать так:

7 11 · 9 8 = 7 · 9 11 · 8 = 63 88

Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.

Решение

Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:

4 15 · 55 6 = 4 · 55 15 · 6 = 220 90

Поясним, как это выглядит, используя данные конкретной задачи.

Решение

Запишем вычисления, исходя из правила умножения. У нас получится:

4 15 · 55 6 = 4 · 55 15 · 6

Далее мы можем просто сократить некоторые множители и получить следующее: .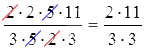

Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:

2 · 11 3 · 3 = 22 9 = 2 4 9

Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:

a b · c d = c d · a b = a · c b · d

Как перемножить обыкновенную дробь с натуральным числом

Запишем сразу основное правило, а потом попробуем объяснить его на практике.

Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:

a b · n = a b · n 1 = a · n b · 1 = a · n b

Поясним нашу мысль конкретными примерами.

Решение

2 27 · 5 = 2 · 5 27 = 10 27

Ответ: 2 27 · 5 = 10 27

Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.

Решение

Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.

Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:

a b · n = n · a b = a · n b

Как выполнить умножение трех и более обыкновенных дробей

Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.

Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.

Покажем на примере, как это делается.

Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.

1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · ( 2 · 2 · 3 ) · 3 · 5 2 · 2 · 5 · 5 · 7 ( 2 · 2 · 2 ) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280

Решение

Источник

Как умножить дробь на дробь?

Ответ или решение 2

В умножении дробей существует несколько возможных вариантов:

Умножение обыкновенных дробей

Давайте вспомним правило, что называется обыкновенной дробью.

Обыкновенные дроби – это записи вида m/n, где m и n – любые натуральные числа.

Приведем пример обыкновенной дроби: 1/2, 3/4, 1/5 и так далее.

Мы вспомнили понятие обыкновенной дроби, теперь вспомним правило умножения обыкновенных дробей.

Правило умножения обыкновенных дробей

Это одно из самых простых правил умножения дробей. Оно звучит так.

Чтобы умножить дробь на дробь, нужно проделать следующие действия:

1) 3/5 * 5/10 = (3 * 5)/(5 * 10) = 15/50, сократим полученную дробь на 5, получим:

2) 2/3 * 1/2 = (2 * 1)/(3 * 2) = 2/6, сократим дробь на 2, получим:

Перед тем как начать перемножать значения в числителе и знаменателе нужно проверить нельзя ли сократить на данном этапе умножения дробей нашу дробь. Это облегчит вычисления, которые придется выполнить при умножении.

1) 24/35 * 25/36 = (24 * 25)/(35 * 36); сократим перед умножением на 5: 25 в числителе дроби и 35 в знаменателе. А так же на 12: 24 в числителе дроби и 36 в знаменателе, получим:

(24 * 25)/(35 * 36) = (2 * 5)/(7 * 3) = 10/21.

Правила умножения дробей звучит следующим образом.

1. При умножении простой дроби на простую дробь, надо:
1) перемножить числители этих дробей и результат записать в числитель
2) перемножить их знаменатели и результат записать в знаменатель

2/5 * 3/ 4 = (2 * 3)/(5 * 4) = 6 /20 = 3/10.

2. Для умножения смешанных дробей, надо записать их в виде неправильных дробей, а затем воспользоваться правилом умножения простых дробей.

2 1/3 * 4 3/5 = 7/3 * 23/5 = (7 * 23)/ (3 * 5) = 161/15 = 10 11/15.

Источник

Умножение дробей

Урок 13. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Умножение дробей»

На этом уроке мы разберёмся, как умножают обыкновенные дроби. Выведем правила умножения обыкновенных дробей на натуральные числа, умножения обыкновенных дробей на обыкновенные дроби и умножения смешанных чисел.

Из этой записи нетрудно заметить, что числитель дроби умножили на натуральное число, а знаменатель оставили таким же.

Запишем правило умножения обыкновенных дробей на натуральное число:

Чтобы умножить дробь на натуральное число, нужно на это число умножить числитель, оставив неизменным знаменатель.

В буквенном виде это правило можно записать так:

Длина прямоугольника , а его ширина . Найдите площадь прямоугольника.

А теперь попробуем вывести правило умножения обыкновенных дробей. Смотрите, как получили числитель и знаменатель. Видно, что числитель первой дроби умножили на числитель второй дроби, аналогично и со знаменателями. Знаменатель одной дроби умножили на знаменатель второй дроби.

Следовательно, отсюда правило умножения обыкновенных дробей:

Чтобы умножить дробь на дробь, нужно отдельно перемножить их числители и их знаменатели и первый результат записать числителем, а второй знаменателем.

Или короче можно сказать так: чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель умножить на знаменатель.

В буквенном виде это правило можно записать так:

Мы научились умножать дробь на натуральное число, дробь на дробь. Осталось разобраться, как умножают смешанные числа.

Следовательно, запишем правило умножения смешанных чисел:

Чтобы перемножить смешанные дроби, нужно сначала преобразовать их в неправильные дроби, а затем выполнить умножение дробей.

Умножение дробей имеет переместительное и сочетательное свойства, а также распределительное свойство относительно сложения и вычитания.

Справедливы также свойства нуля и единицы при умножении.

Чтобы умножить дробь на натуральное число, можно на это число умножить числитель, оставив неизменным знаменатель.

Чтобы умножить дробь на дробь, нужно отдельно перемножить их числители и их знаменатели и первый результат записать числителем, а второй знаменателем.

Чтобы перемножить смешанные дроби, нужно сначала преобразовать их в неправильные дроби.

Источник