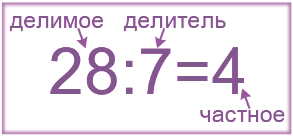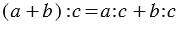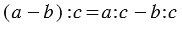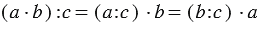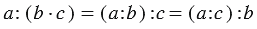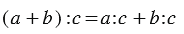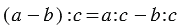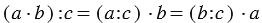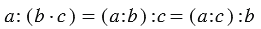Что нужно сделать чтобы найти делимое
Как найти делимое
Как найти неизвестное делимое? Поможет правило:
А что делать, если правило вдруг забылось?
В этом случае нужно придумать несложный пример на деление, с его помощью понять, что делать для нахождения делимого, и применить этот вывод, чтобы найти неизвестное делимое в своем уравнении.
Например: 10:5=2. Здесь делимое — 10. Чтобы найти 10, надо 2 умножить на 5. Точно так же поступаем при решении своего примера.
Теперь посмотрим, как найти делимое, на конкретных примерах.
| x | : | 12 | = | 60 |
| дл | дт | ч |
Чтобы найти неизвестное делимое, нужно частное умножить на делитель:
| k | : | 7 | = | 11 |
| дл | дт | ч |
Для нахождения делимого частное умножаем на делитель:
Более сложные примеры, где помимо деления есть и другие действия, мы рассмотрим позже.
Как найти делитель и неполное частное?
Итак, чтобы найти неизвестное неполное частное c нужно от делимого a отнять остаток d и полученный результат разделить на делитель b.
Решение Чтобы найти делитель, если известны делимое, неполное частное и остаток, нужно от делимого отнять остаток, и полученную разность разделить на неполное частное.
Как найти делимое делитель неполное частное остаток?
Как найти делимое, если известен делитель неполное частное и остаток Чтобы найти делимое (11) нужно неполное частное (5) умножить на делитель (2) и к полученному результату (10) прибавить остаток (1).
Что такое неполное частное 3 класс?
Неполное частное – результат деления с остатком.
Что такое неполное частное в математике?
Каким свойством обладает неполное частное?
Каким свойством обладает неполное частное при делении с остатком? Неполное частное — это наибольшее число, произведение которого на делитель меньше делимого. 2. … Остаток всегда меньше делителя.
Как найти частное и остаток при делении?
При выполнении деления с остатком полученное число называется неполным частным, а разность между делимым и произведением делителя на неполное частное называется остатком. Остаток всегда меньше делителя.
Как найти делимое и остаток?
Остаток должен быть всегда меньше делителя. Чтобы найти делимое при делении с остатком, нужно неполное частное умножить на делитель и к этому произведению прибавить остаток.
Что нужно сделать чтобы найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Как найти делимое зная делитель и остаток?
Ответ или решение 1
Откуда, делимое — это число, которое делится; делитель — число, на которое нужно делить, частное — результат деления делимого на делитель. Для того, чтоб найти делитель необходимо делимое разделить на частное.
Что такое частное чисел в математике 3 класс?
Определение частного чисел Частное чисел — это результат деления одного числа на другое. … При этом число будет делимым, а число — делителем.
Что такое неполное частное 6 класс?
Вспомните, что в частном получаем число, которое при делении с остатком, называется неполным частным. Остатком называется часть делимого, которая меньше делителя и остается в конце деления.
Что такое неполное делимое?
Если можно разделить количество единиц разряда на делитель, то это количество единиц и будет первым неполным делимым. В нашем примере это 75 тысяч. Каждая оставшаяся цифра делимого будет участвовать в формировании остальных неполных частных, о чем подробно рассказано в уроке Деление натуральных чисел.
Как определить остаток?
Как проверить деление с остатком
Чему равно делимое если делитель?
Делимое равно произведению неполного частного на делитель плюс остаток.
Деление натуральных чисел
Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.
Рассмотрим задачу:
У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?
| Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением. |
Данное действие записывают так: 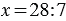
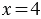
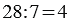
Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.
Из вышесказанного мы можем сделать вывод:
Пример: 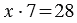
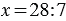
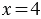
Пример: 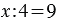
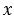
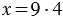
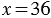
Свойства деления
Распределительные свойства:
1. Деление суммы на число:
2. Деление разности на число:
3. Деление произведения на число:
4. Деление числа на произведение:
Действия с единицей и нулем
1. Деление числа на единицу: 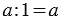
2. Деление числа на себя: 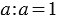
3. Деление нуля на число: 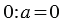
НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Свойства деления
Распределительные свойства :
1. Деление суммы на число:
а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:
б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.
Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
2. Деление разности на число:
Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?
а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:
б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:
Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.
3. Деление произведения на число:
В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?
а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:
б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:
б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.
Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.
4. Деление числа на произведение:
В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?
а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:
б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:
Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4
Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.
Действия с единицей и нулем
1. Деление числа на единицу:
У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?
Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:
2. Деление числа на себя:
Из свойств умножения мы знаем, что: 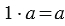
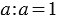
3. Деление нуля на число:
Рассуждая аналогично пункту 2 получаем: 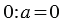
Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Это легко объяснить следующими рассуждениями: пусть мы взяли 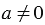
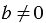
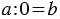
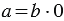
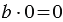
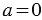
Поделись с друзьями в социальных сетях:
Нахождение неизвестных множителя, делимого или делителя
Урок 23. Математика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Нахождение неизвестных множителя, делимого или делителя»
Множитель, множитель, произведение. Делимое, делитель, частное.
Сегодня у нас непростой урок, ведь нам предстоит разобраться, как находить неизвестные: множитель, делимое или делитель. А для чего это надо уметь? Догадались? Ну конечно для того, чтобы уверенно решать уравнения! И мы, конечно же, решим несколько уравнений. Но прежде надо кое-что вспомнить.
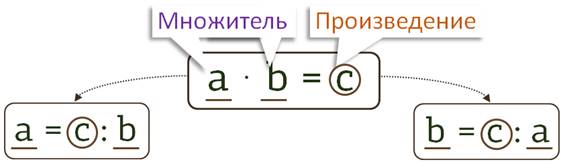
Я предлагаю вам посмотреть на буквенную запись действия умножения.
А и Б в этой записи являются множителями, Ц – произведением. Понятно, что произведение мы получаем действием умножения. Это – целое, то есть наибольшее число. А вот множители являются частями. Значит, их мы находим обратным действием, делением.
То есть, если нужно найти неизвестный множитель, мы произведение делим на известный множитель.
А теперь посмотрим на буквенную запись деления:
Обычно, целое можно разделить на части. Поэтому К, делимое, является целым, а М и Н – это части. И, естественно, что целое мы находим умножением. Поэтому, если надо найти неизвестное делимое, мы перемножаем делитель с частным.
А вот делитель является частью. И, если надо найти неизвестный делитель, то его мы найдём, разделив делимое на частное.
Ну а теперь пришло время решать уравнения. Давайте разберём вот это уравнение:
Посмотрите, это у нас осложнённое уравнение. Поэтому, прежде всего, надо его упростить, то есть, выполнить действие в правой части уравнения. Сто двадцать шесть разделить на два равно шестьдесят три. Переписываем уравнение, заменив действие деления на его результат. Здесь надо найти неизвестный множитель. Чтобы найти неизвестный множитель, мы произведение делим на известный множитель.
Шестьдесят три делим на девять, получается семь.
Не забываем выполнить проверку уравнения. Сначала переписываем его, заменив икс на его значение, которое мы получили – семь. Семью девять – шестьдесят три. Сто двадцать шесть разделить на два – шестьдесят три. Левая и правая части уравнения равны, значит, уравнение решено верно. Решаем следующее уравнение:
Неизвестное делимое находим умножением.
Ну, а следующее уравнение я предлагаю вам решить самостоятельно.
Какой компонент здесь надо найти? Неизвестный делитель. А его мы находим
Проверьте, ребята, так ли решено у вас уравнение?
Видите, как помогает при решении уравнений знание правил.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Выучите их, ребята, и не забывайте пользоваться при решении уравнений. Пока! До новых встреч!
Деление чисел
Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.
Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:
Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:
Для записи деления используется знак : (двоеточие), который ставится между числами. Например:
Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (равно), после которого записывается полученный результат:
Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?
Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.
Решение можно записать так:
Пример. Решить примеры на деление с помощью схем.
2) 12 : 4 = 3, 12: 3 = 4.
Делимое, делитель и частное
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:
12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.
Частное — это число, которое получается в результате деления. Например, в записи:
4 — это частное. При этом сама запись 12 : 3 тоже называется частным.
Проверка деления
где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:
или умножить делитель на частное: