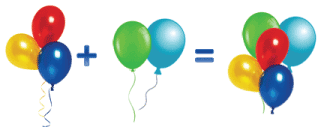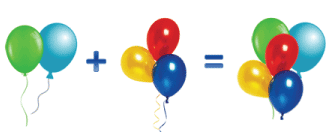Что нужно сделать чтобы найти неизвестное слагаемое
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
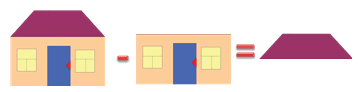
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.
Нахождение неизвестного слагаемого
Для нахождения неизвестного слагаемого надо вычесть известное из суммы.
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.
Обычно решения подобных уравнений записывают следующим образом:
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:
Нахождение неизвестного вычитаемого или уменьшаемого
Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.
Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.
Переходим к следующему правилу.
Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.
Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.
Нахождение неизвестного множителя
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Вот краткая запись всего решения:
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Для нахождения неизвестного делителя нужно разделить делимое на частное.
Последовательное применение правил
Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.
Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :
Нахождение неизвестного слагаемого, уменьшаемого, неизвестного вычитаемого
Тип урока: Урок обобщения и систематизации знаний учащихся.
Форма урока: Урок-путешествие
Ход урока
Орг. момент
1. Психологический настрой
Звонкий прозвенел звонок.
Начинается урок.
Встаньте прямо, не шумите,
Всё ль на парте, посмотрите.
Все ль на месте, всё ль в порядке:
Книжка, ручка и тетрадка.
Знает каждый ученик,
Будет нужен и дневник.
Здравствуйте, ребята. Сели.
Мы приступим к новой теме.
Ребята, вы любите путешествовать?
— Сегодня у нас необычный урок. Мы отправляемся в путешествие по Казахстану на самолете. Капитаном буду у вас я. Вас назначаю моими помощниками. А отправимся по городам Казахстана, где нас ждёт много интересного. Отправляясь в путешествие, мы возьмём с собой знания, умения, способности и дружбу. Эти качества помогут преодолеть все препятствия и достичь желаемой цели.
Мотивация:
Постарайтесь всё понять,
Ответы полные давать,
Чтоб за работу получать,
Только лишь отметку пять.
— Итак, предлагаю УСТНЫЙ СЧЁТ
Наша задача закрепить вычислительные навыки
Слайд 2 с ответами
А) уменьшите число 600 на 330 =270
Б) увеличьте число 400 на 460 = 860
В) Найдите сумму чисел 560 и 240 = 800
Г) найдите разность чисел 270 и 90 = 180
Ё) делимое – 75, делитель – 25, частное равно 3? Да, докажите 60+15=75
Найдите периметр и площадь квадрата со стороной 8 мм
Задача заполнить таблицу
| уменьшаемое | 42 | 60 | 846 | |||
| вычитаемое | 45 | 537 | 542 | |||
| разность | 36 | 85 | 28 | 362 | 140 | 834 |
— Во второй строчке – вычитаемое
— В первом столбике, что неизвестное – вычитаемое
— Как найти вычитаемое?
— Дети – Чтобы найти вычитаемое надо от уменьшаемого вычесть разность.
— Как найти уменьшаемое?
— Дети: Чтобы найти уменьшаемое надо вычитаемое сложить с разностью
Ответы 6,130,32, 899,706,1376
ВЫВОД: Так как же найти вычитаемое.
Как найти уменьшаемое.
-К то может уже догадался назвать тему нашего урока?
Дети: Находить уменьшаемое, вычитаемое
Тема урока: Нахождение неизвестного уменьшаемого, неизвестного вычитаемого
Наша задача урока: Научиться решать с неизвестными уменьшаемым и вычитаемым уравнения.
-Открываем тетради и записываем число
Проверьте свою осанку, как лежит тетрадь, поставьте ноги на пол
Ответ: 726.
Дети: мы решали уравнения, находили неизвестное уменьшаемое и вычитаемое. Научились решать уравнения с неизвестным.
Как найти слагаемое
Как найти слагаемое при решении уравнения? Это можно сделать одним из двух способов.
1) Воспользоваться правилом:
2) Если забыли правило, можно придумать простой пример на сложение.
Например, 2+5=7. Как найти первое слагаемое — 2? Надо из 7 вычесть 5. Отсюда выводим правило: чтобы найти неизвестное первое слагаемое, надо из суммы вычесть второе слагаемое.
Как найти второе слагаемое — 5? Нужно из 7 вычесть 2. Отсюда получаем: чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое.
А так как от перестановки мест слагаемых сумма не меняется, можно не уточнять, какое по счету слагаемое мы ищем.
Рассмотрим, как найти неизвестное слагаемое, на конкретных примерах.
1)
| x | + | 27 | = | 92 |
| сл. | сл. | сум. |
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:
| 43 | + | y | = | 70 |
| сл. | сл. | сум. |
Чтобы найти неизвестное слагаемое, из суммы вычитаем известное слагаемое:
Решение более сложных уравнений, содержащих несколько действий, обсудим позднее.
Нахождение неизвестного слагаемого, множителя, и т.п., правила, примеры, решения
Долгий путь наработки навыков решения уравнений начинается с решения самых первых и относительно простых уравнений. Под такими уравнениями мы подразумеваем уравнения, в левой части которых находится сумма, разность, произведение или частное двух чисел, одно из которых неизвестно, а в правой части стоит число. То есть, эти уравнения содержат неизвестное слагаемое, уменьшаемое, вычитаемое, множитель, делимое или делитель. О решении таких уравнений и пойдет речь в этой статье.
Здесь мы приведем правила, позволяющие находить неизвестное слагаемое, множитель и т.п. Причем будем сразу рассматривать применение этих правил на практике, решая характерные уравнения.
Навигация по странице.
Чтобы найти неизвестное слагаемое, надо…
Женя с Колей решили покушать яблок, для чего начали их сшибать с яблони. Женя добыл 3 яблока, а в конце процесса у мальчиков оказалось 8 яблок. Сколько яблок сшиб Коля?
Для этого существует следующее правило: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Озвученное правило позволяет по одному известному слагаемому и известной сумме определить другое неизвестное слагаемое. При этом не имеет значения, какое из слагаемых неизвестно, первое или второе. Рассмотрим его применение на примере.
Чтобы убедиться в правильности полученного ответа, желательно сделать проверку. Для этого полученный корень уравнения надо подставить в исходное уравнение и посмотреть, дает ли это верное числовое равенство.
Как найти неизвестное уменьшаемое, вычитаемое?
Связь между сложением и вычитанием чисел, про которую мы уже упоминали в предыдущем пункте, позволяет получить правило нахождения неизвестного уменьшаемого через известное вычитаемое и разность, а также правило нахождения неизвестного вычитаемого через известное уменьшаемое и разность. Будем формулировать их по очереди, и сразу приводить решение соответствующих уравнений.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Можно переходить к нахождению неизвестного вычитаемого. Оно находится с помощью сложения по следующему правилу: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
И прежде чем переходить к следующему правилу заметим, что в 6 классе рассматривается правило решения уравнений, которое позволяет выполнять перенос любого слагаемого из одной части уравнения в другую с противоположным знаком. Так вот все рассмотренные выше правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого с ним полностью согласованы.
Чтобы найти неизвестный множитель, надо…
Желательно еще сделать проверку результата: подставляем в исходное уравнение вместо буквы найденное значение, получаем 4·3=12 – верное числовое равенство, поэтому мы верно нашли значение неизвестного множителя.
И еще один момент: действуя по изученному правилу, мы фактически выполняем деление обеих частей уравнения на отличный от нуля известный множитель. В 6 классе будет сказано, что обе части уравнения можно умножать и делить на одно и то же отличное от нуля число, это не влияет на корни уравнения.
Как найти неизвестное делимое, делитель?
В рамках нашей темы осталось разобраться, как найти неизвестное делимое при известном делителе и частном, а также как найти неизвестный делитель при известном делимом и частном. Ответить на эти вопросы позволяет уже упомянутая в предыдущем пункте связь между умножением и делением.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Заметим, что разобранное правило можно трактовать как умножение обеих частей уравнения на известный делитель. Такое преобразование не влияет на корни уравнения.
Переходим к правилу нахождения неизвестного делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Проверим этот результат для надежности: 18:6=3 – верное числовое равенство, следовательно, корень уравнения найден верно.
Совместное использование правил
Последовательное применение правил нахождения неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя позволяет решать и уравнения с единственной переменной более сложного вида. Разберемся с этим на примере.
- Что нужно сделать чтобы найти неизвестное слагаемое в уравнении
- Что нужно сделать чтобы найти неизвестное уменьшаемое