Что нужно сделать чтобы найти нок

Наименьшее общее кратное: как найти

Наименьшее общее кратное — что это такое

Число, которое можно без остатка разделить на выбранные числа, является их общим кратным. Наименьшее из таких чисел — наименьшее общее кратное или сокращенно «нок».

Действия с дробями, имеющими различный знаменатель, можно значительно облегчить, если найти наименьшее общее кратное (НОК). Это такое число, например, кратное числу а, которое можно разделить на это а целиком, без остатка.

К числам, кратным 8, относятся 16, 24, 32, 40 и т.п. Кратными 9-ти являются 9, 18, 27, 36 и т.п.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Существует бесчисленное множество чисел, делящихся на а без остатка, т.е. кратных ему. В то же время, этого нельзя сказать о числе делителей. Так, делителями для 9-ти являются 9, 3, 1.

Если для двух или более натуральных чисел существует число, делящееся на оба без остатка, то оно является наименьшим общим кратным. А то из, них, которое самое маленькое, является нок.

Вычисление НОК, правила в математике

Для нахождения нок в математике существует несколько правил или алгоритмов. Самый простой вариант — вычисление НОК для двух чисел-участников. Способ легкий, но приемлем для маленьких натуральных чисел.

Нужно составить ряды чисел, кратных каждому из выбранных значений.

К (4) — 4, 8, 12, 16, 20, 24;

К (6) — 6, 12, 18, 24, 30.

Из рядов видно, что в обоих рядах встречаются числа 12 и 24. Это общие кратные. Однако 12 из них — меньшее число.

Поэтому НОК (4, 6) — 12.

Как найти НОК через НОД

Определение НОК можно провести с использованием НОД (наибольшего общего делителя).

В этом блоке изложения материала следует уточнить некоторые понятия.

Простым называется такое натуральное число, которое целиком можно разделить только само на себя либо на единицу.

Наименьшим простым числом является двойка. Она же — единственное четное натуральное простое число. Все остальные — нечетные.

Множество чисел делятся не только на 1 и на себя, но и на другие целые натуральные числа:

8 делится на 1, 2, 4, 8;

36 — на 1, 2, 3, 4, 6, 8 и т.д.

Эти числа — делители восьми и тридцати шести (делимых). Именно они могут разделить 8 и 36 без остатка. В обоих приведенных примерах делимые (8, 36) являются составными числами, поскольку имеют более двух делителей.

В приведенных рядах существуют одинаковые делители. Это 1, 2, 4, 8.

Самое большое число — 8. Оно и является наибольшим общим делителем.

Наибольший общий делитель (НОД) — число, на которое без остатка делится выбранная пара (либо больше) чисел.

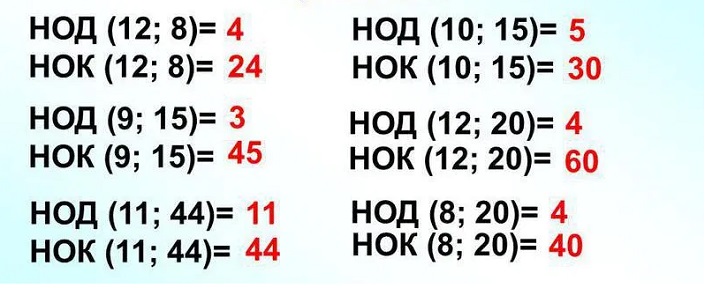
Бывают пары чисел, которые из общих делителей имеют только единицу. Тогда они называются взаимно простыми: НОД (9, 8)=1, НОД (12, 10)=1.

На следующем примере показаны пары чисел со значениями их НОД и НОК.

Решение задачи по нахождению НОК через НОД сводится к следующей формуле:

НОК чисел a,b равняется частному произведения a и b на наибольший общий делитель чисел a и b (по-другому НОД (a, b).

Исходя из этого заключения получается, что НОК и НОД взаимосвязаны друг с другом. Наименьшее общее кратное можно легко найти через наибольший общий делитель для двух или более натуральных чисел.

Как найти НОК через разложение чисел

Кроме составления рядов значений, кратных каждому из двух выбранных натуральных чисел, для правильного определения НОК пользуются методом разложения на множители.

Найденные простые множители первого разложения сравниваются с аналогичными из второго разложения, после чего они перемножаются.

После разложения числа 9 на простые множители получается ряд:

После разложения 12-ти получается ряд:

После разложения на множители числа 9 получаем: 3*3. После разложения на множители 12-ти получаем: 2*2*3. Объединяя множители обеих вариантов, получаем произведение: 3*3*2*2=36.

Наименьшее общее кратное чисел 9 и 12 — 36.

В качестве проверки произведем действия:

На практике записывают: НОК (9, 12)=36.

Такими действиями можно найти НОК более сложных чисел.

Найти НОК чисел 50 и 180.

Число 50 делится на 1, 2, 5, 10, 25, 50.

Число 180 на: 1, 5, 15, 30, 45, 90, 180.

Разложив на множители 50, получаем: 2, 5, 5.

Разложив 180, получаем: 2, 2, 3, 3, 5.

Из первого разложения выписываем: 2*5*5. Сравнивая со вторым разложением, описываем одну двойку и две тройки. После перемножения полученного ряда получается произведение: 2*5*5*2*3*3=900. Это и есть наименьшее общее кратное чисел 50 и 180.

Следовательно, НОК (50, 180)=900.

Существует еще один быстрый способ находить НОК. Он приемлем для вариантов, когда одно число нацело делится на другое. Например: НОК (15, 30)=30, НОК (20, 80)=80, НОК (16, 48)=48.

Для случаев, когда у двух чисел не имеется общих делителей, их можно просто перемножить и получить НОК. Например, НОК (7, 8)=56, НОК (4, 9)=36, НОК (7, 9)=63.

Нахождение НОК трех и большего количества чисел

Если предстоит найти НОК для большего, чем 2, количества чисел, их нужно разложить на простые множители. Например,

Сравнивая множители в каждом случае разложения натуральных чисел и выстраивая их в один ряд для умножения, получаем, что НОК (32, 40, 80) = 2*2*2*2*2*5 = 160.

В математике принято для нахождения НОК трех и более чисел применять следующую теорему:

Дано задание вычислить НОК для чисел 140 (a₁), 9 (a₂), 54 (а₃), 250 (а₄).

Для нахождения НОК (140, 9) производим действия. 140=15*9+5; 9=5*1+4.

Последующее разложение: 5=4*1+1, 4=4*1.

Следовательно, НОД (140, 9)=1. НОК (140, 9)=140*9/НОД (140, 9)=140*9/1=1260.

По аналогии вычисляем m₃ (=3780) и m₄ (=94500). Это и есть ответ решения задачи по нахождению НОК чисел 140, 9, 54, 250.

Источник

Наименьшее общее кратное (НОК): определение, примеры и свойства

Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.

Общие кратные – определение, примеры

В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.

Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.

Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.

0 является общим кратным для любого множества целых чисел, отличных от нуля.

Для всех ли чисел можно найти НОК?

Общее кратное можно найти для любых целых чисел.

Сколько всего общих кратных могут иметь данные целые числа?

Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.

Наименьшее общее кратное (НОК) – определение, обозначение и примеры

Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.

Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.

Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.

Связь между НОК и НОД

Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.

Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.

Теорема имеет два важных следствия:

Наименьшее общее кратное трех и большего количества чисел

Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.

Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:

Источник

Наименьшее общее кратное (НОК) — алгоритмы и примеры определения

trong>В школьную программу по математике входит понятие наименьшее общее кратное.Каждый ученик должен понимать и уметь находить эту величину. Это поможет проводить действия с дробями, знаменатели у которых отличаются. Вычислить этот показатель можно несколькими способами на бумаге или с помощью онлайн-калькуляторов.

Базовые понятия

Для вычисления НОК (наименьшее общее кратное) необходимо разобраться с терминами и определениями. Если любое натуральное число делится на Х без остатка, это число считается кратным Х. Например, 14, 49, 63 кратны 7.

Любое число в математике может иметь бесконечное множество кратных. А вот количество делителей для него самого ограничено. У простых чисел их всего 2 — это единица и само простое число.

НОК может быть общим сразу для нескольких величин. Если какая-то из них делится без остатка сразу на 2 числа, она называется общим кратным этой пары. Например, 10 кратно одновременно 2 и 5, то есть его можно разделить нацело на 2 и на 5. Однако для 2 и 5 кратным может быть не только 10, но и другие величины — 20, 50, 100 и так далее. С математической точки зрения, важно определить меньшую из этих величин.

Наименьшее общее кратное или НОК для величин А и В — это самое маленькое число, которое одновременно делится на А и на В. То есть оно кратно сразу А и В.

Вместо переменных можно подставлять любые числа и искать для них этот показатель.

Методы нахождения

Чтобы найти НОК 2 чисел, в математике используются три способа. Каждый из них может быть применен для проведения вычислений. Если все операции совершены правильно, в результате получится один и тот же ответ при всех методах.

Первый способ

При этом способе применяется метод простого подбора. Для многих учеников он самый простой. Порядок вычисления будет такой:

Пример: необходимо найти НОК для 6 и 8. Сначала составляется ряд кратных 6. Он будет выглядеть так: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 и так далее. Для числа 8 ряд кратных будет иметь вид: 8, 16, 24, 32, 40. 48, 56, 64, 72, 80 и так далее. Если изучить оба ряда, можно обнаружить 2 одинаковых числа — 24 и 48. Меньшим из них является 24. Это и есть НОК для 6 и 8. Для проверки делят 24 на эти величины. В обоих случаях получаются целые величины без остатка.

Второй вариант

Для вычисления вторым способом нужно разложить на простые множители обе величины. Простым множителем в математике принято называть число, которое делится без остатка только на 1 и на себя.

Следующий шаг — выписываются все множители из первого ряда. Затем добавляются те цифры, которых не было в первом ряду, но были во втором. Получится цепочка из нескольких простых чисел. Их необходимо перемножить между собой, в результате чего получится НОК.

Пример: требуется найти НОК для 8 и 12. Для начала нужно разложить на простые множители 8. Получится 2, 2 и 2. Дальше раскладывается аналогичным образом число 12. Получается 2, 2 и 3. Выписываются множители из первого разложенного ряда 2х2х2. Далее добавляются цифры из второго ряда, которых нет в первом — 2х2х2х3.

После перемножения этих величин получается 24. Это и будет НОК для 12 и 8, поскольку оно делится нацело на оба числа. Фактически все действие сводится к разложению на простые множители двух величин одновременно.

Третий алгоритм

Существует еще один метод нахождения НОК. Решать примеры с его помощью можно только для двух чисел. Необходимо заранее знать наибольший общий делитель — НОД. Так принято называть самое большое число, на которое 2 какие-либо переменные делятся без остатка. Вместо переменных можно ввести конкретные данные. НОД возможно вычислить не только для 2, но и для большего количества величин. В математике это понятие принято записывать кратко НОД (х, у).

Пример: требуется рассчитать НОД для 90 и 117. При разложении на простые множители 90 получается ряд 2,3,3,5. Ту же операцию проводят с числом 117 — получается 3,3,13. Для вычисления НОД умножают общие для двух рядов множители — 3х3=9. Значит, НОД (90,117) = 9.

Часто получается, что наибольший общий делитель равняется одному из чисел. Так бывает, если на него можно разделить все остальные. Например, для 10, 20 и 30 наибольшим делителем будет 10.

Если в задаче необходимо найти одновременно НОД и НОК, применяют третий способ вычисления. Алгоритм работы следующий:

Пример: требуется найти НОД и НОК для чисел 115 и 175. Вначале вычисляется НОД. В этом случае он будет равняться 5. Затем 25 и 40 перемножают, получается 20125.

Полученный результат делят на 5, в итоге НОК 15 и 40 равно 4025.

Чтобы проверить достоверность результата, можно вычислить НОК первым или вторым методами.

Например, нужно найти НОК (25, 40).

Наибольшим делителем для них будет 5. Тогда (25х40):5 = 200.

Проверка вторым способом:

Такой же результат будет получен и при решении вторым методом.

Особые случаи

Не во всех случаях вычисление проводится стандартными способами. Существуют пары чисел с особыми свойствами, для которых найти НОК можно без громоздких вычислений.

К таким случаям относятся следующие:

Большинство учащихся быстро усваивают, как найти НОК двух чисел.

Однако некоторых вводят в растерянность ситуации, когда требуется вычислить НОК или НОД для трех или более исходных. В этом случае необходимо последовательно находить кратное для каждой пары из имеющегося ряда.

Для этих случаев в математике есть особая теорема. Если имеется числовой ряд с формулой А1, А2, А3… Ах, то НОК для всех показателей вычисляется последовательно. Вначале НОК (А1, А2), затем для А2, А3 и так далее.

Однако такой путь может оказаться довольно трудоемким.

Чтобы сэкономить время, можно воспользоваться другим методом поиска:

Применение онлайн-калькулятора

Современные технологии позволяют не рассчитывать нужные данные на бумаге. Любой пользователь может найти в интернете НОД и НОК калькулятор, работающий в онлайн-режиме. Такой онлайн-сервис особенно удобен, если нужно найти делитель и кратное для 3 и более чисел.

Чтобы получить нужные расчеты, достаточно ввести в окошки калькулятора исходные данные и выбрать НОД или НОК. Поскольку между этими понятиями существует тесная связь, обычно они вычисляются вместе. Внизу находится кнопка «найти», которую нужно нажать. Через 2−3 секунды внизу появится ответ. Кроме того, некоторые сервисы выдают не только конечные результаты, но и пошаговый порядок расчетов. Здесь же можно найти онлайн-тесты на заданную тему.

Таким образом, учащийся может понять алгоритм действий и усвоить правило при вычислении НОК онлайн. Это всегда проще сделать на практическом примере.

Источник

Алгоритм нахождения НОД и НОК натуральных чисел

Правило нахождения наибольшего общего делителя (НОД).

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

3) найти произведение оставшихся множителей.

Пример. Найдем НОД (48;36). Воспользуемся правилом.

1. Разложим числа 48 и 36 на простые множители.

2. Из множителей, входящих в разложение числа 48 вычеркнем те, которые не входят в разложение числа 36.

Остаются множители 2, 2 и 3.

3. Перемножим оставшиеся множители и получим 12. Это число и является наибольшим общим делителем чисел 48 и 36.

НОД (48;36) = 2 · 2 · 3 = 12.

Правило нахождения наименьшего общего кратного (НОК).

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Пример. Найдем НОК (75;60). Воспользуемся правилом.

1. Разложим числа 75 и 60 на простые множители.

2. Выпишем множители, входящие в разложение числа 75: 3, 5, 5.

3. Добавим к ним недостающие множители из разложения числа 60, т.е. 2, 2.

4. Найдем произведение получившихся множителей

Правило нахождения наибольшего общего делителя (НОД).

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

3) найти произведение оставшихся множителей.

Пример. Найдем НОД (48;36). Воспользуемся правилом.

1. Разложим числа 48 и 36 на простые множители.

2. Из множителей, входящих в разложение числа 48 вычеркнем те, которые не входят в разложение числа 36.

Остаются множители 2, 2 и 3.

3. Перемножим оставшиеся множители и получим 12. Это число и является наибольшим общим делителем чисел 48 и 36.

НОД (48;36) = 2 · 2 · 3 = 12.

Правило нахождения наименьшего общего кратного (НОК).

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Пример. Найдем НОК (75;60). Воспользуемся правилом.

1. Разложим числа 75 и 60 на простые множители.

2. Выпишем множители, входящие в разложение числа 75: 3, 5, 5.

3. Добавим к ним недостающие множители из разложения числа 60, т.е. 2, 2.

4. Найдем произведение получившихся множителей

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1310284

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Для школьников к 1 сентября разработают короткие экскурсионные маршруты

Время чтения: 1 минута

Учителя Кубани смогут получить миллион рублей на взнос по ипотеке

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Новые аккредитационные показатели для вузов вступят в силу с 1 марта

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В России планируют создавать пространства для подростков

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.

Калькулятор для нахождения НОД и НОК

Как пользоваться калькулятором

Как вводить числа

Что такое НОД и НОК?

Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД.
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК.

Как проверить, что число делится на другое число без остатка?

Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.

Некоторые признаки делимости чисел

2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.

4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.

Как найти НОД и НОК двух чисел

Как найти НОД двух чисел

Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.

Рассмотрим этот способ на примере нахождения НОД(28, 36) :

Как найти НОК двух чисел

Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.

Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:

Нахождение НОД и НОК для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c).

Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)

Пример: найти НОД и НОК для чисел 12, 32 и 36.

Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.

Источник