Что нужно сделать чтобы найти уменьшаемое
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
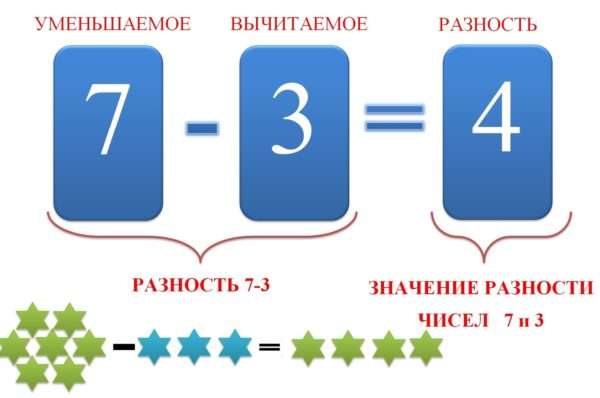
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
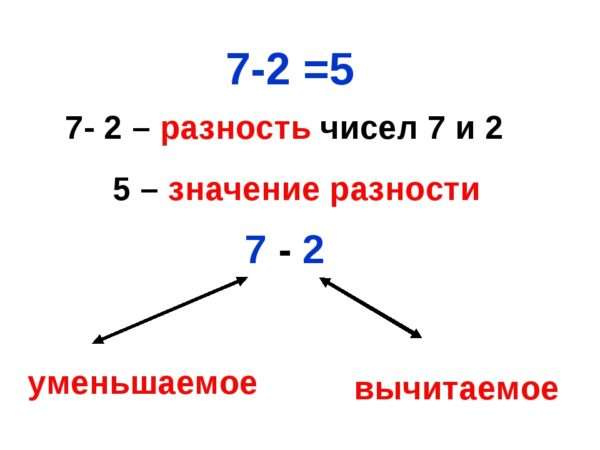
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Поиск вычитаемого, уменьшаемого и разности для первоклассников
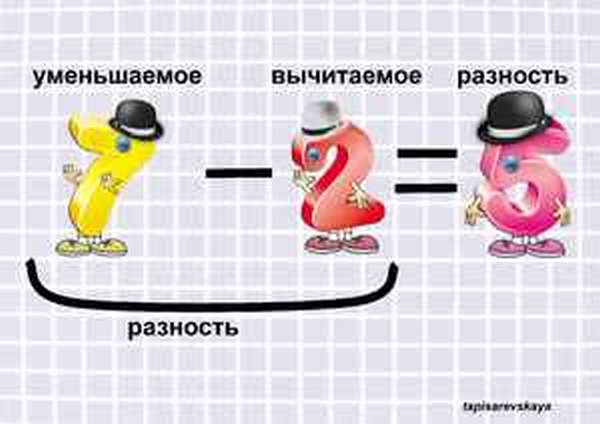
Теперь рассмотрим правила вычисления каждого из этих компонентов на простых примерах.
Чтобы сделать юным математикам понимание азов науки проще и доступнее, представим эти сложные и пугающие термины именами чисел в уравнении. Ведь у каждого человека есть имя, по которому к нему обращаются, чтобы о чем-то спросить, что-то рассказать, обменяться информацией. Учитель в классе, вызывая ученика к доске, смотрит на него и называет по имени. Так и мы, глядя на числа в уравнении, можем очень легко понять, какое число как зовут. А после уже и обратиться к числу, чтобы правильно решить уравнение или даже найти потерявшееся число, об этом чуть позже.
Это интересно: разрядные слагаемые что это?
Но, ничего не зная о числах в уравнении, давайте сначала с ними познакомимся. Для этого приведем пример: уравнение 5−3= 2. Первое и самое большое число 5 после того, как мы от него отняли 3, становится меньше, уменьшается. Поэтому в мире математики его так и называют — Уменьшаемое. Второе число 3, которое мы отнимаем от первого, тоже легко узнать и запомнить — оно Вычитаемое. Глядя на третье число 2, мы видим разницу между Уменьшаемым и Вычитаемым — это Разность, то, что мы получили в результате вычитания. Вот так.
Как найти неизвестные

Но бывают случаи, когда какое-то из чисел теряется или просто неизвестно. Что же делать? Все очень просто — для того, чтобы такое число найти, нам нужно знать только два других значения, а также несколько правил математики, и, конечно, уметь ими пользоваться. Начнём с самой лёгкой ситуации, когда нам нужно найти Разность.
Это интересно: что такое хорда окружности в геометрии, определение и свойства.
Как найти разность
Представим, что мы купили 7 яблок, подарили 3 яблока своей сестре и оставили какое-то количество себе. Уменьшаемое — это наши 7 яблок, число которых уменьшилось. Вычитаемое — это те 3 подаренных нами яблока. Разность — это количество оставшихся яблок. Что сделать, чтобы узнать это количество? Решить уравнение 7−3= 4. Таким образом, хотя мы и подарили 3 яблока сестре, у нас ещё осталось 4.
Правило поиска уменьшаемого
Теперь узнаем, что делать, если потерялось Уменьшаемое.
Как найти вычитаемое
На всякий случай можно проверить наши успехи и подставить отыскавшееся Вычитаемое в исходный пример. 7−3= 4. Разность не изменилась, а значит мы сделали все правильно. Было 7 яблок, съели 3, осталось 4.
Ну вот, теперь мы познакомились с вычитанием, его главными участниками.
Мы умеем отличать их друг от друга, находить, если они неизвестны и решать любые уравнения с их участием. Пусть эти знания помогут и пригодятся вам в начале интересного и увлекательного пути в страну Математики. Удачи!
Математика. 1 класс
Конспект урока
Математика, 1 класс
Урок № 35. Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей
Перечень вопросов, рассматриваемых в теме:
Вычитание – действие обратное сложению.
Уменьшаемое – число, из которого вычитают.
Вычитаемое – число, которое вычитают.
Разность – результат вычитания.
Слагаемое – число, которое складывают.
Сумма – результат сложения.
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Давайте решим задачу. В гараже стояли 5 машин. 2 машины уехали. Сколько машин осталось в гараже?
Для решения задачи выберем действие вычитание. Так как машины уехали, их стало меньше.
Ответ: 3 машины в гараже.
Как называются числа при вычитании?
Первое число 8 – число, из которого вычитают. Это уменьшаемое.
Второе число 5 – число, которое вычитают. Это вычитаемое.
Третье число 3 – результат вычитания. Это разность.
Выражение 8 – 5 тоже называется разность.
Равенство 8 – 5 = 3 можно прочитать так. Уменьшаемое – 8, вычитаемое – 5. Разность – 3. Или, разность восьми и пяти равна трем.
Назовем числа при вычитании.
6 – уменьшаемое, 2 – вычитаемое, 4 – разность. Выражение 6 – 2 тоже разность.
Соединим предложение с математической записью.
Уменьшаемое – 9, вычитаемое – 6. 8 – 3
Вычитаемое – 3, уменьшаемое – 8. 7 – 2
Разность чисел 7 и 2. 9 – 6
В коробке было 10 карандашей. Взяли 4 карандаша. Сколько карандашей осталось в коробке.
Для решения задачи выберем действие вычитание. Запишем разность чисел.
Ответ: 6 карандашей.
Ответим на вопросы, поставленные в начале урока.
Числа при вычитании называются уменьшаемое, вычитаемое, разность.
Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Выражение на вычитание можно читать по-разному. Например, 8 – 1 = 7
Уменьшаемое – 8, вычитаемое – 1, разность – 7. Или, разность чисел 8 и 1 равна 7.
Выполним несколько тренировочных заданий.
а) Вычитаемое – 3. Уменьшаемое – 5.
б) Разность чисел 7 и 2.
в) Сумма чисел 5 и 4.
Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.
Нахождение неизвестного слагаемого
Для нахождения неизвестного слагаемого надо вычесть известное из суммы.
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.
Обычно решения подобных уравнений записывают следующим образом:
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:
Нахождение неизвестного вычитаемого или уменьшаемого
Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.
Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.
Переходим к следующему правилу.
Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.
Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.
Нахождение неизвестного множителя
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Вот краткая запись всего решения:
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Для нахождения неизвестного делителя нужно разделить делимое на частное.
Последовательное применение правил
Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.
Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :
Неизвестное уменьшаемое
Как найти неизвестное уменьшаемое? Вариантов — два. Лучший — применить правило:
Что делать, если правило не вспоминается? Выход есть.
Надо придумать легкий пример на вычитание, и с его помощью понять, как искать неизвестное уменьшаемое.
Например: 8-3=5. 8 — уменьшаемое. Чтобы получить 8, нужно к 3 прибавить 5. Точно так же находим и неизвестное уменьшаемое в своем уравнении.
Примеры на нахождение неизвестного уменьшаемого:
| x | — | 34 | = | 58 |
| ум. | в. | р. |
Чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность:
| z | — | 351 | = | 503 |
| ум. | в. | р. |
Для нахождения неизвестного уменьшаемого к вычитаемому прибавим разность:
Позже мы рассмотрим решение более сложных уравнений.