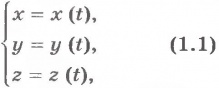Что нужно сделать чтобы описать движение материальной точки

Что нужно сделать чтобы описать движение материальной точки

Какими величинами можно описать механическое движение тела?

Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчёта.

Существует несколько способов описания, или, что одно и то же, задания движения точки. Рассмотрим два из них, которые наиболее часто применяются.

Координатный способ.

Будем задавать положение точки с помощью координат. Если точка движется, то её координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.

Математически это принято записывать в виде

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме.

Если уравнения движения известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и её положение относительно выбранного тела отсчёта. Вид уравнений для каждого конкретного движения будет вполне определённым.

Основной задачей кинематики является определение уравнения движения тел.

Количество выбираемых для описания движения координат зависит от условий задачи. Если движение точки происходит вдоль прямой, то достаточно одной координаты и, следовательно, одного уравнения, например, x(t). Если движение происходит на плоскости, то его можно описать двумя уравнениями — x(t) и y(t). Уравнения описывают движение точки в пространстве.

Векторный способ.

Положение точки можно задать, и с помощью радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, определяющий её положение, с течением времени изменяется (поворачивается и меняет длину), т. е. является функцией времени:

= (t)

На рисунке радиус-вектор определяет положение точки в момент времени t₁, а радиус-вектор ₂ — в момент времени t₂.

Вышеприведенная формула и есть уравнение движения точки, записанное в векторной форме.

Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.

Задание трёх скалярных уравнений равносильно заданию одного векторного уравнения.

Итак, мы знаем, что положение точки в пространстве определяется её координатами или её радиус-вектором.

Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?

Изобразим ось ОХ. Опустим из начала А и конца В вектора перпендикуляры на ось ОХ. Точки А₁ и В₁ есть проекции соответственно начала и конца вектора на эту ось.

Проекция вектора

Проекцией вектора на какую-либо ось называется длина отрезка А₁В₁ между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «—».

Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, а_х и а_у — проекции вектора на оси координат ОХ и OY.

Согласно определению проекции вектора на ось можно записать:

Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.

Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций.
В противном случае она считается отрицательной.

Проекция вектора на ось будет положительной, когда вектор составляет острый угол φ с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекции тупой угол φ.

Иногда нужно находить составляющие вектора, например векторы _x, и _y.

Сумма составляющих равна вектору :

= _x + _y.

Источник

Что нужно сделать чтобы описать движение материальной точки

В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.

1. Векторный способ.

В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.

Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.

В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.

Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.

Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.

Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_»cp»` тела за время `Delta t`:

`vecv_»cp»=(Deltavecr)/(Delta t)` (1)

Вектор `vecv_»cp»` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.

Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.

Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:

Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.

В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).

Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.

Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:

При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!

Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (`»м»//»с»`) и метр на секунду в квадрате ( `»м»//»с»^2`).

2. Координатный способ.

3. Естественный (или траекторный) способ.

Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.

Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.

Средней путевой скоростью `v_»cp»` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:

`v_»cp»=(Delta S)/(Delta t)` (3)

Определённая ранее средняя скорость `v_»cp»` (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.

Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_»cp»` и средняя путевая скорость `v_»cp»` троллейбуса?

Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_»ср»=Deltavecr//Deltat=0` и `|vecv_»ср»|=0`. Но средняя путевая скорость троллейбуса не равна нулю:

`v_»cp»=(Delta S)/(Delta t)=(72 «км»)/(8 «ч»)=9 «км»//»ч»`.

Источник

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения

Теоретическая механика как наука. Три основных раздела ТМ. Кинематика. Основные задачи кинематики.

Теоретическая механика – наука об общих законах механических взаимодействий между материальными телами, а также об общих законах движения тел по отношению друг к другу.

Теоретическая механика, преподаваемая в техническом вузе, содержит три раздела: кинематику, статику и динамику:

Кинематика – часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.

Статика – это учение о равновесии совокупности тел некоторой системы отсчета.

Динамика – часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

Основная задача кинематики заключается в установлении (при помощи тех или иных математических методов) способов задания движения точек или тел и в определении по уравнениям их движений соответствующих кинематических характеристик движения, таких, как траектории, скорости и ускорения движущихся точек, угловые скорости и угловые ускорения вращающихся тел и др.

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения.

Естественный способ. Этим способом пользуются, если из­вестна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве.

Математически это принято записывать в виде:

Векторный способ. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется, т. е. является функцией времени: r=r(t) (стрелочки над ними нужны). Одна такая функция равняется трем функциям (1.1). Если ввести единичные векторы i, j, k ( i = j = k = 1), направленные соответственно вдоль осей x, y и z то, очевидно, закон движения может быть представлен в виде:

Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.

Источник

Что нужно сделать чтобы описать движение материальной точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Видеоурок по физике «Способы описания движения. Траектория. Путь. Перемещение»

В этом видеоуроке мы с вами познакомимся с основными способами описания механического движения. Вспомним, какие существуют виды механического движения в зависимости от формы траектории. А также узнаем, что такое перемещение и чем оно отличается от пройдённого пути.

В начале урока напомним учащимся о том, что такое механическое движение. Механическим движением называется изменение положения тела или частей тела в пространстве относительно других тел с течением времени.

Для описания движения реального тела пользуются его моделью — материальной точкой, то есть телом, размерами и формой которого в данных условиях можно пренебречь.

Далее мы вводим два способа описания движения материальной точки: координатный и векторный.

При рассмотрении координатного способа описания движения следует обратить внимание учащихся на то, что при движении точки в выбранной системе отсчёта её координаты с течением времени изменяются. То есть они зависят от времени или, говорят, являются функциями времени.

Если уравнения движения известны, то мы можем рассчитать координаты точки для любого момента времени, а следовательно, и её положение относительно выбранного тела отсчёта.

Второй способ описания движения — векторный. В нём положение точки задаётся при помощи радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, как и координаты, является функцией времени, так как он изменяет свою длину и поворачивается.

Далее мы вводим понятие проекции вектора на ось и рассказываем, каким образом она определяется для различных случаев.

Также положение точки через некоторый промежуток времени можно определить, зная траекторию её движения, начальное положение точки на этой траектории и путь, пройденный точкой за этот промежуток времени. Далее мы напоминаем учащимся, что такое траектория движения, путь, и вводим понятие перемещения.

Здесь важно обратить внимание учащихся на то, что путь, пройденный телом, нельзя сравнивать с его перемещением, поскольку путь — величина скалярная, а перемещение — векторная.

В конце урока проводим краткое повторение изученного материала.

Источник