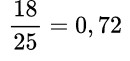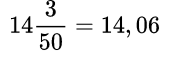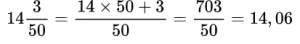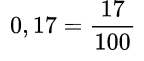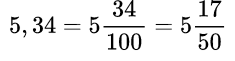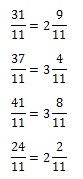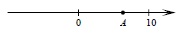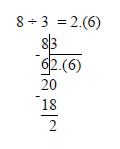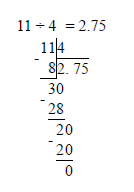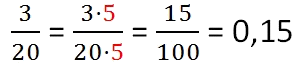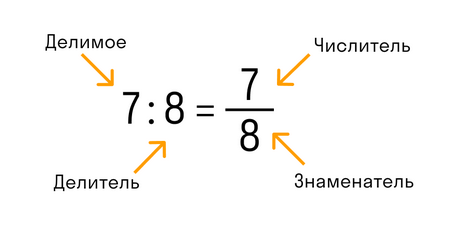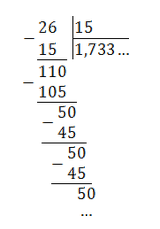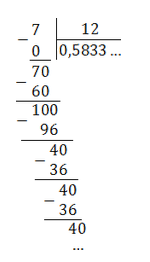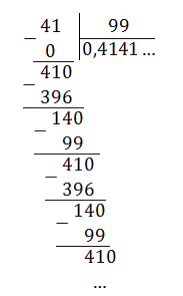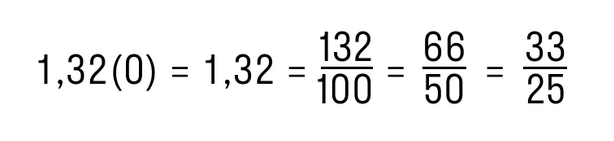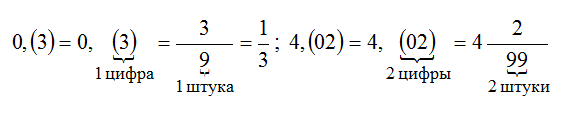Что нужно сделать чтобы перевести десятичную дробь в обыкновенную дробь
Перевод обыкновенной дроби в десятичную и наоборот
теория по математике 📈 числа и вычисления
При решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует.
Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель. Как перевести обыкновенную дробь в конечную десятичную дробь?
Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в столбик).
Пример №1. ½ = 0,5 так как 1:2=0,5
Пример №2. ¾ = 0,75 так как 3:4=0,75
Пример №3. Так как 18:25=0,72, то
Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет.
Пример №4.
здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06.
Пример №5.
в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель — это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06.
Как перевести десятичную дробь (конечную) в обыкновенную?
Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь.
Пример №6.
целая часть равна нулю, нуль перед обыкновенной дробью не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля.
Пример №7.
целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь
Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А.
pазбирался: Даниил Романович | обсудить разбор | оценить
Одно из чисел 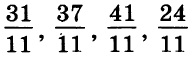
Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.
Итак, выделяем целые части:
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
pазбирался: Даниил Романович | обсудить разбор | оценить
На координатной прямой отмечена точка А:
Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?
Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.
Оцениваем 181/16 — можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Оцениваем √37 — самое близкое значение, из которого вычисляется квадратный корень — это 36, значит √37 — это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.
Посмотрим на вариант 0,6 — это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.
Вариант с ответом 4 также не подойдет по вышеуказанной причине.
pазбирался: Даниил Романович | обсудить разбор | оценить
В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.
pазбирался: Даниил Романович | обсудить разбор | оценить
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Дроби. Перевод дробей в десятичные.
Перевод дробей в десятичные производят несколькими способами.
В десятичную дробь переводят обыкновенные дроби, у которых в знаменателе после сокращения нет простых множителей (кроме 2 и 5). Когда в знаменателе несократимой обыкновенной дроби есть хотя бы 1 простой множитель, которые не равен 2 или 5, то при переводе этой дроби в десятичную получаем бесконечную десятичную дробь.
Первый способ перевода обыкновенной дроби в десятичную.
Чтобы перевести дробь в десятичную, необходимо числитель и знаменатель домножить на 1-но и то же число, таким образом, чтобы в знаменателе получили 10, 100, 1000 и так далее.
Проверяем, можно ли дробь привести к виду конечной десятичной.
Далее нужно умножить числитель и знаменатель на пять. В знаменателе получаем сто.
Второй способ перевода обыкновенной дроби в десятичную.
Этот способ сложнее, но применяется чаще.
Чтобы перевести обыкновенную дробь в десятичную, необходимо числитель дроби поделить на знаменатель этой дроби.
Проверяем, можно ли дробь привести к виду конечной десятичной.
Делим столбиком числитель на знаменатель.
Ниже приведен список дробей со знаменателями, чаще других встречающихся в задачах. Лучше их запомнить.
Как перевести десятичную дробь в обыкновенную — правило с примерами
Преобразование десятичных дробей в обыкновенные – навык нужный: в жизни нам приходится “переводить” проценты – в рубли, пропорции кулинарных рецептов – в граммы и миллилитры. Но прежде чем познакомиться с парой полезных алгоритмов по “превращению дробей”, вспомним, как сокращаются простые дроби. Нам это пригодится.
Как сокращать дроби
Сократить дробь – значит разделить числитель и знаменатель на одно и то же (максимально возможное!) число. Иногда это число очевидно, иногда – нет.
Например: в дроби оба числа делятся на 5.
Разделим: 5 : 5 = 1, 10 : 5 = 2, следовательно: = ( frac<1> <2>) .
( frac<15> <50>) = ( frac<3> <10>) (разделили все на 5)
( frac<45> <81>) = ( frac<5> <9>) (сократили на 9)
Можно эту процедуру провести в несколько шагов: ( frac<24> <108>) = ( frac<8> <36>) = ( frac<2> <9>) (сначала на 3, потом на 4, а всего на 12).
Важно! Делить числитель и знаменатель надо до тех пор, пока общие делители не закончатся, то есть пока дробь не станет несократимой.
В нашем случае знаменатель всегда будет кратен 10-и: 10, 100, 1000, 10000 и так далее. Значит, общие делители для обоих “этажей” будут те, на которые делятся эти круглые числа: 2, 4, чаще всего – 5, ну и 8, 10, 20, 25, 50 и далее. Если сразу не отыщете нужное, набирайте их постепенно.
Например: как сократить дробь ( frac<750> <1000>) ?
Итого: ( frac<750> <1000>) = ( frac<75> <100>) = ( frac<15> <20>) = ( frac<3> <4>) . Можно было сразу сократить на 250 (10 × 5 × 5 = 250).
Вот теперь можно переходить к главному.
Как превратить десятичную дробь в обычную?
Десятичные дроби (ДД) записываются в строчку: целая часть – до запятой, дробная – после запятой. Например, 3,45 или 0,299.
Обыкновенные (ОД) пишут “в два этажа”: вверху – числитель, внизу – знаменатель. Целую часть – перед дробью. Например: ( frac<4> <5>) , ( frac<25> <70>) , 3 ( frac<2> <7>) .
Есть два основных пути перевода десятичной дроби в обычную и их варианты.
Первый способ – механический
Попробуем 0,05 превратить в ( frac<1> <20>) :
Результат решения: 0,05 = ( frac<5> <100>) = ( frac<1> <20>) .
ДД с целой частью, например 3,075, преобразуем так:
Ход преобразований: 3,075 = ( frac<3075> <1000>) = ( frac<123> <40>) = 3 ( frac<3> <40>) .
Вся последовательность: 3,075 → 0,075 = ( frac<75> <1000>) = ( frac<3> <40>) → 3 ( frac<3> <40>) .
Второй способ – “на слух”
Этот подход более естественный. Каждый легко запишет под диктовку:
Также можно выразить и десятичную дробь, например, 0,45:
В итоге получаем: 0,45 = ( frac<45> <100>) = ( frac<9> <20>) .
Целое, если оно есть, можно “отложить на потом” и вернуть в конце вычислений.
Пусть требуется выразить 14,408 в виде ОД:
Ход решения: 14, 408 = 14 ( frac<408> <1000>) = 14 ( frac<51> <125>) .
Еще несколько примеров:
Самое трудное (для тех, кому не все равно)
Что делать, если нужно преобразовать периодическую десятичную дробь? Не вдаваясь в дремучие подробности, познакомимся с надежным алгоритмом.
Итак, требуется выразить 1,(6) в виде ОД.
Пусть обычная дробь – это x, который должен получиться из 1,(6).
x = 1,(6) — умножим обе части равенства на 10
10 x = 16,(6) — вычтем из обеих частей x (или 1,(6) – ведь это одно и то же)
Таким образом, 1,(6) = ( frac<15> <9>) .
Попробуйте разделить 15 на 9, и убедитесь, что получится 1,66666 – и так до бесконечности.
Если усложнить: 0,1(23) нужно представить в виде ( frac ) .
x = 0,1(23) — умножим обе части равенства на 1000
1000 x = 123,(23) — вычтем из обеих частей 10 x, другими словами, 1,(23)
Значит — 0,1(23) = ( frac<61> <495>) .
Важно! В этом примере пришлось умножить части уравнения не на 10, а на 1000, вычесть не х, а 10х. Это нужно для того, чтобы легче было искать разность периодов: из 123,(23) удобно вычитать 1,(23). Подходящие коэффициенты придется подбирать в каждом отдельном случае. Но общий ход решения остается постоянным.
Конечно, для проведения подобных вычислений можно обратиться к онлайн-калькулятору. Но, согласитесь, иметь в арсенале знаний оригинальный эффектный прием – особое удовольствие.
Еще больше примеров для полного понимания этой темы смотрите в предложенном видео.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
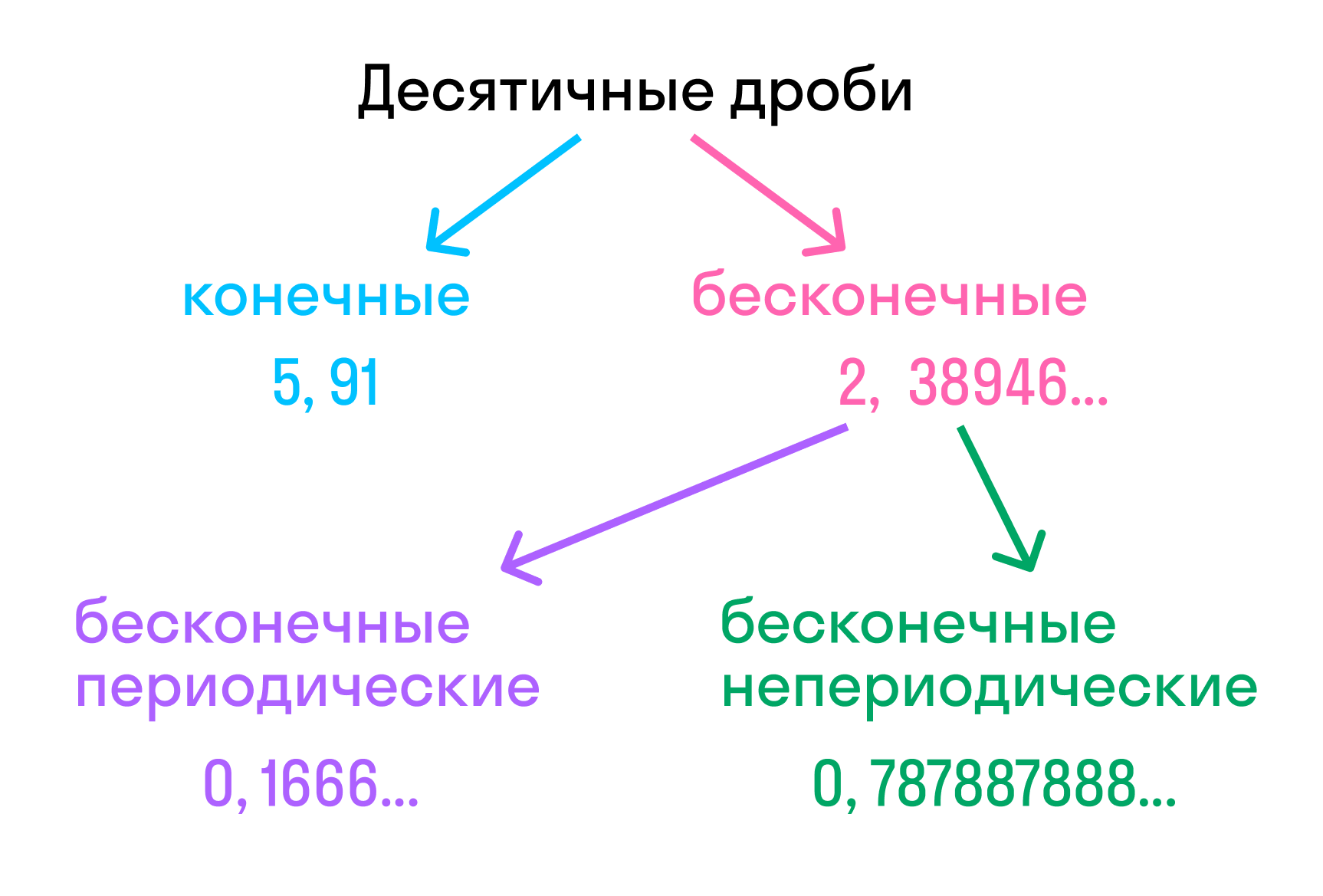
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Как перевести периодическую дробь
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Тут есть два варианта:
Чтобы задать периодическую десятичную дробь, нужно найти ее периодическую и непериодическую часть. Чтобы это сделать нужно привести дробь в неправильную, а затем разделить числитель на знаменатель столбиком.
Что будет происходить в процессе:
Повторяющиеся цифры после десятичной точки нужно обозначить периодической частью, а то, что стоит спереди — непериодической.
Пример. Перевести обыкновенные дроби в периодические десятичные:
Все дроби без целой части, поэтому просто делим числитель на знаменатель уголком:
Определение периодической дроби
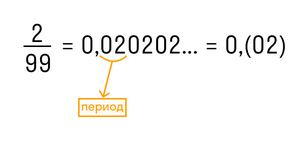
Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.
Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Виды периодических дробей: чистые и смешанные.
Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).
Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.
Рассмотрим примеры дробей, чтобы научиться определять части и период.
Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Читаем так: ноль целых три в периоде.
7/12 = 0,583333. = 0,58(3)
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.
17/11 = 1,545454. = 1,(54)
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Читаем так: одна целая пятьдесят четыре сотых в периоде.
25/39 = 0,641025 641025. = 0,(641025)
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.
Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.
пятьдесят четыре сотых в периоде.
9200/3 = 3066,666. = 3066,(6)
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.
Перевод периодической дроби в обыкновенную
Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.
Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.
Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:
Рассмотрим пример, в котором период дроби отличен от нуля.
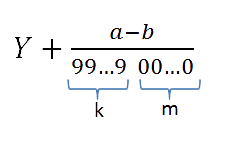
Как записать периодическую дробь 10,0219(37) в виде обыкновенной:
В нашем примере k = 2.
Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.
Теперь осталось подставить все найденные значения в формулу и получить ответ:
Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.
Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:
Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0
Перевод чистой периодической дроби в обыкновенную
Напомним: отличие чистой периодической десятичной дроби в том, что в ней сразу после запятой следует период.
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде. Вот так:
Перевод смешанной периодической дроби в обыкновенную
Отличие смешанной периодической десятичной дроби в том, что после запятой через одну или несколько цифр начинается период.
Чтобы записать смешанную периодическую дробь в виде обыкновенной, нужно из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числителе.
А в знаменатель нужно поставить число, которое содержит столько девяток, сколько цифр в периоде, нулей в конце и сколько цифр между запятой и периодом.
Например, запишем 2,34(2) в виде обыкновенной дроби: