Что нужно сделать чтобы сложить дроби с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями
Мы уже умеем сравнивать, складывать и вычитать дроби с одинаковыми знаменателями. Теперь рассмотрим сравнение, сложение и вычитание дробей с разными знаменателями.
Чтобы сравнить две дроби с разными знаменателями, надо:
1) привести данные дроби к общему знаменателю;
2) применить правило сравнения дробей с одинаковыми знаменателями.
Пример:
Сравним дроби 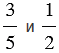
Приведем данные дроби к наименьшему общему знаменателю 10, получим:
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо:
1) привести данные дроби к общему знаменателю;
2) применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Примеры:
1) Найдем сумму 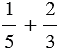
Наименьший общий знаменатель дробей 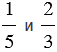
2) Найдем разность 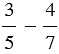
Наименьший общий знаменатель дробей 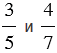
Для дробей, как и для натуральных чисел, выполняются свойства сложения:
1) Переместительное свойство:
2) Сочетательное свойство:
Сложение и вычитание смешанных чисел
Чтобы выполнить сложение смешанных чисел, нужно:
1) привести дробные части этих чисел к наименьшему общему знаменателю;
2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
Пример:
Чтобы выполнить вычитание смешанных чисел, нужно:
1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть;
2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Пример:
Обычно, примеры такого вида, как пример 2, записывают коротко:
Обратите внимание: если в результате сложения или вычитания дробей получается сократимая дробь, то нужно выполнить сокращение.
Поделись с друзьями в социальных сетях:
Сложение дробей.
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac<1><5>\) от всего пути. Во второй день они прошли от точки B до D или \(\frac<2><5>\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac<1> <5>+ \frac<2><5>\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
Ответ: туристы прошли \(\frac<3><5>\) всего пути.
Сложение дробей с разными знаменателями.
Нужно сложить две дроби \(\frac<3><4>\) и \(\frac<2><7>\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти общий знаменатель, а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac<3><4>\) нужно умножить на 7. Вторую дробь \(\frac<2><7>\) нужно умножить на 4.
В буквенном виде получаем такую формулу:
Сложение смешанных чисел или смешанных дробей.
Сложение смешанных дробей происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac<6><11>\) и \(1\frac<3><11>\).
Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac<1><8>\) и \(2\frac<1><6>\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac<1><8>\) на дополнительный множитель 3, а вторую дробь \(2\frac<1><6>\) на 4.
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух правильных дробей в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
Дробь \(\frac<5><7>\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac<2><7>\) и \(\frac<3><7>\).
Дробь \(\frac<58><45>\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac<2><5>\) и \(\frac<8><9>\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac<3> <11>+ \frac<5><11>\) б) \(\frac<1> <3>+ \frac<2><9>\).
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac<9><47>\) б) \(5\frac<1><3>\)
Пример №4:
Вычислите сумму: а) \(8\frac<5> <7>+ 2\frac<1><7>\) б) \(2\frac<9> <13>+ \frac<2><13>\) в) \(7\frac<2> <5>+ 3\frac<4><15>\)
а) \(8\frac<5> <7>+ 2\frac<1> <7>= (8 + 2) + (\frac<5> <7>+ \frac<1><7>) = 10 + \frac<6> <7>= 10\frac<6><7>\)
Задача №1:
За обедам съели \(\frac<8><11>\) от торта, а вечером за ужином съели \(\frac<3><11>\). Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
Дроби. Сложение дробей.
Сложение дробей с одинаковыми знаменателями.
Общая формула для сложения обыкновенных дробей и вычитания дробей с одинаковыми знаменателями:
Обратите внимание! Проверьте нельзя ли сократить дробь, которую вы получили, записывая ответ.
Сложение дробей с разными знаменателями.
Правила сложения дробей с разными знаменателями:
Примеры сложения дробей с разными знаменателями:
Сложение смешанных чисел (смешанных дробей).
Правила сложения смешанных дробей:
Пример сложения смешанной дроби :
Сложение десятичных дробей.
При сложении десятичных дробей процесс записывают «столбиком» (как обычное умножение столбиком), так чтобы одноимённые разряды находились друг под другом без смещения. Запятые обязательно выравниваем чётко друг под другом.
Правила сложения десятичных дробей:
1. Если нужно, уравниваем количество знаков после запятой. Для этого добавляем нули к необходимой дроби.
2. Записываем дроби так, чтобы запятые находились друг под другом.
3. Складываем дроби, не обращая внимания на запятую.
4. Ставим запятую в сумме под запятыми, дробей, которые складываем.
Обратите внимание! Когда у заданных десятичных дробей разное количество знаков (цифр) после запятой, то к дроби, у которой меньше десятичных знаков приписываем нужное количество нулей, для уравнения в дробях число знаков после запятой.
Разберёмся на примере. Найти сумму десятичных дробей:
Если сложение десятичных дробей вы освоили достаточно хорошо, то недостающие нули можно дописывать в уме.
Сложение и вычитание обыкновенных дробей
Давайте разберемся, как складывать и вычитать обыкновенные дроби. Данный навык необходим для решения множества задач как и в школьном курсе, так и при сдаче ОГЭ или ЕГЭ по математике. Итак, перейдем к рассмотрению различных примеров.
Сложение и вычитание дробей с одинаковыми знаменателями
Начнем с рассмотрения самого простого примера — сложения и вычитания дробей с одинаковыми знаменателями. В данном случае необходимо просто произвести действия с числителями — сложить их или вычесть.
При сложении и вычитании дробей с одинаковыми знаменателями знаменатель не изменяется!
Главное не производить никакие операции сложения и вычитания в знаменателе, но некоторые школьники забывают об этом. Чтобы лучше понять это правило, прибегнем к принципу визуализации, или говоря простыми словами, рассмотрим жизненный пример:
У Вас есть половина яблока — это ½ от всего яблока. Вам дают еще одну половину, то есть еще ½. Очевидно, что теперь у Вас целое яблоко (не считая, что оно разрезано 🙂 ). Поэтому ½ + ½ = 1, а не что-то другое, как, например, 2/4. Или же у Вас забирают эту половину: ½ — ½ = 0. В случае вычитания с одинаковыми знаменателями получается вообще особый случай — при вычитании одинаковых знаменателей, мы получим 0, а на 0 делить нельзя, и данная дробь не будет иметь смысла.
Приведем напоследок пример:
Сложение и вычитание дробей с разными знаменателями
Что же делать, если знаменатели разные? Для этого нам необходимо вначале привести дроби к одному знаменателю, а затем действовать как я указал выше.
Приводить дробь к общему знаменателю можно двумя способами. Во всех способах используется одно правило — при умножении числителя и знаменателя на одно и то же число дробь не изменяется.
Существует два способа. Первый — самый простой — так называемый «крест-накрест». Он заключается в том, что первую дробь мы умножаем на знаменатель второй дроби (и числитель и знаменатель), а вторую дробь умножаем на знаменатель первой (аналогично и числитель и знаменатель). После этого действуем как в случае с одинаковыми знаменателями — теперь они действительно одинаковые!
Предыдущий способ универсален, однако в большинстве случаев у дробей знаменателей можно найти наименьшее общее кратное — число, на которое делится и первый знаменатель и второй, причем самое маленькое. В данном методе нужно уметь видеть такие НОКи, потому что специальный поиск их достаточно ёмкий и уступает по скорости методу «крест-накрест». Но в большинстве случаев НОКи довольно хороши видны, если набить глаз и достаточно тренироваться.
Надеюсь, что теперь Вы в совершенстве владеете методами сложения и вычитания дробей!
Презентация к уроку
Цели:
Тип урока: урок-игра.
Оборудование: мультимедиа проектор, презентация «Сложение дробей с разными знаменателями», тест на компьютере (Приложение 1).
1. Организационный момент. Постановка целей урока
Учитель: Ребята! Сегодня мы с вами будем учиться складывать и вычитать дроби с разными знаменателями.
2. Повторение (разминка)
Учитель: Давайте сначала повторим, как сложить дроби с одинаковыми знаменателями и как сократить их. И заодно узнаем, что нам поможет понять эту тему.
Сказка ложь,
Но в ней намёк,
Добрым молодцам
И красным девицам урок.
3. Объяснение нового материала
В 3/9 царстве, в 3/9 государстве жили – были обыкновенные дроби. Были они разные.
– полтина,
– четь,
– полчеть,
– треть,
– полтреть,
полполтреть.
Действия с дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Поставил царь перед своими подданными проблему: найти интересные способы сложения дробей. И дал на раздумье одну ночь.
Первым вышел простак и предложил складывать дроби так:
Загудели дроби. Как же так?
Вторым вышел Тугодум. Он изобрел оригинальный способ:
Сократим 
Учитель: Научить складывать дроби этим способом можно любого: просто меняй знаменатели и подписывай их как дополнительные множители.
Учитель: А теперь попробуем сами выполнить сложение дробей этим способом. Какой способ сложения и вычитания дробей предложил Тугодум?
Чем хорош способ? Просто меняем знаменатели – легкий!
Чем плох? Сокращать ответ приходится.
А Зануда прочитал в умной книге, что сначала нужно найти НОК знаменателей.
24 : 3
24 : 6 = 4
Не по душе пришелся подданным этот способ.
Учитель: Потренируемся
4. Физкультминутка
Раз – подняться, потянуться
Раз – подняться, потянуться,
Два – нагнуть, разогнуться,
Три – в ладоши, три хлопка,
Головою три кивка.
На четыре – руки шире,
Пять – руками помахать,
Шесть – на место тихо сесть. (Можно повторить)
5. Объяснение нового материала (продолжение)
Тогда Умник говорит: 8 и 6 делятся на 2.
Вот увидите: этот способ в XXI веке будет самым удобным у шестиклассников!
Учитель: Действительно, это самый удобный способ нахождения дополнительных множителей: находим общий делитель знаменателей, делим на него знаменатели и подписываем результаты дополнительными множителями, меняя местами.
Учитель: Ребята! А вам понятен способ Умника? Давайте разберёмся, как находит дополнительные множители Умник. Потренируемся:
= (знаменатели делятся на 2)
= (знаменатели делятся на 4)
А царь спросил у Умника: «Как сложить три дроби?».
Учитель: А как вы предлагаете сложить эти дроби?
Но тут вышли три мудреца и предложили свой способ:
Делим больший знаменатель на два других:
Тогда 12 + 12 = 24 и проверяем снова.
24 : 6 = 4 24 : 8 = 3 24 : 12 = 2
Учитель: А сейчас потренируемся
6. Закрепление
Затем ученики выполняют тест (Приложение 1). Если тест по техническим причинам не работает (это может случиться в Office – 2003), то можно выполнить следующие действия:
1) Правой кнопкой мыши кликнуть на тест
2) Появится меню
3) Выбрать: свойства – безопасность – изменить – полный доступ – пользователь – полный доступ.
Если тест не работает, то учащимся предлагается выполнить самостоятельную работу.
Самостоятельная работа
Ответы:
Получится слово «УМНИКИ»
7. Итог урока
Если ты ленишься думать – пользуйся способом Тугодума (просто меняй знаменатели).
Если ты посообразительней – твой способ Умника.
Если ты – творец, то НОК дробей возникает у тебя в голове сразу.
Вот и сказочке конец, а кто слушал и понял – молодец!
8. Рефлексия
Учитель: А сейчас, отметьте пожалуйста, насколько был Вам полезен и интересен наш урок. Выберите нужный смайлик (предлагаются разные смайлики) и закрепите на доске.
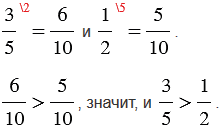
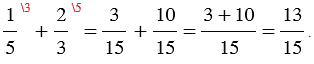
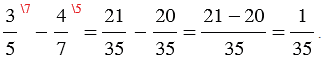
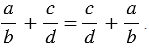
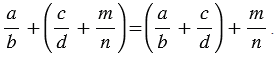
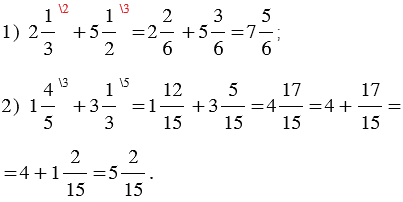
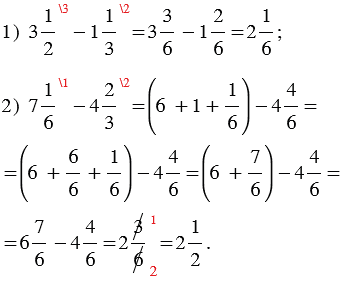
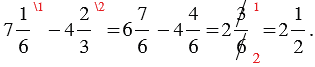






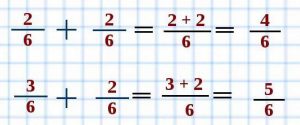
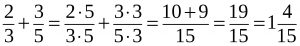
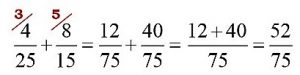

 – полтина,
– полтина,  – четь,
– четь,  – полчеть,
– полчеть,  – треть,
– треть,  – полтреть,
– полтреть,  полполтреть.
полполтреть.





 = (знаменатели делятся на 2)
= (знаменатели делятся на 2)  = (знаменатели делятся на 4)
= (знаменатели делятся на 4)



