Что нужно сделать чтобы узнать делимое
Как найти делимое
Как найти неизвестное делимое? Поможет правило:
А что делать, если правило вдруг забылось?
В этом случае нужно придумать несложный пример на деление, с его помощью понять, что делать для нахождения делимого, и применить этот вывод, чтобы найти неизвестное делимое в своем уравнении.
Например: 10:5=2. Здесь делимое — 10. Чтобы найти 10, надо 2 умножить на 5. Точно так же поступаем при решении своего примера.
Теперь посмотрим, как найти делимое, на конкретных примерах.
| x | : | 12 | = | 60 |
| дл | дт | ч |
Чтобы найти неизвестное делимое, нужно частное умножить на делитель:
| k | : | 7 | = | 11 |
| дл | дт | ч |
Для нахождения делимого частное умножаем на делитель:
Более сложные примеры, где помимо деления есть и другие действия, мы рассмотрим позже.
Нахождение неизвестных множителя, делимого или делителя
Урок 23. Математика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Нахождение неизвестных множителя, делимого или делителя»
Множитель, множитель, произведение. Делимое, делитель, частное.
Сегодня у нас непростой урок, ведь нам предстоит разобраться, как находить неизвестные: множитель, делимое или делитель. А для чего это надо уметь? Догадались? Ну конечно для того, чтобы уверенно решать уравнения! И мы, конечно же, решим несколько уравнений. Но прежде надо кое-что вспомнить.
Я предлагаю вам посмотреть на буквенную запись действия умножения.
А и Б в этой записи являются множителями, Ц – произведением. Понятно, что произведение мы получаем действием умножения. Это – целое, то есть наибольшее число. А вот множители являются частями. Значит, их мы находим обратным действием, делением.
То есть, если нужно найти неизвестный множитель, мы произведение делим на известный множитель.
А теперь посмотрим на буквенную запись деления:
Обычно, целое можно разделить на части. Поэтому К, делимое, является целым, а М и Н – это части. И, естественно, что целое мы находим умножением. Поэтому, если надо найти неизвестное делимое, мы перемножаем делитель с частным.
А вот делитель является частью. И, если надо найти неизвестный делитель, то его мы найдём, разделив делимое на частное.
Ну а теперь пришло время решать уравнения. Давайте разберём вот это уравнение:
Посмотрите, это у нас осложнённое уравнение. Поэтому, прежде всего, надо его упростить, то есть, выполнить действие в правой части уравнения. Сто двадцать шесть разделить на два равно шестьдесят три. Переписываем уравнение, заменив действие деления на его результат. Здесь надо найти неизвестный множитель. Чтобы найти неизвестный множитель, мы произведение делим на известный множитель.
Шестьдесят три делим на девять, получается семь.
Не забываем выполнить проверку уравнения. Сначала переписываем его, заменив икс на его значение, которое мы получили – семь. Семью девять – шестьдесят три. Сто двадцать шесть разделить на два – шестьдесят три. Левая и правая части уравнения равны, значит, уравнение решено верно. Решаем следующее уравнение:
Неизвестное делимое находим умножением.
Ну, а следующее уравнение я предлагаю вам решить самостоятельно.
Какой компонент здесь надо найти? Неизвестный делитель. А его мы находим
Проверьте, ребята, так ли решено у вас уравнение?
Видите, как помогает при решении уравнений знание правил.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Выучите их, ребята, и не забывайте пользоваться при решении уравнений. Пока! До новых встреч!
Деление чисел
Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.
Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:
Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:
Для записи деления используется знак : (двоеточие), который ставится между числами. Например:
Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (равно), после которого записывается полученный результат:
Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?
Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.
Решение можно записать так:
Пример. Решить примеры на деление с помощью схем.
2) 12 : 4 = 3, 12: 3 = 4.
Делимое, делитель и частное
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:
12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.
Частное — это число, которое получается в результате деления. Например, в записи:
4 — это частное. При этом сама запись 12 : 3 тоже называется частным.
Проверка деления
где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:
или умножить делитель на частное:
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, дорогие ребята. У нас в гостях крохотные человечки. Герои мультипликационного фильма Фиксики обитают внутри разнообразных технических устройств, приводят их в порядок в случае поломки. Мастера в любом деле добиваются успеха. Сегодня на уроке они расскажут много интересного.
Привет, друзья, сейчас мы отправимся в страну точных наук.
Встало солнышко давно,
Заглянуло к вам в окно,
На урок торопит вас –
Математика сейчас.
Меня зовут Симка. Мне девять лет. Я лучшая ученица в классе, самая смышленая и активная, прихожу на выручку друзьям. Ребята приготовьтесь решать примеры и задачи, учить и узнавать секреты математики.
С какой целью на уроке математики мы решаем примеры и задачи?
Правильно. Задачи нам необходимы для развития логики и мышления, а примеры – для того, чтобы быть математически грамотными людьми. Все это можно делать очень увлекательно.
Давайте начнем наше путешествие с рисунков. Возьмите тетрадь в клеточку, линейку и карандаш.
Таблица умножения с числами 6, 7, 8, 9
Чтобы таблицу умножения и деления запомнить быстро, надо ее представить, например, нарисовать.
Таблица умножения на 6
Представьте, что такое 3 умножить на 6. Это взять три клеточки шесть раз. Нарисуйте прямоугольник шириной три клеточки, длиной— 6. Нужно узнать, сколько всего клеточек получится. Здесь все сразу визуально видно: вот шесть столбиков по три клетки. А дальше, чтобы посчитать количество всех клеточек, надо сложить шесть троек.
Изобразите 6×3. Для этого нам нужно три раза взять по шесть клеточек. Обратите внимание, что фигура получается такая же, а разница только в том, как она разделена на клетки. Количество клеток не меняется, мы просто считаем по-разному. Именно поэтому от перестановки мест множителей произведение не меняется.
А теперь нарисуйте таблицу умножения на 6.
Запишите примеры столбиками:
Таблица умножения на 7
Один из самых простых способов ‒ это посчитать на пальцах.
Например, надо 8 x 7. Для этого:
1. На одной руке распрямите столько пальцев, насколько первый множитель больше 5, остальные пальцы подогните: 8 – 5 = 3.
Три пальца распрямите, два согните.
2. На второй руке также выполнить для второго множителя: 7 – 5 = 2.
Два пальца распрямить, а три согнуть.
3. Для результата взять столько десятков, сколько прямых пальцев на обеих руках вместе:
4. Количество единиц равно произведению согнутых пальцев:
Способ можно применять для умножения 6, 7, 8, 9.
Сколько будет 7 умножить на 8 или 8 умножить на 7, легко представить, если большой прямоугольник разбить пополам.
Запишите примеры в столбики:
Таблица умножения на 8
Запишите в столбик примеры.
Таблица умножения на 9
Вы уже догадались, что таблица умножения 9 и умножения на 9 похожи результатами, только множители меняются местами.
А теперь открою вам первый секрет — значения произведений на 9 зеркальны:
Второй секрет:
После знака равно первые цифры от 0 до 9 расставлены по порядку сверху вниз, а вторые цифры от 0 до 9 ‒ снизу наверх.
Третий секрет.
Если сложить количество десятков и единиц в каждом произведении, то получится 9.
Четвертый секрет.
Правило для табличных случаев умножения только на 9. Положите две ладошки перед собой. Отсчитайте слева направо палец, порядковый номер которого равен второму множителю, и согните его. Чтобы умножить, например, семь на девять, согните седьмой палец на руках, как на рисунке. Число десятков находится слева от согнутого пальца, а единиц — справа.
А какой палец загнёте при умножении 8 на 9? Правильно — восьмой. Проверьте себя: 8 x 9 = 7
Рассмотрите плакат. На нем показаны все случаи умножения на девять.
Пятый секрет.
Чтобы легче умножить любое число на девять, округлите 9 до 10. Выполните действие умножения, из полученного результата отнимите первый множитель.
Например, чтобы 8 x 9, сначала умножим 8 на 10, получим 80, а затем отнимем 8 и получим 72.
Делимое, делитель
Я — Папус, мастер на все руки. Мой талант проявляется в трудных ситуациях. Всегда готов к подвигу. Усердие, память помогают справляться с заданиями.
Запомните простые правила, которые расскажу.
Компоненты при делении называются так: делимое, делитель, частное.
Число, которое делят, — делимое,
насколько делят — делителем,
то, что получается в результате — частное.
Посмотрите на карточку:
У натуральных чисел может быть два или больше делителей.
Делители числа 42 – натуральные делители 1,2,3,6,7,14,21,42. Самый маленький делитель — 1, наибольший делитель — 42.
Вычислим делимое по делителю и частному
Задание 1. По этому правилу определите делимое в уравнении
Проверка:
Ответ: в = 72. Делимое равно 72
Задание 2. Делитель 7. Частное 8. Запишите, чему равно делимое.
Проверьте себя: 8 x 7=56
Как узнать, чему равен делитель?
Задание 3. Запишите и решите уравнение. Делимое 6. Частное 3.
Проверка:
Ответ: к = 2
Заполните таблицу. Связь между компонентами деления
Молодцы, вы хорошо потрудились. Пойдем дальше – будем догонять друзей и по пути немного отдохнем.
Физкультминутка
Чтобы отдохнуть, встанем на зарядку.
Начинаем выполнять все по порядку:
Руки в стороны, нагнулись,
До носочков дотянулись.
Разогнулись, приседаем и встаем,
Прыгаем на левой ножке,
Скачем-скачем по дорожке.
Умножение и деление с числами 1,0. Деление нуля на число
Сядьте ровно, потрите свои ушки, чтобы кровь активнее поступала в мозг. Я уверен, что вы справитесь отлично.
Умножение 0, умножение числа на 0
От 0 можно ожидать разные фокусы. Посмотрите, какой нуль коварный: когда его прибавляют, он не изменяет другое слагаемое, а когда умножают, превращает множитель в 0.
Для умножения числа на 0 применяют переместительный закон умножения:
Интересно, что получится, если 0 делить?
Деление нуля на число
0 конфет разделим между нами двоими, ничего не получим или 0. Можно ничего раздавать и на десять, и на сто друзей, все равно будет нуль.
Деление числа на 0
Разделите девять на нуль. Сколько получится?
Делимое девять должно получиться, если делитель 0 и частное перемножить. Но при умножении на нуль получим не девять, а нуль.
Пример не имеет решения.
Умножение и деление на 1
Решите данное уравнение X ∙ 1 = 48.
Какой множитель надо взять один раз, чтобы получилось 48?
48 умножить на 1, результат будет равен 48.
Значит, умножая на единицу, берешь множитель один раз и в результате выходить столько же.
Чтобы поделить на 1, надо все отдать одному. Например, 48 солдатиков подарить лучшему другу.
Получаем, что при делении на 1 делимое остается прежним.
Запомните простое правило, что при умножении и делении на один, число не меняется.
Ученик на контрольной работе решал примеры. Сыграйте роль учителя, проверьте задание.
Ученик допустил четыре ошибки. Он забыл правило умножения на 0 и 0. Таблицу умножения на 1 учить не надо. Число, которое умножают или делят на один, не меняется.
Ребята, вы хорошо потрудились. Раскрываю небольшой секрет, который должен знать каждый.
При умножении на числа, оканчивающиеся 0, дописывайте нулики к значению произведения. Если множитель 10, то в результате допишите один 0, а если умножаете на сто, то два.
А сейчас встречайте Масю, маму Нолика и Симки.
Дорогие друзья, рада всех видеть. Как все мамы, я занимаюсь заготовкой урожая, поэтому знаю много об овощах, фруктах и ягодах. Мой жизнерадостный уравновешенный характер помогает соблюдать чистоту и порядок, а высокая квалификация позволяет решать задачи.
Решение задач с понятиями «масса» и «количество»
Мои ребята любят печеную картошку. А знаете ли вы, что в Россию картофель завез Петр Первый ещё в 17 веке.
В картофеле много витамина В6, витамина С, калия, фосфора и других полезных микроэлементов. Он богат клетчаткой и полезен для пищеварения и сосудов. Но жаренная на масле картошка вредит сосудам и сердцу. Лучше употреблять ее вареной или печеной без жира.
На рынке купили картофель в сетках. Давайте опишем покупку с помощью математики.
Нам понадобится величина. Это такое свойство предметов, которое можно измерить и результат записать с помощью числа. Величина, характеризующая вес тела, называется масса.
В качестве единицы массы часто используют килограмм. В 1799 году ученые придумали такую мерку для измерения веса.
Чему равна масса одной сетки?
Назовите количество сеток.
Задача 1. Определите массу всей покупки.
Как узнать, сколько всего килограммов картофеля купили? 10 ∙ 3 = 30 кг
Задача 2. Для консервирования купили шесть коробок помидоров весом 54 килограмма. Определите массу одной коробки.
Рассуждаем так: 54 кг – это масса всех коробок, таких коробок – 6.
Массу одной коробки узнаем действием деления.
Ответ: 9 кг весит одна коробка.
Задача 3.
В одну банку входит 8 кг варенья. Сколько нужно банок, чтобы разлить в них поровну 56 кг варенья?
Рассуждаем так: разливаем всю массу варенья по 8кг на банку действием деления.
Решение.
Ответ: нужно 7 банок.
Запомните правила, как решаются задачи на массу и количество.
Задача 4.
В подвал на хранение разложили 36 кг слив в 4 ящика. Сколько яблок в 6, а груш в 7 таких ящиках, если масса каждого ящика с фруктами одинаковая?
Что нужно сделать?
Как представить краткую запись?
Начертите столбцы, занесите условие и вопрос задачи построчно.
Что надо знать, чтобы найти массу 6 ящиков? 7 ящиков?
Массу одного ящика
Каким действием узнаете массу 6 ящиков? 7 ящиков?
Решите задачу, какая масса ящиков с яблоками и грушами выражением.
Ответ: в 6 ящиках 54 кг яблок, в 7 ящиках 63 кг груш.
Это интересно: Зимой малиновое варенье становится не только лакомством, но ещё и крайне эффективным лекарством. Оно содержит витамин С, понижает температуру и укрепляет иммунитет.
Повторим, как решать задачи с величинами цена, количество, стоимость
Задача 5.
Мама купила 7 кг варенья и 8 кг свежих ягод по одинаковой цене. За варенье она заплатила 700 рублей. Сколько стоили ягоды?
Что поможет ответить на вопрос задачи?
Решение:
700 : 7 = 100 (руб.) – цена 1 кг варения
100 ∙ 8 = 800 (руб.) – стоимость ягод.
Ответ: 800 рублей.
Вы, ребята, молодцы. Есть у нас условный знак – нужно пальцы сделать так.
Урок наш подходит к концу и нам нужно подвести его итог:
сегодня я научился
Все хорошо потрудились. Спасибо.
В материалах урока использованы кадры из м/с «Фиксики», 2010
Деление натуральных чисел
Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.
Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?
Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.
Деление – это арифметическое действие, которое состоит в нахождении одного из сомножителей при помощи данного произведения и второго сомножителя.
Делимое – это число, которое мы делим на другое. Это то самое произведение, которое нам дано.
Делитель – это число, на которое мы делим делимое. Это данный нам один из множителей.
Частное – это результат действия деление, то есть, искомый нами второй сомножитель.
На записи действие деление обозначается: двоеточием ( \(\textcolor
Так, решение нашей задачи можно записать следующими способами:
При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.
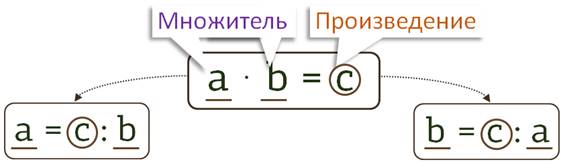
Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: \(\textcolor
Компоненты действия деление:
Деление с остатком и неполное частное
К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( \(\textcolor
Итак, деление с остатком – это нахождение такого наибольшего целого числа, умножив которое на делитель, мы получим число, максимально близкое к делимому, но не превосходящее его. Это искомое число называется неполное частное. Разница между делимым и неполным частным называется остаток.
Остаток всегда меньше делителя!
Связь деления с умножением, сложением и вычитанием
Когда мы выполняем находим произведение двух чисел, эти числа нам известны, а от нас требуется найти результат действия умножение. При делении (без остатка) нам известно произведение двух чисел, а найти нужно такое число, которое при умножении на известное данное число дает это самое произведение.
Следовательно, действие деление является обратным действию умножения.
Справедливо также и обратное, что действие умножение обратно действию деления. Таким образом:
Умножение и деление – это взаимно обратные действия.
Связь деления с умножением, а также со сложением и вычитанием прекрасно видна, если рассмотреть, как с помощью этих действий можно выполнить действие деление.
Деление двух чисел при помощи сложения
Деление двух чисел при помощи вычитания
То есть, 69 от 345 можно отнять 5 раз, поэтому \(\textcolor
Деление двух чисел при помощи умножения
При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345 :
Но эти три способа очень громоздки, особенно если частное представляет собой очень большое число. Их нужно знать только для того, чтобы понимать суть действия деления, суть тех задач, которые решаются посредством него.
Общий принцип деления в столбик
Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.
Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.
Далее записываем известные компоненты деления следующим образом:
и начинаем вычисление:
1. Берем первое неполное делимое и пытаемся его разделить на делитель.
Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.
Записываем в частное первую найденную цифру разряда тысяч, а под неполным делимым пишем результат произведения неполного частного и делителя. И сразу же находим остаток от этого действия, т.е. вычитаем из неполного частного результат этого произведения.
В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor
В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.
2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.
3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.
4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.
Рассмотрим еще один пример. \(\textcolor
1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.
Итак, запомните, что каждое неполное делимое образует в частном одну цифру соответствующего разряда и что даже если неполное делимое меньше делителя, то в частном все равно нужно записать нулевой результат этого действия.
Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.
Деление на числа, заканчивающиеся нулями
Как и в случае с умножением, деление чисел облегчается, если делитель заканчивается одним или несколькими нулями. Рассмотрим два возможных случая:
Рассмотрим первый случай.
Деление на единицу с любым количеством нулей
Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.
Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.
Деление на число, оканчивающееся нулями
Рассмотрим на примере \(\textcolor
Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.
Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.
Проверка деления
Так как делимое – это делитель, умноженный на частное и плюс остаток, что следует из определения деления, то результат выполнения деления можно проверить умножением.
Если в результате действия деления не получилось остатка, то деление можно проверить и делением. Действительно, если делимое – это произведение делителя и частного, то разделив делимое на частное (один из сомножителей), мы должны получить второй сомножитель, то есть, делитель.
Свойства деления
Свойства деления я представлю двумя группами:
Давайте рассмотрим каждую группу подробнее.
Действия деления с единицей и нулем
При делении числа на единицу получается то же самое число.
Действительно, разделить число на единицу означает узнать, сколько единиц содержится в данном числе. А количество единиц в числе – это не что иное, как само это число.
И ли вот, например, если 10 яблок нужно раздать одному человеку ( 10 поделить на 1 ), то ему все эти 10 яблок и достанутся, правда?
При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).
В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.
Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.
При делении нуля на любое число, отличное от нуля, в результате будет нуль.
Разделить нуль на число означает найти такое число, умножив которое на данный делитель, мы получим в результате нуль. А такое число только одно – это нуль.
На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.
При делении каких угодно чисел делителем может быть любое число, кроме нуля.
Рассмотрим два случая: когда нулём является только делитель, и когда делимое и делитель оба нули.
Распределительные свойства деления
Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
\(\textcolor
При этом подразумевается, что все действия деления получаются без остатка.
Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
\(\textcolor
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.
Например: \[\textcolor
Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
\(\textcolor
Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
\(\textcolor
При этом предполагается, что при всех этих делениях не получается остатков.
На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.
Изменение частного при изменении делимого и делителя
При рассмотрении изменений частного в результате изменений делимого и делителя предполагается, что действие деление происходит без остатка. В противном случае изменения могут быть не такими, о которых идет речь ниже.
При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.
Если мы в примере \(\textcolor
Если мы в этом же примере \(\textcolor
При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.
Действительно, изменение делителя означает, что делимое необходимо разделить на большее или меньшее количество равных частей. Соответственно, если нужно разделить на большее число частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее число частей, то каждая часть будет крупнее.
В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.
При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.
Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось это, или нет.