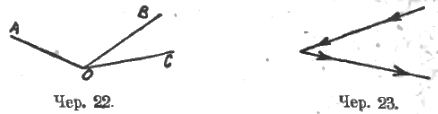Что нужно сделать с лучом чтобы получился отрезок ответ

Что такое луч в математике

Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.

Луч — геометрическое понятие

Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.

На картинке вы можете посмотреть, что такое луч и как он выглядит:

Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.

Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.

Отличия луча от прямой и от отрезка

В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.

В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.

В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.

Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:

Взаимное расположение лучей

Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.

На рисунке начало для лучей — общая точка A.

По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.

Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.

Дополнительные лучи — это фигуры, которые обладают такими признаками, как:

Можно ли сравнить два луча?

Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.

Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.

Луч — альтернативные значения слова

Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.

Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.

Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:

В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.

Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.

Источник

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Обозначение прямой

Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Рис. 2 Обозначение прямой с несколькими точками

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

Рис. 5 Пересечение прямых

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

Луч имеет второе название – полупрямая.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 22

Источник

Математика

Ко всему этому изучению рассматриваемых комбинаций следует присоединить (в разные моменты) упражнения: 1) в построении прямой через 2 данные точки, 2) в построении сколько угодно лучей, исходящих из одной точки и 3) в построении отрезка без прямой. В последнем построении вводится некоторая условность: изображение ––––––––– принято считать изображением прямой линии – бесконечной, а изображение |––––––| принято считать изображением прямолинейного отрезка.

Также точно, начиная с палочек, нетрудно привести в ясность те операции, какие нужны для выполнения вычитания отрезков.

В соответствующие моменты на протяжении всех этих занятий учащиеся должны выполнить ряд упражнений. Вот наиболее существенные из них.

Все эти упражнения необходимы, так как должно стремиться к тому, чтобы в будущем, когда придется иметь дело с более сложными комбинациями, учащиеся легко могли бы смотреть на известный отрезок, как на сумму или разность других отрезков.

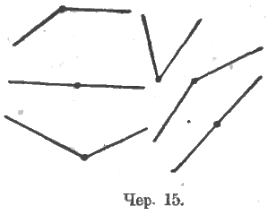
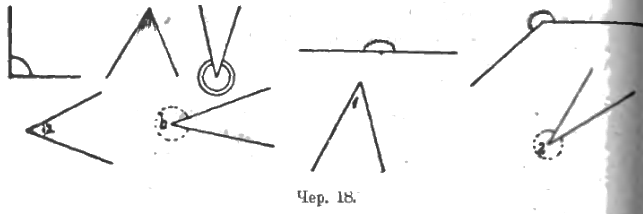
Переходим к углам. Строится несколько раз учащимися фигура, состоящая из точки и двух лучей, из этой точки выходящих (чер. 15). Каждой из этих фигур дается название «угол».

Учащиеся устанавливают, что они умеют строить угол: надо построить точку и из нее 2 луча. Вводятся названия: «вершина угла», «сторона угла»; последние показываются палочкою – ученики проводят ею от вершины по соответствующему лучу.

Выясняется, что стороны углов идут без конца, а поэтому угол остается тот же, если стороны «нарисованы» или немного длиннее или короче.

Среди углов, оказывается, имеется особый угол. Учащиеся могут установить его существование или из рассмотрения различных углов, построенных ими самими (на доске), – см. предыдущий чертеж – или при помощи опыта вращения палочки (чер. 16).

Держим палочки рукою в том месте, где они сходятся, и одну из них вращаем. Особенный угол получается тогда, когда стороны угла окажутся расположенными по прямой линии (эта особенность подмечается самими учениками и высказывается ими). Называем этот особенный угол именем «выпрямленный» или «развернутый»; показываем его вершину и стороны; строим простейшим способом выпрямленный угол (прямую линию и на ней точку). Учащиеся упражняются в обозначении углов при помощи трех букв.

Далее можно обратить внимание на тот факт (и желательно, чтобы учащиеся сами это увидали), что плоскость делится углом на 2 области (на 2 части) – см. чер. 17, где одна область затушевана. Про одну из этих областей мы говорим, что она лежит внутри угла (внутренняя область угла), а о другой, – что она лежит вне угла (внешняя область). Какую именно счесть за внутреннюю область, а какую за внешнюю – это безразлично. Если мы возьмем кусок бумаги, изображающий собою плоскость, если на нем построим угол и разрежем этот кусок по сторонам угла, то плоскость разделится на 2 части.

Чтобы рассматривать угол, приходится рассматривать одну из этих частей, а какую именно – безразлично: на каждой из них можно показать и вершину и стороны угла. Станем теперь рассматривать углы с присоединенными к ним внутренними областями (чер. 18). Чтобы на чертеже видеть, какую именно часть плоскости мы принимаем за внутреннюю область угла (и присоединяем ее к углу), условимся отмечать эту область каким-либо способом: или рисовать по этой области какую-нибудь кривую от одной стороны до другой или немного затушевывать эту область или, что в дальнейшем чаще всего будет встречаться, на этой области будем ставить ту малую букву или цифру, которыми будем иногда называть рассматриваемые углы.

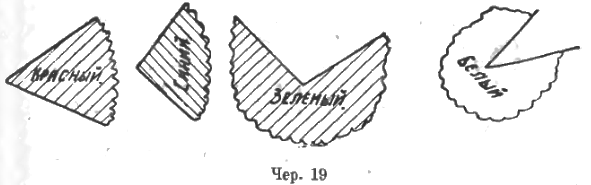
Приступаем к сравнению углов: если имеем два угла, то можно установить, что или эти углы равны или неравны и в последнем случае один угол больше другого. Следует привести в отчетливость тот процесс наложения одного угла на другой, при помощи которого это делается. Для этой цели удобно сначала иметь дело с моделями углов, вырезанных из цветной бумаги (каждая модель дает угол с его внутреннею областью) (чер. 19).

Во время упражнений с равными и неравными углами удобно установить, в каком смысле употребляется в геометрии термин « равные фигуры».

Здесь необходимы упражнения с вырезанными из бумаги моделями углов; оперируя с этими моделями, учащиеся учатся, 1) сравнивать два угла, 2) отличать сразу углы, большие выпрямленного, и углы, меньшие выпрямленного (полезно, хотя обычно это и не принято, сравнение углов не ограничивать только углами, меньшими выпрямленного). 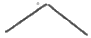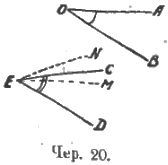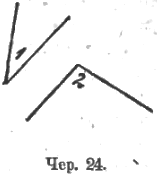Также точно желательны упражнения вроде следующего: построен угол (например, ), отметить его внутреннюю область так, чтобы получился: 1) угол, меньший выпрямленного, или чтобы получился 2) угол, больший выпрямленного.

Переходим далее к сложению и вычитанию углов. Здесь имеют место соображения, аналогичные данным при описании методики сложения и вычитания отрезков. Так же точно надо привести в отчетливость процессы сложения и вычитания углов (их описание пропускаем), выработать хотя бы некоторый навык видеть на чертеже сумму и разность углов. Так, при условии, что имеем дело лишь с углами, меньшими выпрямленного, мы на чер. 22 видим: 1) ∠ AOB + ∠ BOC = ∠ AOC (следует каждый слагаемый угол и угол сумму показывать; при этом это показывание полезно выполнять палочкою, проводя ее, как показывает стрелка (чер. 23), по сторонам угла); 2) ∠ AOC – ∠ AOB = ∠ BOC и 3) ∠ AOC – ∠ COB = ∠ BOA (также надо показывать уменьшаемый угол, вычитаемый и угол разность).

Как можно подметить, все вышеизложенное направляется идеею, что и отрезки и углы суть самостоятельные объекты, с которыми мы учимся выполнять известные операции, не стремясь сводить дело к арифметике, к числам.

Сложение и вычитание углов также должно начаться с выполнения соответствующих процессов над моделями углов, вырезанными из бумаги.
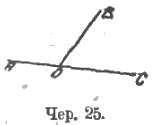
Упражнение: даны два угла, ∠1 и ∠2 (чер 24), найти их сумму (или разность), – может быть или выполняемо теперь при помощи изготовления бумажных моделей данных углов или может быть отнесено к более позднему моменту курса, к тому именно, когда будет введен в дело круг и установлена возможность строить при помощи кругов угол, равный данному.

Упражняясь над сложением углов, учащиеся могут прийти к установлению возможности случая, когда от сложения двух углов в сумме получатся выпрямленный угол. Установить такую возможность можно опять-таки при помощи операций над моделями углов, а затем построить соответствующий чертеж.

Здесь, как то уже было указано в п. 6, можно дать название «смежные» углы (чер. 25), описать их расположение (общая вершина, одна сторона общая, а две другие составляют прямую линию), но здесь нет места каким-либо доказательствам каких-либо теорем.

Далее ставится задача дополнить данный угол до выпрямленного. В п. 3 уже выяснено, что решение этой задачи приводит к установлению свойства вертикальных углов. Поэтому здесь на этом не останавливаемся.

Источник

Математика. 5 класс

Конспект урока

Прямая, луч, отрезок

Перечень рассматриваемых вопросов:

— понятия «прямая», «луч», «отрезок»;

— отличия прямой, луча, отрезка;

— прямая, луч, отрезок на чертежах, рисунках и моделях.

Отрезок – часть прямой, ограниченный двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.

Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).

Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.

Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.

Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.

Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.

Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.

Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.

Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.

Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя.

Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.

Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.

В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.

Заметим, что два отрезка называются равными, если они совмещаются при наложении.

Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.

Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: добавление подписей к изображениям.

Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.

№ 2. Тип задания: подстановка элементов в пропуски в тексте.

Вставьте в текст нужные слова.

Через__________ две____________ можно провести только одну _________.

Слова: любые; точки; прямую; ломаную.

Правильный ответ: через любые две точки можно провести только одну прямую.

Источник

Основы геометрии

Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.

Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.

Точка

Точка — это основная и самая простая геометрическая фигура.

В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.

В тексте точку обозначают следующим символом: « (·) A » — точка « А ».

Прямая

Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.

Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.

Способы обозначения прямых

Способы обозначения лучей

Отрезок

Основное свойство отрезка — это его длина.

Длина отрезка — это расстояние между его концами.

В математике отрезок обозначается заглавными латинскими буквами.

Ломаная

Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.

Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.

Звенья ломаной — это отрезки ломаной.

В математике ломаная обозначается заглавными латинскими буквами.

Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.

KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см

Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол.

Источник