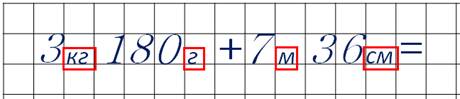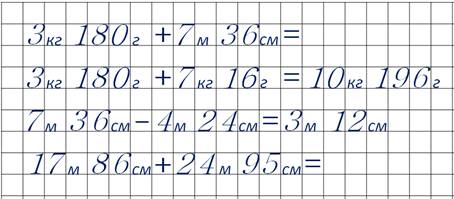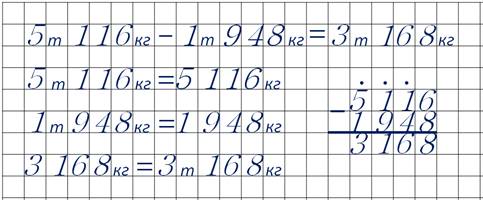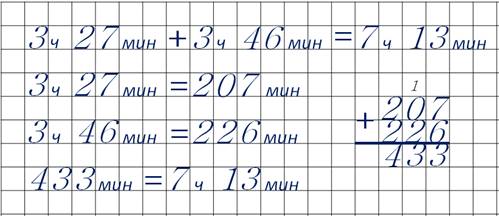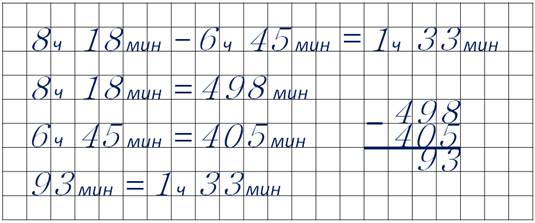Что нужно учитывать при сложении и вычитании физических величин

Что нужно учитывать при сложении и вычитании физических величин

Из курса математики нам известны действия, которые можно производить над числами. Складывать, вычитать и сравнивать в математике можно любые числа. Такие действия над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину. Например:

Во всех трех случаях мы производили действия над однородными физическими величинами. Складывали длину с длиной, вычитали из массы массу, сравнивали промежуток времени с промежутком времени. Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг!

А вот умножать и делить можно не только однородные, но и разные физические величины. Например:

1) 10 кг/2 кг = 5. Здесь делятся не только числовые значения (10 : 2 = 5), но и единицы физических величин (кг : кг= 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.

3) 10 м/2 с = 5м/с. В результате деления двух разных физических величин — длины l=10м на промежуток времени t=2 с, получилась новая физическая величина 5 м/с. Ее числовое значение равно 5, а единица новой физической величины м/с. Эта физическая величина с υ = 5 м/с — скорость.

4) 10 м/2 с = 20 м/4 с. Знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если 10 м 20 м о м сравнить 10 м/2 с и 20 м/4 мин. Здесь м/с≠м/мин.

Подумайте и ответьте

1. Что необходимо учитывать при сложении и вычитании физических величин? Каким будет результат их сложения и вычитания?

2. Какие физические величины можно сравнивать между собой? Приведите примеры.

3. Можно ли делить и умножать разные физические величины? Что получится в результате?

4. Определите, значение какой физической величины получится в результате:

Интересно знать!

Большие единицы времени — год и сутки — дала нам сама природа. Но час, минута и секунда появились благодаря человеку.

Принятое в настоящее время деление суток восходит к глубокой древности. В Вавилоне применялась не десятичная, а шестидесятерич-ная система счисления. Шестьдесят делится без остатка на 12, отсюда у вавилонян деление суток на 12 равных частей. В Древнем Египте было введено деление суток на 24 часа. Позже появились минуты и секунды. То, что в 1 часе 60 минут, а в 1 минуте 60 секунд, — также наследие шестидесятеричной системы Вавилона.

Определение единиц времени является очень важным. Основная единица времени — секунда — сначала была введена как 1/86400 доля суток, а затем из-за непостоянства суток — как определенная доля года. В настоящее время эталон секунды связан с частотой излучения атомов цезия.

Примеры решения задач

Решение. Однородными физическими величинами в данном случае являются массы тел: m₁ = 120 г и m₂ = 0,048 кг. Для выполнения операции сложения физические величины необходимо выразить в одних единицах. Одну из масс, например т2, выразим в единицах, в которых записана масса ть т. е. в граммах (г). Так как

1 кг = 1000 г, то m₂ = 0,048 кг = 0,048- 1000 г = 48 г.

Ответ: результатом сложения является масса m = 168 г.

2. Определите физические величины, получившиеся в результате следующих действий: 1) 0,6 г/см 3 • 5 см 3 ; 2) 40 см • 0,25 м.

Решение. 1) Найдем произведение двух физических величин, перемножив их числовые значения и единицы:

0,6 г/см 3 • 5 см 3 = (0,6 • 5) ( г/см 3 • см 3 ) =3 г.

Мы получили физическую величину — массу m = 3 г. 2) Чтобы выполнить умножение двух однородных физических величин, необходимо выразить их в одних единицах, например в сантиметрах (см):

Ответ: 1) в результате умножения двух физических величин разного рода (плотности и объема) получена третья физическая величина — масса m = 3 г;

Упражнение 2

1. Какие из приведенных значений величин можно складывать? Выполните сложение и запишите результат:

2. Какие из приведенных значений величин можно вычитать? Выполните вычитание и запишите результат:

3. Сравните длины отрезков: l₁=48 см, l₂ = 0,48 дм, l₃ = 48 мм. Какие отрезки имеют равную длину? Какой отрезок имеет наибольшую Длину? Изобразите отрезки в тетради.

4. Определите, какая физическая величина получается в результате следующих действий:

Источник

Сложение и вычитание величин

При сложении или вычитании однородных величин единицы измерения величин не меняются.

Чтобы найти сумму или разность однородных величин, надо произвести действия над их численными значениями и, к полученному результату, приписать единицу измерения величины.

Пример 1. Найти сумму 37 м + 12 м:

Если величины состоят из двух единиц измерения, то можно либо сразу произвести действия над их численными значениями, по необходимости переводя промежуточный результат из одной единицы измерения в другую. Либо сначала привести их к одной единице измерения, а потом произвести нужные вычисления.

Пример 1. Найти сумму величин:

12 кг 729 гр + 9 кг 435 гр.

Сложение будем производить столбиком. Напишем числа так, чтобы килограммы были записаны под килограммами, а граммы — под граммами.

Складываем единицы граммов: 9 + 5 = 14 (единиц граммов или 1 десяток граммов и 4 единицы). Пишем под единицами граммов цифру 4 и 1 десяток запоминаем.

Складываем десятки граммов: 2 + 3 = 5 (десятков граммов). К этим 5 десяткам надо прибавить ещё один, который мы получили при сложении единиц: 5 + 1 = 6 (десятков граммов). Пишем под десятками граммов цифру 6.

Складываем сотни граммов: 7 + 4 = 11 (сотен граммов или 1 тысяча граммов и 1 сотня). Пишем под сотнями граммов цифру 1 и 1 тысячу запоминаем.

Складываем единицы килограммов: 2 + 9 = 11 (единиц килограммов). К этим 11 единицам надо прибавить ещё 1, которую мы получили при сложении сотен граммов: 11 + 1 = 12 (единиц килограммов или 1 десяток и 2 единицы). Пишем цифру 2 и 1 десяток запоминаем.

Складываем десятки килограммов: 1 + 0 = 1 (десяток килограммов). К этому десятку надо прибавить ещё один, который мы получили при сложении единиц килограммов: 1 + 1 = 2 (десятка килограммов). Пишем под десятками килограммов цифру 2.

Всего получили 22 кг 164 гр.

Данное выражение можно вычислить по другому: сначала привести обе величины к одной единице измерения:

12 кг 729 гр = 12729 гр;

9 кг 435 гр = 9435 гр;

а затем численные значения величин можно сложить столбиком:

полученный результат, при необходимости, можно привести обратно к двум единицам измерения:

22164 гр = 22 кг 164 гр.

Пример 2. Найти разность величин:

Вычитание будем производить столбиком. Напишем числа так, чтобы километры были записаны под километрами, а метры — под метрами:

Всего получили 2 км 619 м.

Данное выражение можно вычислить по другому: сначала привести обе величины к одной единице измерения:

9 км 528 м = 9528 м;

6 км 909 м = 6909 м;

а затем выполнить вычитание столбиком:

полученный результат, при необходимости, можно привести обратно к двум единицам измерения:

Источник

Действия над физическими величинами

План-конспект урока по теме « Действия над физическими величинами. Решение задач »

Тема: « Действия над физическими величинами. Решение задач »

Образовательная : формирование практических умений по выполнению действий над физическими величинами;

Развивающая : совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;

Воспитательная : прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.

Тип урока: обобщение и систематизация знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика : учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2017;

Организационный момент(4 мин)

Актуализация опорных знаний(3 мин)

Изучение нового материала (13 мин)

Первичная проверка понимания (12 мин)

Закрепление полученных знаний (8 мин)

Организационный момент (проверка присутствующих в классе, озвучивание темы и основных целей урока )

Актуализация опорных знаний

В математике можно складывать, вычитать и сравнивать любые числа. А какие же действия можно производить над физическими величинами?

Изучение нового материала

Действия сложения, вычитания и сравнения над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.

Во всех трех случаях мы производили действия над однородными физическими величинами. Складывали длину с длиной, вычитали из массы массу, сравнивали промежуток времени с промежутком времени. Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг!

А вот умножать и делить можно не только однородные, но и разные физические величины. Например:

10 кг ÷2 кг = 5. Здесь делятся не только числовые значения (10 ÷ 2 = 5), но и единицы физических величин (кг ÷ кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.

10 м ÷ 2 с = 5 м/с. В результате деления двух разных физических величин — длины l = 10 м на промежуток времени t = 2 с, получилась новая физическая величина 5 м/c. Ее числовое значение равно 5, а единица новой физической величины — м/c. Эта физическая величина v = 5 м/c — скорость.

10 м ÷ 2 с = 20 м ÷ 4 с. Знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 10 м ÷ 2 с и 20 м ÷ 4 мин. Здесь м/с ≠ м/мин.

Первичная поверка понимания

Что необходимо учитывать при сложении и вычитании физических величин? Каким будет результат их сложения и вычитания?

Какие физические величины можно сравнивать между собой? Приведите примеры.

Можно ли делить и умножать разные физические величины? Что получится в результате?

Определите, значение какой физической величины получится в результате:

Далее рассматриваются примеры решения задач из учебника

Решение задач из упражнения 2

Итак, подведем итоги. Что нового вы сегодня узнали на уроке?

Какие сложности у вас возникли?

Организация домашнего задания

§6,ответить на контрольные вопросы; упр. 2(4 задание).

Сегодня на уроке я узнал…

Знания, которые я получил на уроке, пригодятся

Источник

Математика. 4 класс

Конспект урока

Математика, 4 класс

Урок №23. Сложение и вычитание значений величин

Перечень вопросов, рассматриваемых в теме:

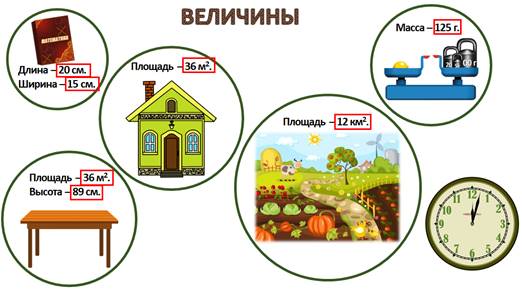
Величина – это то, что можно измерить (длина, ширина, объём и т.д.) и результат представить в виде числа.

Единица измерения – это величина, в которой выражаются другие, однородные с ней величины. Например: метр, литр и др.

Обязательная литературы и дополнительная литература:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика: 4 класс: учебник в 2 ч. Ч.1. – М.: Просвещение, 2015. – С.67-68

2. Ефимова А. В., Гринштейн М. Р. 214 задач и примеров по математике для 4 класса. – СПб: Издательский Дом «Литера», 2008. – С.7-10

3. Рудницкая В. Н. Математика: 4 класс. Контрольные и измерительные материалы.– М.: Издательство «Экзамен», 2014. С.19-23.

Теоретический материал для самостоятельного изучения

Рассмотрите выражения и найдите лишнее

524м 95см +29м 85см

— Почему? (Выражение не содержит величин.)

Какие действия с величинами мы уже умеем выполнять? (Сравниваем, преобразуем, вычитаем, складываем)

С первым выражением мы легко справляемся, а вот второе вызвало затруднение. Почему? Первое мы посчитали устно, а второе в уме выполнить трудно.

— Какова же цель нашего урока? (Научиться складывать и вычитать величины, выраженные разными единицами)

Попробуем выполнить сложение письменно. Что для этого нужно сделать? ( Привести к одинаковым единицам)

524 м 95 см = 52 495 см

29 м 85 см = 2 985 м, запишем выражение в столбик и выполним сложение

Получаем 55 480 см. Выразим результат в более крупных единицах 55480 см = 554 м 80 см, значит:

524 м 95 см +29 м 85 см = 554 м 80 см

25 т 204 кг – 9 т 975 кг

Переведём величины в одинаковые единицы

25 т 204 кг = 25 204 кг

9 т 975 кг = 9 975 кг

Запишем выражение столбиком

Получилось 15 229 кг. Переведём в более крупные единицы 15 229 кг = 15 т 229 кг, значит:

25 т 204 кг – 9 т 975 кг = 15 т 229 кг.

Составим алгоритм письменного сложения и вычитания величин:

Вывод 1: Величины с разными единицами складываются и вычитаются как обычные числа.

Попробуем решить ещё один пример:

5ч 23 мин + 12 кг 300 г

Этот пример не имеет решения, так как нужно сложить разные величины

Вывод 2: Выполнять действия можно только с однородными величинами.

Выполним несколько тренировочных заданий:

Решение: 368 км 576 м

368 км 576 м – 214 км 865 м = 368 576 – 214 865 = 153 711 (м)

Источник

Сложение и вычитание величин

Урок 18. Математика 4 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Сложение и вычитание величин»

Вы знаете, сегодня у меня возникло затруднение. Дело в том, что наш домовой Матюша отмечает день рождения. Он пригласил меня в гости, и я через восемь часов двадцать три минуты должна быть у него. Но мне ещё надо решить сто сорок семь задач и двести девяносто восемь примеров на сложение и вычитание величин. Решение задач займёт три часа двадцать семь минут, а решение примеров три часа сорок шесть минут. Вот я и подумала: не опоздаю ли я в гости к Матюше? Ведь опоздания в нашем наиточнейшем царстве Математики считаются тяжким преступлением.

Надо срочно всё рассчитать. И начну я, пожалуй, с примеров. Но сначала надо вспомнить, что такое «величины».

Многие объекты или явления можно измерить. Например, можно измерить длину и ширину книги, площадь стола, дома, огорода. Можно взвесить какие-то предметы и узнать их массу. Можно даже измерить какой-то промежуток времени.

Числа, которые при этом получаются, можно назвать величинами. Возле этих чисел всегда стоят буквенные обозначения, которые и подсказывают, в каких величинах измеряли объект или явление. Эти буквенные обозначения называют «наименования величин», а числа с такими наименованиями называют «величинами» или «именованными числами».

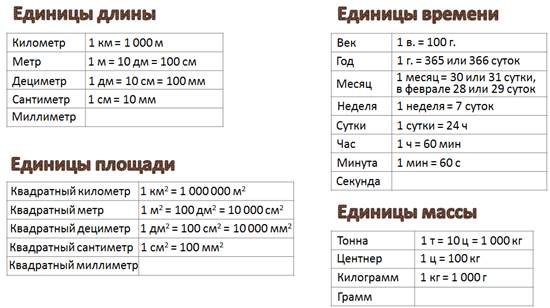
Давайте вспомним единицы измерения величин, с которыми вы уже знакомы, и соотношения между ними:

Единицы длины. Единицы площади. Единицы времени. Единицы массы.

Ну а теперь я начну решать примеры на сложение и вычитание величин.

Ой, что за странный пример! Наверное, царица Математика решила надо мною подшутить, а, заодно, проверить мою внимательность. Эти величины нельзя складывать друг с другом. Ведь сложение и вычитание величин возможно только в том случае, если эти величины однородные. Единицы массы можно складывать или вычитать только с единицами массы, единицы длины – только с единицами длины, единицы времени – с единицами времени.

А вот к единицам массы прибавить единицы длины совершенно невозможно.

Переходим к следующему примеру.

К трём килограммам ста восьмидесяти граммам прибавить семь килограммов шестнадцать граммов. Ну, этот пример легко решить. Килограммы складываем с килограммами. Их получается десять. Граммы складываем с граммами. Их сто девяносто шесть. Ответ: десять килограммов сто девяносто шесть граммов.

Следующий пример. Из семи метров тридцати шести сантиметров вычесть четыре метра двадцать четыре сантиметра. Это тоже легко! Из метров вычитаем метры., из сантиметров – сантиметры. Получается три метра двенадцать сантиметров.

Так-так следующий пример.

Складываем семнадцать метров восемьдесят шесть сантиметров и двадцать четыре метра девяносто пять сантиметров. М-да здесь надо бы не устно решать, а письменно столбиком. Поняла! Оба числа переведу в единые единицы – сантиметры. Ведь в метры восемьдесят шесть или девяносто пять сантиметров не переведёшь – эти величины меньше метра.

Так как в одном метре сто сантиметров, то семнадцать метров восемьдесят шесть сантиметров – это тысяча семьсот восемьдесят шесть сантиметров, а двадцать четыре метра девяносто пять сантиметров – две тысячи четыреста девяносто пять сантиметров. Складываю их столбиком. Получается четыре тысячи двести восемьдесят один. Это столько всего сантиметров. А теперь их надо перевести в метры. Четыре тысячи двести восемьдесят один сантиметр – это сорок два метра восемьдесят один сантиметр. Записываю ответ примера.

В следующем примере надо из пяти тонн ста шестнадцати килограммов вычесть одну тонну девятьсот сорок восемь килограммов.

Как и в предыдущем примере, сначала надо перевести обе величины в единые единицы – килограммы.

А вот теперь я посчитаю, сколько времени у меня уйдёт на решение задач и примеров.

Решение задач займёт три часа двадцать семь минут, а решение примеров три часа сорок шесть минут.

Здесь тоже величины надо перевести в единые единицы – минуты. Для этого количество часов надо умножить на шестьдесят, ведь в одном часе – шестьдесят минут. И к результату прибавить оставшиеся минуты

Три часа двадцать семь минут – это двести семь минут, три часа сорок шесть минут – двести двадцать шесть минут. Складываем двести семь и двести двадцать шесть.

Получается четыреста тридцать три минуты. Чтобы перевести их в часы и минуты, четыреста тридцать три делим на шестьдесят. Получается семь, и тринадцать в остатке. Это семь часов тринадцать минут. Ну, отлично. Я успею всё решить!

Остальные примеры я решу сама – ведь мне уже понятно, как это делать. Надеюсь, и вы поняли тоже. А теперь я предлагаю вам решить одну из моих задач. Я тоже решу, а потом сравним наши решения. Вот эта задача.

На День рождения Матюши я должна прийти вечером в шесть часов сорок пять минут. А уйти мне надо в восемь часов восемнадцать минут того же дня. Сколько времени я проведу у Матюши?

Вы внимательно прочитали условие? А теперь приступаем к решению.

Ну что же, сравним наши решения.

Я надеюсь, вы справились с задачей.

Ну вот, дорогие ребята. Я сейчас постараюсь быстро решить все примеры и задачи, чтобы не опоздать к Матюше. А вы выполняйте свои задания. До свидания, друзья!

Источник