Что обозначает квантор общности

4.2. Кванторы

4.2. Кванторы

Существенное отличие логики предикатов от логики высказываний заключается также в том, что первая вводит количественную характеристику высказываний или, как говорят в логике, квантифицирует их. Уже в традиционной логике суждения классифицировались не только по качеству, но и по количеству, т.е. общие суждения отличались от частных и единичных. Но никакой теории о связи между ними не было. Современная логика рассматривает количественные характеристики высказываний в специальной теории квантификации, которая составляет неотъемлемую часть исчисления предикатов.

Для квантификации (количественной характеристики) высказываний эта теория вводит два основных квантора: квантор общности, который мы будем обозначать символом (х), и квантор существования, обозначаемый символом (Ех). Они ставятся непосредственно перед высказываниями или формулами, к которым относятся. В том случае, когда кванторы имеют более широкую область действия, перед соответствующей формулой ставятся скобки.

Квантор общности показывает, что предикат, обозначенный определенным символом, принадлежит всем объектам данного класса или универсума рассуждения.

Так, суждение: «Все материальные тела обладают массой» можно перевести на символический язык так:

Аналогично этому утверждение о существовании экстрасенсорных явлений можно выразить через квантор существования:

где через х обозначены явления:

С помощью квантора общности можно выражать эмпирические и теоретические законы, обобщения о связи между явлениями, универсальные гипотезы и другие общие высказывания. Например, закон теплового расширения тел символически можно представить в виде формулы:

Квантор существования относится только к определенной части объектов из данного универсума рассуждений. Поэтому, например, он используется для символической записи статистических законов, которые утверждают, что свойство или отношение относится только для характеристики определенной части изучаемых объектов.

Введение кванторов дает возможность прежде всего превращать предикаты в определенные высказывания. Предикаты сами по себе не являются ни истинными, ни ложными. Они становятся таковыми, если вместо переменных либо подставляются конкретные высказывания, либо, если они связываются кванторами, квантифицируются. На этом основании вводится разделение переменных на связанные и свободные.

Свободная переменная не подпадает под действие знаков кванторов, поэтому она характеризует предикат или пропозициональную функцию, а не высказывание.

С помощью комбинации кванторов можно выразить на символическом языке логики достаточно сложные предложения естественного языка. При этом высказывания, где речь идет о существовании объектов, удовлетворяющих определенному условию, вводятся с помощью квантора существования. Например, утверждение о существовании радиоактивных элементов записывается с помощью формулы:

где R обозначает свойство радиоактивности.

Квантор общности используется для высказываний, в которых утверждается, что определенному предикату А удовлетворяет любой объект из области его значений. В науке, как уже говорилось, квантор общности используется для выражения утверждений универсального характера, которые словесно представляются с помощью таких фраз, как «для всякого», «каждый», «всякий», «любой» и т.п. Путем отрицания квантора общности можно выразить общеотрицательные высказывания, которые в естественном языке вводятся словами «никакой», «ни один», «никто» и т.п.

Разумеется, при переводе на символический язык утверждений естественного языка встречаются определенные трудности, но при этом достигается необходимая точность и однозначность выражения мысли. Нельзя, однако, думать, что формальный язык богаче естественного языка, на котором выражаются не просто смысл, но и разные его оттенки. Речь поэтому может идти только о более точном представлении выражений естественного языка как универсального средства выражения мыслей и обмена ими в процессе общения.

Чаще всего кванторы общности и существования встречаются вместе. Например, чтобы выразить символически утверждение: «Для каждого действительного числа х существует такое число у, что х будет меньше у», обозначим предикат «быть меньше» символом

Источник

Предикат

Что такое предикат

Предикат (с латинского praedicatum означает «заявленное, упомянутое, сказанное») — понятие в логике, которым называют утверждение, высказанное о том или ином субъекте. Субъект высказывания — это та вещь или явление, о котором или которой делается утверждение.

Одна из важнейших особенности логики предикатов в том, что все общие имена (такие, как «цветок», «деревня»), знаки свойств («розовый», «большая») и знаки отношений («красивее», «роднее») рассматриваются как относящиеся к одной категории знаков: категории предикаторов (иначе говоря, предметно-истинных функторов).

Предикаторы, в свою очередь, показывают функции, у которых вероятные аргументы — это универсальные в рассмотрении объекты, а значения — истинные оценки. В классической логике они называются «истина» и «ложь». К примеру, возьмем предикатор «человек», который представляет функцию, определяемую как истина каждым отдельным человеком, а каждым отличным от человека существом — как ложь.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Другой пример : функция, которая соответствует предикатору «больше», сопоставляет истину каждой паре объектов или субъектов, один из которых больше. Например, такая пара, как «слон, мышь». Но всем остальным парам, по типу «мышь, слон» и «мышь, мышь», такая функци будет сопоставлять оценку «ложь».

Предикаторы могут быть:

Логические операции над предикатами

Так как предикаты принимают два значения, «истина» и «ложь» (1 и 0), к ним можно применить все операции алгебры логики.

Представим, что в неком множестве N определены два предиката P(x) и Q(x). Рассмотрим все операции с ними по-отдельности.

Область истины в этом случае — объединение областей истинности обоих утверждений.

Область истины здесь — дополнение множества истинности утверждения P(x) до множества N, иначе говоря \(I_overline

=N\I_P=CI_P.\)

Кванторные операции над предикатами

Прежде чем изучить квантовые операции, нужно разобраться, что из себя представляет сам квантор.

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание.

Кванторы впервые были определены немецким математиком Готлобом Фреге. Он упомянул их в своей работе «Begriffsschrift» («Исчисление понятий», 1879 года). Однако сам термин был изобретен английским логиком Чарльзом Пирсом в 1885 году. Вместе со словом «квантор» он ввел также и термин «квантификация», который означает измерение качеств признаков.

Обозначение кванторов

Символическое обозначение кванторов придумал итальянский математик Дж. Пеано в 90-е годы XIX века. Выглядят эти символы так:

\(\forall\) — «для любого», «для каждого», «для всех»;

\(\exists\) — «существует», «найдётся».

! – «единственный»;

: – «такой, что»;

| – «такой, что».

Знак «:» обычно используется в формулировках определений или теорем, которые записываются с помощью кванторов. Знак «|» применяется в определениях множеств.

Виды кванторов

Квантор общности \(\forall\)

Оно истинно только в том случае, когда \(P(x)\) — тождественно истинен. В ином случае данное высказывание ложно.

Оно истинно только в том случае, когда одноместный предикат \(P(x, a_2, …, a_n)\) на множестве \(N_1\) тождественно истинен. В противном случае оно ложно.

Квантор существования \( \exists\)

Примеры применения

Использование предикатов

Использование кванторов

Пусть предикат «x кратно 5». Тогда с помощью квантора общности можно записать ложные высказывания:

В этом случае решение будет выглядеть так:

Чтобы обозначить истинные высказывания, используем квантор существования:

В записи оно будет выглядеть так:

На множестве x простых чисел существует предикат: «Простое число является нечетным». Если мы поставим перед предикатом слово «любое», то получим ложное высказывание «Любое простое число является нечетным». Если мы поставим перед предикатом слово «существует», то получим истинное высказывание «Существует простое число, которое является нечетным».

Так, предикат можно превратить в высказывание, если поставить перед ним квантор.

Источник

MT1102: Линейная алгебра (введение в математику)

В алгебре высказываний применяют логические знаки для записи различных утверждений. Однако нам не достаточно этих знаков для выражения мысли типа «Всякий элемент %%x%% из множества %%D%% обладает свойством %%P(x)%%».

Понятие кванторов

Введем новые логические знаки, обозначаемые %%\forall%%, %%\exists%% и %%\exists!%%. Знак %%\forall%% называется квантором всеобщности, знак %%\exists%% — квантором существования, а %%\exists!%% — квантором существования и единственности.

Пусть %%P(x)%% — одноместный предикат, определенный на множестве %%D%%.

Квантор всеобщности

Используя квантор всеобщности, можно составить следующее высказывание

Читается как: «для любого %%x%% выполняется %%P(x)%%»; «для всякого %%x

P(x)%%»; «для всякого %%x%% верно %%P(x)%%» и т.п.

Пусть %%P(x)%% предикат %%x^2 \geq 0%%, определенный на множестве действительных чисел %%D = \mathbb R %%. Тогда высказывание %%\forall x

P(x)%% имеет вид %%\forall x

x^2 \geq 0%%. Это истинное высказывание, так как для любого значения пременной %%x = a \in \mathbb R %% получаем истинное высказывание %%a^2 \geq 0%%. Однако, высказывание %%\forall x

x^2 > 0%% ложно, например, как при %%x = 0%% получаем ложное высказывание %%0 > 0%%.

Квантор существования

Используя квантор существования, можно составить следующее высказывание

Читается как: «существует %%x%% такой, что %%P(x)%%»; «существует %%x%% с условием %%P(x)%%» и т.п.

Квантор существования и единственности

Используя квантор существования и единственности, можно составить следующее высказывание

Читается как: «существует единственный %%x%% такой, что %%P(x)%%»; «существует единственный %%x%% с условием %%P(x)%%» и т.п.

Отрицание «кванторов»

Докажем первое из них. Пусть высказываине %%\overline<\forall x

P(x)>%% истинно. Тогда высказывание %%\forall x

P(x)%% ложно. Поэтому для некоторого %%x = a%% имеем %%P(a)%% ложно. Тогда %%\overline%% истинно. Итак, для некоторого значения %%x = a

\overline%% истинно. Поэтому высказывание %%\exists x

Аналогично доказывается второе утверждение.

Применение одного из кванторов «понижает» степень предиката на единицу. Из двуместного предиката получается одноместный предикат, а из одноместного — предикат %%0%% степени или высказывание.

Правила перестановки кванторов

P(x,y) \equiv \exists y

P(x,y) \equiv \forall y

Однако, разноименные кванторы переставлять местами нельзя. Рассмотрим двуместный предикат %%P(x, y): x + y = 0%%, определенный на множестве %%\mathbb R%%. Тогда высказывание %%\exists x

x + y = 0%% можно прочитать так: «существует %%x%%, которое в сумме с любым %%y%% равно 0». Это ложно высказывание.

Переставим разноименные кванторы местами и получим высказывание %%\forall y

x+ y = 0%%, которое можно прочитать так: «для любого %%y%% существует %%x%% такой, что их сумма равна 0». Это истинное высказывание. В итоге получили различные истинностные значения высказываний.

Для записи одноименных кванторов существуют следующие сокращения:

\forall y \equiv \forall x, y

\exists y \equiv \exists x, y. \end $$

Источник

Квантор общности

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают квантор всеобщности (обозначение: 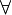, читается: «для всех…», «для любого…» или «любой…») и квантор существования (обозначение: , читается: «существует…» или «найдется…»). В математической логике приписывание квантора к формуле называется связыванием квантора.

Квантор — В логике предикатов, большое значение имеют 2-е операции называемые:

Содержание

Кванторы в естественных языках

Кванторы в математической логике

Вложенные кванторы

Свободные и связанные переменные

Связанное переименование, свободное переименование

Операции над кванторами

Ограниченные кванторы

История появления

Ссылки

Полезное

Смотреть что такое «Квантор общности» в других словарях:

квантор общности — bendrumo kvantorius statusas T sritis automatika atitikmenys: angl. generality quantifier vok. Generalisator, m; Quantor der Allgemeinheit, m rus. квантор общности, m pranc. quantifier universel, m … Automatikos terminų žodynas

Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания

КВАНТОР — логический оператор, с помощью которого высказывание о к. л. отдельном объекте преобразуется в высказывание о совокупности (множестве) таких объектов. В логике используется два основных К.: К. общности, «V», и К. существования, «Э». В… … Философская энциклопедия

Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия

ОБЩНОСТИ КВАНТОР — то же, что всеобщности квантор … Математическая энциклопедия

ЛОГИКА ПРЕДИКАТОВ — центральный раздел логики, в котором изучается субъектно предикатная структура высказывании и истинностные взаимосвязи между ними. Л.п. представляет собой содержательное расширение логики высказываний. В рамках данного раздела любое высказывание… … Философская энциклопедия

Исчисление понятий — «ИСЧИСЛЕНИЕ ПОНЯТИЙ» («Запись в понятиях») сочинение немецкого математика и логика Готтлоба Фреге, положившее начало современной форме математической (символической) логики. Полное название этого сочинения включало указание на то, что в… … Энциклопедия эпистемологии и философии науки

оператор — (от лат. operator действующий) одна из категорий исходных символов искусственного (формализованного) языка, наряду с константой, переменной, связкой и др. категориями. Обычно О. определяется как выражение, связывающее переменные. Примером… … Словарь терминов логики

ПРЕДИКАТОВ ИСЧИСЛЕНИЕ — общее название исчислений математической логики, являющихся формализацией тех разделов совр. логики, к рые изучают субъектно предикатную структуру предложений (высказываний), понимаемую в более широком, чем в традиц. логике, смысле: помимо теории … Философская энциклопедия

Источник

Статья:: Милтон-модель: использование кванторов в речи

Умение говорить неопределённо – один из важнейших навыков коммуникации. И навык этот нужен при создании и поддержании раппорта, и при конструировании метафор, и при речевой интервенции, а так же в большом количестве других случаев.

Когда мы говорим, человек подбирает опыт, подходящий, по его мнению, под описание. Правда это происходит до тех пор, пока он считает, что у него есть соответствие. Чем более неопределённа речь, тем к большему число ситуаций она подходит. Но при этом слишком неопределённая речь может раздражать собеседника, вызывать у него протест.

— Люди ошибаются.
— Да нет, не все ошибаются!

Что произошло? Вполне общая фраза «люди ошибаются» слушателем была интерпретирована как «все люди ошибаются» и вызвала у него протест. Ну, знаете, реклама, политические лозунги, чтение заголовков газет – и к различным сверхобобщениям начинаешь относиться довольно критически. И если слышишь это в речи собеседника – раппорт рвётся.

Аналогичную реакцию может вызывать не только сверхобобщения, но и просто излишне неконкретная речь:

— Встречаются люди, которые почему-то пренебрегают некоторыми нормами.
— Если кто-то кое-где у нас порой честно жить не хочет.

Соответственно, при построении фраз желательно уметь контролировать уровень неконкретности и не создавать неопределённости сверх необходимого. Те есть говорить с оптимально подходящим уровнем (не)конкретности.

Кванторы

Квантор (от лат. quantum — сколько), логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа «все», «каждый», «некоторый», «существует», «имеется», «любой», «всякий», «единственный», «несколько», «бесконечно много», «конечное число», а также все количественные числительные.

В моделях языка, используемых в НЛП (мета и Милтон- моделях), рассматривается только квантор всеобщности. Я хочу показать, что использование других кванторов, в особенности кванторов существования, может дать дополнительные инструменты и расширить возможности речевого воздействия человека, практикующего НЛП или Эриксоновский гипноз.

Когда мы начинаем говорить о множестве предметов или действий, кванторы необходимы для понимания того, относится ли высказывание ко всему множеству или только к его части. Например, если мы говорим «люди», можно интерпретировать высказывание и как «все люди», и как «некоторые люди». Аналогично с глаголами: «ошибаются» можно интерпретировать и как «во всём ошибаются», и как «хоть в чём-то ошибаются», и как «постоянно ошибаются», и как «иногда ошибаются».

Кванторы всеобщности

Кванторы общности в речи создают определённые ограничения, так как утверждают, что «правило исключений не имеет». В языке они выражаются словами: все, всегда, постоянно, каждый, никто, ничто, никогда и т.п.
— Все выступавшие смеялись.
— Никто не обращал на него внимания.
— Она постоянно удивляется.
— Иван Петрович никогда не опаздывал.
При этом квантор общности может принимать значение как значение «для всех/всего»: всё, все, всегда, вечно, везде; так и значение «ни для кого/чего»: никогда, нигде, никто, ничего.

Кванторы существования

Кванторы существования сообщают что «множество не пустое», что какое-то явление или вещь существует, при этом придавая речи оттенок неопределённости. В речи будут выражаться словами: кое-кто, кое-что, какой-то, несколько, некоторый, иногда, однажды, бывает, случается и т.д.

— У нас что-то произошло.
— У кого-то нет еды.
— Мужчины бывают непоследовательны.
— Иногда Иванов заходил к соседу сверху.

С грамматической точки зрения, кванторы существования могут быть выражены:

местоимением: кто-то, что-то, какой-то, чей-то, кое-кто, кое-что, кое-какой, что-либо;
глаголом: бывает, случается, происходит;
наречием: изредка, иногда;
прилагательным:редкий, возможный, вероятный;
числительным: одни, много, немного, мало, немало, несколько;
причастием:случающийся, происходящий, бывающий.

Как вы видите, кванторов существования в речи намного больше, чем кванторов общности.

Количественные числительные

Количественные числительные просто сообщают о точном размере множества или его части. В неконкретной речи используются мало.

Один, оба, трое, пять, половина, две трети.

Виды неопределённости

Для субъекта (подлежащего) неопределённость касается как «размера доли», которую квантор описывает, так и точности её определения.

— Мужчины думают о семье.
— Некоторые мужчины думают о семье.
— Большинство мужчин думают о семье.
— Какие-то мужчины думают о семье.

Аналогично для объекта (дополнения):

— Мужчины думают о семье.
— Мужчины думают хоть о какой семье.
— Мужчины думают о всей семье.
— Мужчины думают о чьей-то семье.

Для предиката (сказуемого) неопределённость существует практически всегда и касается: продолжительности, частоты использования, места, причины и т.д.

— Мужчины думают о семье.
— Мужчины хотя-бы изредка думают о семье.
— Мужчины постоянно думают о семье.
— Мужчины где-то думают о семье.
— Мужчины зачем-то думают о семье.

Увеличение неопределённости

Посмотрим, как растёт неопределённость при использовании кванторов.

Кванторы всеобщности

Сообщают об отсутствии исключений – либо «всё», либо «ничего». Соответственно, ни о какой неопределённости речи идти не может. И именно это часто вызывает протесты и желание проверить: а действительно ли исключений нет.

— Все сотрудники….
— Ни одна из компаний…

Количественный числительные

Довольно конкретны, но они сообщают, например, о размере части, но не о том, кто или что конкретно в эту часть входит. Так что могут быть варианты.

— Половина сотрудников против.
— Две трети компаний испытывают недостаток наличности.

Кванторы существования

Ещё более неопределённы – неизвестно не только что входит в «дольку», но и точные размеры этой «дольки».

— Некоторые сотрудники…
— Большинство компаний…

К тому же внутри кванторов существования тоже можно провести деление. Например, слова редко, часто, многие, большинство, несколько более конкретны чем изредка, кое-кто, кое-где, случается.

Отсутствие квантора

— Сотрудники против.
— Компании испытывают недостаток в наличности.

Замещение смысловых слов

Кванторы могут замещать смысловые слова:

— Все люди работают.
— Все работают.

— Многие рабочие были против.
— Многие были против.

При этом неопределённость растёт, так как непонятно, к какому конкретно множеству относится квантор. Например последняя фраза, даже в определённом контексте, может обозначать и «многие рабочие», и «многие рабочие и их родственники», и «руководство завода», и «большая часть населения города» и т.д.

Правда здесь неопределённость увеличивается относительно уровня неопределённости, задаваемой самим квантором.

Использование

Размер доли

никто
нигде
ничего
пусто

кое-где кое-кто изредка мало немного меньшинство меньшая часть одна восьмая	бывает случается иногда некоторые половина	часто регулярно большинство большая часть две трети много	все всё всегда вечно постоянно целиком

Аккуратное использование «размером» во многих случаях будет весьма полезным. Например, если вы хотите повысить авторитетность высказывания, желательно сообщить о большой доле:

— Большинство физиков с этим согласно.
— Я постоянно оцениваю ситуацию на рынке.

При этом желательно очень аккуратно залезать в крайности, то есть использовать кванторы всеобщности. Фраза: «все психологи это знают», вместо «большая часть психологов это знает» может быть воспринята «в штыки». Но в то же время, если есть возможность сослаться на «всех», фраза будет звучать более внушительно.

— Все члены руководства хотят изменит ситуацию.
— Мы всегда правильно оформляем бумаги.

В то же время, если вы хотите указать на редкость случая, размер доли желательно уменьшить:

— Изредка приходится пересматривать ситуацию.
— Все мы иногда ошибаемся.
— Никто из нас не хочет тебе плохого.

— Случается, что люди обижаются.
— Некоторые компании пытаются договориться полюбовно.

Создание трюизмов

Кванторы можно эффективно использовать для конструирования трюизмов – (как бы) совершенно истинных утверждений:

— Женщины бывают болтливы.
— Сейчас где-то кто-то что-то ест.
— Иногда очень хочется бросить всё.

При этом нам надо создать выражение, которое бы полностью соответствовало карте Клиента и не создавало бы у него возражений. В большинстве случаев слишком точные выражения, за исключением общеизвестных фактов, не слишком подходят. То есть кванторы всеобщности и количественные числительные годятся только для проверяемых ситуаций.

— Вы все сидите. (Действительно, в помещении никто не стоит).
— На столе два карандаша. (Если их действительно два).

Так что кванторы всеобщности и количественные числительные в трюизмах удобнее всего использовать с кванторами существования.

— Почти половина человечества – мужчины.
— В жизни каждой женщины когда-нибудь наступает момент, когда она готова взорваться.

Так же нужно с осторожностью относиться к отсутствию кванторов, так как наиболее частая интерпретация – это как раз квантор всеобщности. Например, в ответ на фразу: «Женщины обидчивы», можно услышать: «Ну не все же!»

В результате, наиболее часто используемый инструмент – это кванторы существования.

— Редкая птица долетит до середины Днепра.
— В некоторых ситуация разобраться трудно.
— Случается, что люди понимают вас неправильно.

Теперь по поводу использования трюизмов.

Установление и поддержание раппорта.

Если вы говорите о чём-то, полностью соответствующим действительности, вы скорее всего точно попадаете в карту собеседника.

— Большинство компаний в конце концов разоряются.
— Некоторые пишут полную ерунду.
— Иногда бывает трудно с собой справиться.

Создание определённой рамки восприятия.

— Мы хоть иногда задумываемся о вечном.

Эта фраза позволяет сдвинуть фокус внимания на «вечное» и подготавливает к разговору на эту тему. Если Клиент очень переживает из-за своих действий, то речь можно начать с фразы:

— Все люди хоть иногда ошибаются.

Эта фраза предполагает, что даже вполне успешные люди могут ошибаться, и Клиент может быть успешен даже если он сделал что-то «не то».

Для большей уверенности в собственных силах, Клиенту можно сказать:

— Мы можем справиться практически с любой проблемой, если приложим усилия.

На одну и ту же ситуацию можно иметь несколько противоположных, но при этом совершенно истинных, взгляда.

— Женщины бывают крайне раздражительны.
— Встречаются очень уравновешенные женщины.

Так что всё зависит от вашей цели.

Разрушение ограничивающих убеждений

Кванторы всеобщности довольно часто встречаются в ограничивающих убеждениях:

— Меня никто не любит.
— Мужчины постоянно обманывают.
— Всё хорошее когда-нибудь кончается.

Для разрушения такого убеждения нужно каким-то образом повысить неопределённость утверждения, что создаст дополнительные выборы.

Добавление квантора существования.

Например, к кванторам общности можно добавить кванторы существования и получиться «общее правило, но не для всех».

— Всегда существует опасность.
— Всегда где-то для кого-то существует опасность, но даже это не обязательно.
— Всех обманывают.
— Да, ты прав. Всехиногда обманывают.

Обратите внимание, что в последнем варианте квантор всеобщности является субъектом, а квантор существования относится к предикату. Собственно, на этом можно и играть, – так как неопределённость повышается при добавлении квантора существования к любой части сообщения.

Замена квантора всеобщности на квантор существования.

— Люди всегда ошибаются.
— Да, все изредка ошибаются.

Соответственно, если в ограничивающем убеждении отсутствуют кванторы, и, судя по всему, отсутствие трактуется как квантор общности – один из простых способов, это просто добавить квантор существования.

— [Все] мужчины непостоянны.
— На самом деле только некоторые мужчины непостоянны.

Создание замешательства.

Ещё один способ использования кванторов – создание замешательства. Совмещая различные типы кванторов или используя их грамматически или логически не совсем правильно, мы можем создать парадоксальные фразы (речевые парадоксы).

— всё и ничего;
— редко, но постоянно;
— две трети, то есть половина;
— постоянно изредка случается.

— Вы меня ненавидите.
— Некоторые из нас двоих всегда относятся к тебе хорошо.

— Мужчины постоянно обманывают.
— Мужчины обманывают постоянно, но крайне редко.

— Меня никто не любит.
— Большая часть никого о тебе даже не знает.

— Он всегда меня обманывает.
— Случается, что он всегда тебя обманывает?

Источник