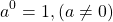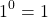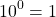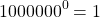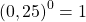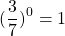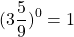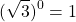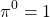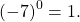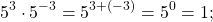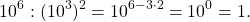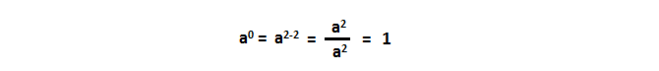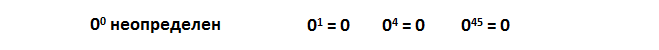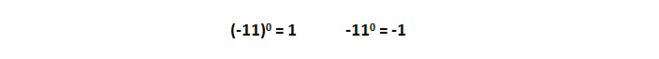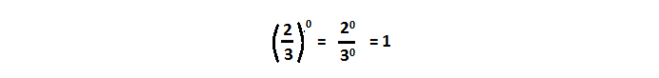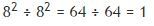Что обозначает нулевая степень
Степень 0
В алгебре возведение с нулевую степень встречается часто. Что такое степень 0? Какие числа можно возводить в нулевую степень, а какие — нет?
Любое число в нулевой степени, за исключением нуля, равно единице:
Таким образом, какое бы число ни возвели в степень 0, результат всегда получится одинаковый — единица.
И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.
Единственное исключение — нуль.
Нуль в нулевой степени не определен, такое выражение не имеет смысла.
То есть в нулевую степень можно возводить любое число, кроме нуля.
Если при упрощении выражения со степенями получается число в нулевой степени, его можно заменить единицей:
Если при упрощении получается переменная или выражение с переменными в нулевой степени, пишем дополнительное условие — основание степени должно быть отличным от нуля:
Better Explained: Как понять ноль в нулевой степени?
Как мы можем повторить ноль нулевое количество раз и получить единицу? Всё дело в том, что наш подход к степени числа как к многократному умножению неверен. Нам нужно сменить парадигму. Давайте посмотрим, как мы привыкли воспринимать арифметические действия, и что они на самом деле из себя представляют.
Сложение
Как мы привыкли думать: это повторяющийся счёт
Как на самом деле: перемещение
Умножение
Как мы привыкли думать: это многократное сложение
Как на самом деле: масштабирование
Степень
Как мы привыкли думать: многократное умножение
Как на самом деле: рост с течением времени
Смотрим на арифметику как на преобразование
Отойдём на шаг назад. Как мы изучаем арифметику? Нас учат, что числа — это некое количество единиц; сложение — это прибавление одного количества единиц к другому количеству единиц (3+4 = 7), а умножение — это многократное сложение (2*3 = 2+2+2 = 6).
Очевидно, что эта модель восприятия неполноценна. Числа — это не просто единицы чего-то; гораздо лучше представлять их как некие точки с определённым положением на линии. Положение может быть отрицательным (-1), либо между другими числами (2²), либо в другом измерении (i).
Таким образом арифметика предстаёт перед нами как способ преобразовывать число. Сложение становится перемещением (+3 — это перемещение на 3 единицы вправо); умножение становится масштабированием (*3 — это увеличить число в три раза).
А что же такое тогда степень числа?
Познакомьтесь с Экпандотроном™
Это Экспандотрон 3000. Он выглядит как достаточно потрёпанная микроволновка, но вместо подогрева пищи она занимается ростом чисел. Просто положите число внутрь и проделайте несколько простых операций.
Вуаля! После звукового сигнала достаём наше новенькое готовое число. Например, мы хотим изменить 1 на 9. Что нам нужно сделать?
Что мы видим? Мы видим, как число начинает преобразовываться: 1; 1,1; 1,2. По окончании первой секунды оно уже выглядит как 3 и продолжает меняться: 3,1; 3,5; 4,0; 6,0; 7,5. И по окончании второй секунды оно превратилось в 9.
В математическом представлении Экспандотрон (или показательная функция) делает для нас следующее:
Например, 3 2 = 9/1. Основанием является то количество раз, в которое нам нужно вырастить число (х3), а степенью — количество времени (2). Формула типа 2 n означает «Используйте свой Экспандотрон на мощности х2 в течение n секунд».
Работу Экспандотрона мы всегда начинаем с 1, чтобы посмотреть, как он меняет одну единицу. Если мы хотим посмотреть, что случится с 3 в Экспандотроне, мы просто масштабируем конечный результат. Например:
Начните с 1 и умножьте на двойку в третьей степени: 1*2 3 = 1 * 2 * 2 * 2 = 8
Начните с 3 и умножьте на двойку в третьей степени: 3*2 3 = 3 * 2 * 2 * 2 = 24
Каждый раз, когда вы видите простую степень, вы начинаете с 1.
Идём к пониманию масштабирующего множителя
При умножении мы можем просто указать конечный масштабирующий множитель. Хотите число в 8 раз больше? Умножаем на 8. Готово.
Степени более капризны в обращении. Вот как они работают:
Вы: Хочу вырастить вот это число.
Экспандотрон: Ок, давай его сюда.
Вы: И насколько большим оно станет?
Экспандотрон: Пффф, без понятия. Давай посмотрим.
Вы: Посмотрим? Я думал, ты зна.
Экспандотрон: Тихо! Оно растёт! Растёт!
Экспандотрон: Готово! Это шедевр!
Это может звучать раздражающе неопределённо, но знаете, что? Большинство явлений природы заканчиваются неизвестно чем!
Как думаете, бактерия действительно планирует делиться каждые 14 часов? Нет, она просто питается забытым вами в холодильнике хлебом и растёт так быстро, как только может. Чтобы предсказать поведение этой бактерии, мы можем лишь использовать значения темпа её роста и длительности роста — и только потом мы получим конечное значение.
Иными словами, степень числа — это такой способ сказать «Начинаем с таких условий, изменяем их и смотрим, к чему мы придём». Этим и занимается наш Экспандотрон.
Идём к пониманию дробных степеней
Очень легко запутаться, если мы думаем о двойке в полуторной степени привычным способом — как о многократном умножении. Но в Экспандотроне всё просто: 1,5 — это всего лишь проведённое в нём время.
2 1,5 означает 1,5 секунды в машине, значит, этот рост окажется где-то между двукратным и четырёхкратным.
Умножение степеней
Что если мы захотим прогнать два цикла роста один за другим? Ну, например, мы используем машину в течение 2 секунд, а потом ещё 3 секунды на той же мощности:
Представьте самую обычную микроволновку. Разве это не будет самый обычный цикл длительностью в 5 секунд? Будет. Здесь происходит то же самое — раз уже мощность (основание) остаётся одинаковой, мы просто складываем время:
Квадратные корни
Продолжим. Предположим, мы выбрали мощность а и устанавливаем рост в течение 3 секунд:
Неплохо. Как будет выглядеть рост в течение половины этого времени? Логично, что 1,5 секунды.
А если мы проделаем то же самое два раза?
частичный рост * частичный рост = полный рост
Смотрим на это уравнение и видим, что «частичный рост» — это квадратный корень из значения полного роста. А если мы разделим время на три части?
частичный рост * частичный рост * частичный рост = полный рост
А вот и кубический корень! Это даёт нам интуитивное понимание того, почему деление степеней даёт нам корни: мы разбиваем время на равные доли.
Отрицательные степени
А как быть с отрицательными степенями? Отрицательные степени для нас будут значить обратный отсчёт во времени. Если движение вперёд во времени приводит нас к росту, движение назад, скорее всего, выльется в уменьшение числа.
Это значит следующее: «Секунду назад у нас была половина от текущего количества (1/2 1 ). Любой график экспоненциального роста строится именно так.
Выберите точку на шкале времени, например, 3,5 секунды (2 3,5 = 11,3). Через секунду мы удвоим наше количество (2 4,5 = 22,5). А секунду назад у нас была всего лишь половина от текущего количества (2 2,5 = 5,65).
Приходим к нулевой степени
Значит, масштабирующий множитель равен единице, значит, никаких изменений с нашим числом не происходит. Новое число будет равняться исходному числу, то есть (вы же помните, что исходное число у нас единица?) единице. Масштабирования не происходит.
Приходим к нулевому основанию
Приходим к нулевому основанию в нулевой степени
0 в степени 0 означает рост х0 в течение 0 секунд. Хоть мы и планировали аннулировать число, мы так и не запустили машину. Новое число равно исходному числу (то есть в наш Экспандотрон мы положили единицу), масштабирующий множитель тоже равен единице.
Конечно, Экспандотрона на самом деле не существует (а жаль!). Конечно, числа на самом деле не выстраиваются в линейку — они всего лишь один из множества способов взглянуть на мир.
По материалам очаровательной статьи на Better Explained.
«А сколько будет 0 в степени 0?» или прощай мозг.
неопределенность, нельзя так делать, как на ноль делить нельзя))
В общем, либо получится 1 (как любое число в нулевой степени), либо вообще недопустимая операция (как 0 в неположительной степени), но точно не 0))
В программировании существует переменная, хранящая результат.
Допустим, вот псевдокод топорного умножения:
Функция_УМНОЖИТЬ(Множимое M, Множитель N)
Здесь переменная ИТОГО изначально равна НУЛЮ, так как будет копить Множимое N-раз через сложение.
А вот функцию возведения в степень аналогична, но немного иная:
Функция_ВОЗВЕСТИ(Основание степени M, Показатель степени N)
Тем самым, переменная ИТОГО изначально не должна равняться НУЛЮ, так как будет копить Основание N-раз через умножение.
Более простым языком: Допустим, имеем уравнение Z=0^Y*X. Если Y равен 1, мы умножаем X на 1 НОЛЬ. Т.е. сокращённая запись принимает вид Z=0*X. Если же Y равен 0, мы не умножаем X ни на что вообще. Т.к. сокращённая запись уже имеет вид Z=X, где нет место НУЛЮ, тем самым, формула включает в себя 0 НОЛЕЙ.
вот почему https://www.youtube.com/watch?v=r0_mi8ngNnM
Любое число в нулевой степени, за исключением нуля, равно единице, гугл.
Сколько будет 0-2=? Если от этой цифры нельзя нечего взять
все визуально просто: постройте график функции, приближаясь все ближе к нулю, сами увидите, что «0» в нулевой степени остановится на точке «1»(плсмотрите ролик Физика Побединского в ютубе «0» в степени «0»)
Думаю примера будет достаточно:
2 ^ 0 = 1 = 1
2 ^ 1 = 1 * 2 = 2
2 ^ 2 = 1 * 2 * 2 = 4
2 ^ 3 = 1 * 2 * 2 * 2 = 8
Нашёл дневник
Ответ на пост «На одной волне»
Подержите мое пиво! ))) Бродил как то в Тюмени по торговому центру и забрел в магазинчик «Экспедиция». и прикупил понравившуюся мне прикольную футболку с прикольным рисунком «медведь гонится за человеком» и надписью «Siberian fast food». Возвращаюсь из командировки, жду трансфер в аэропорту Бомако (Конго). и тут ко мне подходит паренек в футболке с АБСОЛЮТНО (до мелочей) ТАКИМ ЖЕ РИСУНКОМ, но с надписью «Canadian fast food»! Парень, конечно же из Канады, но, как позже оказалось, его дедушка с бабушкой были русские эмигранты и он очень обрадовался узнав. что я из России и даже попытался говорить на русском.
Бывший.
Был друг, хороший человек. Попал в блуду, попросил денег. Я взял кредит. Друг выплыл, отдал три четверти, больше у него нет. (около сотыги еще должен, плачу)
Была жена. Случилась беда, онкология. Метания туда-сюда, беготня. Врачи, больница, взял кредит. Слава богу, полная ремиссия и жена мне говорит, что жила как-то скучно, (или не так), в общем ей не хватает нового и и свежего.
Я не новый, явно не свежий, (47Лет)
Около миллиона еще должен.
На одной волне
Лечу домой на праздники в таком прикиде, чтобы удивить семью. Перед вылетом встретил в аэропорту этого незнакомца. Сразу скорешились.
Петербуржцы
Как-то так
«В меню писать надо постоянно котлеты, но это не значит, что их нужно давать»
Ростовский депутат просил подчиненных сэкономить на еде для детей, но попал на видео
Депутата подозревают в хищении бюджетных денег для детского отдыха. Латышев руководит несколькими лагерями: ООО ДОК «Солнечная Поляна», ООО Пансионат «Орленок», ООО Пансионат «Дмитриадовский». Накануне в лагеря приходили с обысками.
Предполагается, Латышев на видео подсчитывает с подчиненной сэкономленные на детском питании деньги.
— Наталья сказала котлеты все время давать, а Оля говорит — мы же тогда будем все дороже… Как нам быть? — говорит на видео женщина.
— Нет, она говорит, в меню писать надо постоянно котлеты, но это не значит, что их нужно давать, — отвечает своей подчиненной Виталий Латышев.
Женщина предлагает выйти из ситуации, чтобы не попасться «проверяющим инстанциям».
— Если даже писать 90 рублей, а в другой день, когда приедет проверка, 130 рублей, то 3700. Трешка сэкономится, — утверждает собеседница.
После подсчетов на калькуляторе он резюмирует, что 5 рублей экономит полтора миллиона, женщина соглашается и говорит, что 10 рублей экономит три миллиона.
— Я почему хотела… пусть пока девочки не заняты, посчитают. В тот день, когда инстанции приезжают, пусть по нормам дают. Но в другие дни, когда инстанций нет, там же не по нормам все дается, крупы, мясо, все. Может им какой-то пирожок дешевый давать, дети голодными не будут и не будут звонить родителям, — добавляет женщина.
Сейчас следствие проверяет чиновника на причастность к воровству денег, выделяемых на отдых детей из малообеспеченных семей. С 2015 года местные власти выделили на это около миллиарда рублей. По одной из версий следствия, около 30% из этой суммы могло осесть у Латышева.
Число в нулевой степени
Возведение в степень является одним из основных математических действий, без которых невозможны сложные расчеты. При этом отдельного рассмотрения заслуживает нулевая степень числа.
Возведение числа в нулевую степень
Известно, что при x 0 любое x равно 1 (x 0 = 1). Чтобы доказать это, нужно выяснить, откуда собственно взялся этот ноль?
Для этого вспомним формулы сложения и вычитания степеней.
7 3 = 7 2+1 = 7 2 × 7 1 = 7 × 7 × 7, ⇒
7 0 = 7 3-3 = 7 3 ÷ 7 3 = 1
Доказательство получено. Однако есть исключение из этого правила.
Парадокс нуля
Здесь все гораздо сложнее, но не настолько, чтобы не разобраться.
Известно, что 0 x = 0. Например: 0 4 = 0 × 0 × 0 × 0 = 0
Почему же мы часто встречаем выражение 0 0 = 1?
Подберем значения по табл.1.
Таблица 1. Функция ƒ(x) = x x
| x | x x |
| 1 | 1 |
| 0,9 | 0,909 |
| 0,8 | 0,836 |
| 0,7 | 0,779 |
| 0,6 | 0,736 |
| 0,5 | 0,707 |
| 0,4 | 0,693 |
| 0,3 | 0,697 |
| 0,2 | 0,725 |
| 0,1 | 0,794 |
| 0,01 | 0,955 |
| 0,001 | 0,993 |
Как видим, с определенного момента значение x x растет вместе с уменьшением x. В этом нет ничего сверхъестественного, это всего лишь пример действия формулы
Изобразим это на графике

Таким образом, делаем предположение, что это выражение является пределом.
Выразить это можно так:
Проверим, вычислив это значение.
Преобразуем основание выражения. Получаем:
x x = (e ln x ) x = e x ln x
Получаем следующее выражение:
Пользуемся правилом Лопиталя:
Официальная позиция современной математики гласит, что выражение 0 0 — представляет собой неопределенность, то есть не имеет точного значения.
Однако на практике, при расчетах, его значение подстраивается под конкретные требования. И чаще всего в этих случаях оно равно единице. Чтобы лучше разобраться с темой нулевой степени, советуем посмотреть видео ниже.
Чему равно число в нулевой степени?
Доброго времени суток.
Так, если у нас есть 2 в квадрате, то мы 2 умножаем на 2 и получаем 4; если 2 в кубе, то 2 умножаем на 2 и потом еще раз на два и получаем 8 и тд.
А вот в случае с нулевой степенью мы не умножаем, а наоборот делим число на само число. Соответственно, результатом этого действия будет единица.
Любое число в нулевой степени равно единице, потому что x^y/x^y = 1, а при делении, степени чисел вычитаются и степень, в данном случае, получается равной нулю.
Курс начальной школы.
Из основных свойств нуля: при возведении любого числа в нулевую степень получаем 1.
Из свойств степеней:
если n=m=1, то уровень наглядности повышается.
Нулевая степень числа равна единице за исключением ноля.Это становится очень хорошо понятно, если посмотреть на следующий пример:
Любое отрицательное число при возведении в нулевую степень равно 1, но если минус стоит просто перед числом, тогда минус 1.
Любая дробь в нулевой степени равна 1, ведь ее всегда можно записать в виде, где числитель и знаменатель будут в нулевой степени.
Какое бы число вы не пожелали возвести в нулевую степень результат будет равным единице. А если, к примеру говорить о возведении самого нуля, то в данном случае в какую бы степень вы не возводили ноль, значение всегда будет равно тому самому возводимому нулю.
Попробуем привести несколько примеров, чтобы наглядно увидеть решение:
Но это еще можно назвать сложным объяснением, так как самое легкое встречается как раз в школьном учебнике и проще наверно и не придумать
Поэтому видимо и запомнили навсегда, что число в нулевой степени равно единице.
Это несложное задание со школьных времён довольно просто запомнить каждому школьнику. Помню, что учительница говорила на эту тему нам в те времена. Если возводите какое бы то ни было числов нулевую степень в нулевую степень, то оно всегда будет иметь рсвоим итоговым результатом единицу. Ответ: единица.
Чтобы выделить все числа из определённого диапазона по условию необходимо:
В данном неоднозначном вопросе отметился даже Коши и Бурбаки..
Но попробуем произвести своё доказательство..
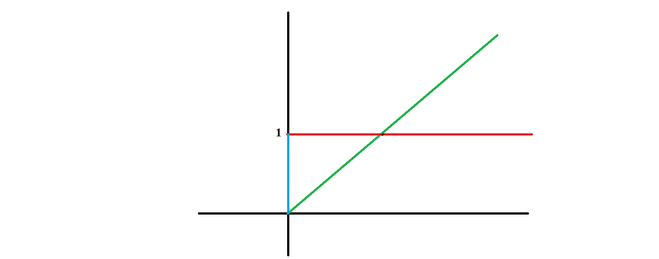
Если рассмотреть ряд степенных функций в первом квандранте, всё время увеличивая степень, то такая функция будет вырождаться в ступенчатую функцию..
При этом скачок будет равен 1..
На протяжении от нуля до единицы будет область начала скачка, т.е. координаты аргументов могут быть произвольными, тогда как функция будет равна 1.. Налицо будет неопределённость..
Теперь рассмотрим функции корней, что являются функциями в отрицательной степени, устремляя их показатель в бесконечность также приходим к скачкообразной функции, пр
На рисунке красным обозначена предельная функция, в области фронта скачка (обозначено синим) имеется неопределённость..
Есть еще такое объяснение
По этому правилу можно найти любой факториал, кроме (-1)!, потому что получится
И поэтому факториалы от любых целых отрицательных чисел не определены.
А вот факториалы от нецелых чисел вполне определены, и означают как раз гамма-функцию, описанную Грустным Роджером.
Для целых х будет Г(x) = (x-1)!
А для нецелых х будет Г(x) = ʃ(0,oo) e^(-t) * t^(x-1) dt
Обрати внимание, что интеграл берется по переменной t, а функция зависит от х, который находится в показателе степени.
Такие дроби называются ОБРАТНЫМИ. В произведении они дают единицу.