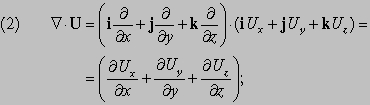Что обозначает вектор в физике

Что такое векторные величины в физике? Все векторные величины

Содержание:

Физические величины служат для численного выражения различных характеристик материальных предметов и физических явлений. Все физические величины разделены на два вида. Векторные величины в физике – это те, которые кроме численного выражения обязательно характеризуются направлением. А вот обычные величины называют скалярными. Примерами таких величин могут служить:

Что такое векторная величина

Векторные величины в физике, список которых приведен ниже, широко известны:

Чтобы досконально разобраться в их смысле, попробуем рассмотреть простой пример. Каждый из нас неоднократно бросал или подбрасывал какой-либо предмет. Пусть это будет теннисный мячик. Сделать это можно разными способами:

В нашем эксперименте будем предполагать, что все три раза мячик бросает один и тот же человек, а сила броска всегда примерно одинакова. Какие результаты будут в итоге? Догадаться довольно просто: в каждом из случаев результат будет разным, потому что три раза мячик бросали в разном направлении. Таким образом мы увидели, что векторная величина это в физике одновременно две характеристики какого-либо физического процесса или состояния.

Действия над векторными величинами

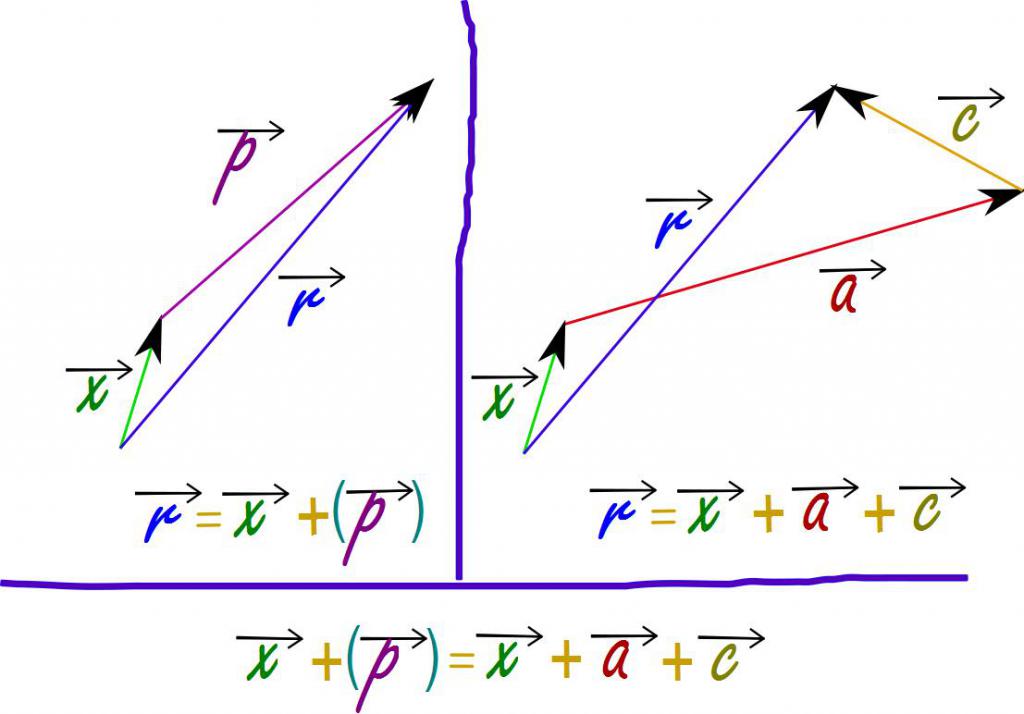
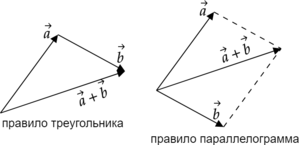
Теперь, когда мы установили, что такое векторная величина в физике, настало время подумать о действиях над такими величинами. Их можно складывать, вычитать, умножать, но важно помнить, что определяющим фактором будет их направление. Действия над такими величинами производят с использованием правил, принятых в математике. Например, сложение векторов производят с использованием правил треугольника или параллелограмма.

Что значит векторная величина в обычной жизни

В повседневной жизни мы зачастую даже не задумываемся, что значит векторная величина, и не замечем, что пользуемся векторами. Допустим, что два друга собрались поехать на рыбалку и договорились о встрече с утра за 100 м от автобусной остановки. Согласитесь, что намеченное мероприятие может оказаться под угрозой из-за того, что не было указано в каком конкретно направлении от остановки следует двигаться на указанное расстояние.

Другой пример из всем известной басни. Речь про лебедя, рака и щуку, которые дружно собрались потянуть тяжелый воз. Тяговую силу каждый из них приложил в своем направлении, не согласовав его с другими. В итоге воз не тронулся с места. Говоря языком физики, все векторные величины силы математически сложились так, что их равнодействующая оказалась равной нулю.

Ну и в заключительной части вспомним о том, что векторы в виде указующих стрелок принято использовать на дорожных знаках и различных табличках, информирующих о направлении движения в непредвиденных ситуациях либо помогающих найти соответствующий объект.

Источник

ВЕКТОР

Полезное

Смотреть что такое «ВЕКТОР» в других словарях:

Вектор — Вектор многозначный термин; величина, характеризующаяся размером и направлением. В Викисловаре есть статья «вектор» … Википедия

Вектор — Вектор. Проекции x, y, z вектора OM на оси i, j, k. ВЕКТОР (от латинского vector, буквально несущий), отрезок прямой определенной длины и направления. С помощью вектора изображают так называемые векторные величины: силу, скорость, ускорение.… … Иллюстрированный энциклопедический словарь

ВЕКТОР — (от латинского vector, буквально несущий), отрезок прямой определенной длины и направления. С помощью вектора изображают так называемые векторные величины: силу, скорость, ускорение. Обычно вектор обозначается буквой жирного шрифта a или OM… … Современная энциклопедия

вектор — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=5044] вектор Упорядоченный набор из некоторого количества независимых действительных чисел (таково одно из многих определений — то, которое принято в экономико математических… … Справочник технического переводчика

Вектор — [vector] упорядоченный набор из некоторого количества независимых действительных чисел (таково одно из многих определений то, которое принято в экономико математических методах). Например, суточный план цеха может быть записан 4 мерным вектором… … Экономико-математический словарь

ВЕКТОР — ВЕКТОР, в математике величина, имеющая как размер, так и направление, в противоположность СКАЛЯРУ, имеющему только размер. Например, СКОРОСТЬ объекта определяется численным значением скорости и направлением, в котором он движется в данный момент … Научно-технический энциклопедический словарь

ВЕКТОР — (vector) Краткое обозначение перечня переменных, которые могут сами по себе быть числами или алгебраическими выражениями. Вектор может быть записан как строка, так что х=(х1, х2. хN), или как столбец, так что Говорят, что вектор с N элементами … Экономический словарь

ВЕКТОР — в молекулярной генетике самостоятельно реплицирующаяся молекула ДНК, способная включать чужеродную ДНК (гены) и переносить ее в клетки, наследственные свойства которых желают изменить. Обычно вектор создают на основе ДНК плазмид и вирусов (в т. ч … Большой Энциклопедический словарь

ВЕКТОР — В механике: такие количества, которым приписывается не только величина, но и направление, как скорость, сила и т. п. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. вектор (лат. vector везущий, несущий) мат,… … Словарь иностранных слов русского языка

вектор — а, м. vecteur m. спец. Отрезок прямой, характеризующийся численным значением и определенной направленностью. БАС 2. Отм. в Татищев 1816 в словосочетании радиус вектор. Вектор. Битнер 1905. ЭС. Лекс. Уш. 1935: ве/ктор, ве/кторный … Исторический словарь галлицизмов русского языка

ВЕКТОР — (от лат. vector несущий) отрезок определенной длины и направления. Обычно вектор обозначается буквой a или (первая буква начало, вторая конец отрезка); абсолютная величина (длина) вектора записывается … Большой Энциклопедический словарь

Источник

Что такое вектор и векторные величины? Какие их свойства, признаки?

Содержание:

Одни величины в физике называют скалярными, другие – векторными, и последним посвящён целый раздел алгебры. Кратко разберёмся, какие величины называют векторными, определим их свойства. Узнаем основные параметры этих отрезков, сферы применения, возможные манипуляции с ними.

Что такое векторная величина

Часто линия и сторона действия объединяются в направление вектора.

Очевидно, термин происходит из латинского языка: vector – несущий.

Обозначение

В последней ситуации первая буква указывает на начальную точку или начало направленного отрезка, вторая – на его конец. Их порядок указывает на направленность вектора. Отсюда следует, что порядок указания букв важен. AB ≠ BA как в случае с обычными отрезками. На чертежах направление изображают стрелкой на конце, начало представляют точкой. Длиной называется разница между конечной и начальной точками. Обозначается преимущественно буквой V со стрелкой/риской вверху \overrightarrow .

Свойства и классификация векторов

Величины можно складывать – суммировать, отнимать – вычислять их разницу, умножать – находить произведение и определять длину (модуль). Причем операции производятся как с векторами, так и по отношению к направленному отрезку и числу.

Применение

Применение направленных отрезков упрощает определение меры углов между отрезками, лучами, прямыми, вычисление площадей геометрических фигур. В компьютерной графике векторы-нормали применяют для освещения сцен и создания масштабируемых изображений, качество которых не страдает при уменьшении или увеличении картинки. Рассматриваемые отрезки положены в основу системы полярных координат. Существует отдельный раздел компьютерной графики – векторный.

Скользящие «несущие» широко применяются в физике (механике), например, это сила. При перемещении вектора силы вдоль прямой, которой тот принадлежит, момент силы остаётся константой. При перемещении на иную прямую он зачастую меняется. Сила не рассматривается как свободный направленный отрезок.

Источник

Векторная величина в физике: определение, обозначение, примеры

Скаляры и вектора

Скалярные величины в физике являются параметрами, которые могут быть измерены и представлены одним числом. Например, температура, масса и объем являются скалярами, поскольку они измеряются числом градусов, килограмм и кубических метров соответственно.

Согласно определению векторной величины как направленного в пространстве отрезка, она может быть представлена в виде набора чисел (компонент вектора), если ее рассматривать в определенной системе координат. Чаще всего в физике и математике возникают задачи, которые для описания вектора требуют знания его двух (задачи на плоскости) или трех (задачи в пространстве) компонентов.

Определение вектора в n-мерном пространстве

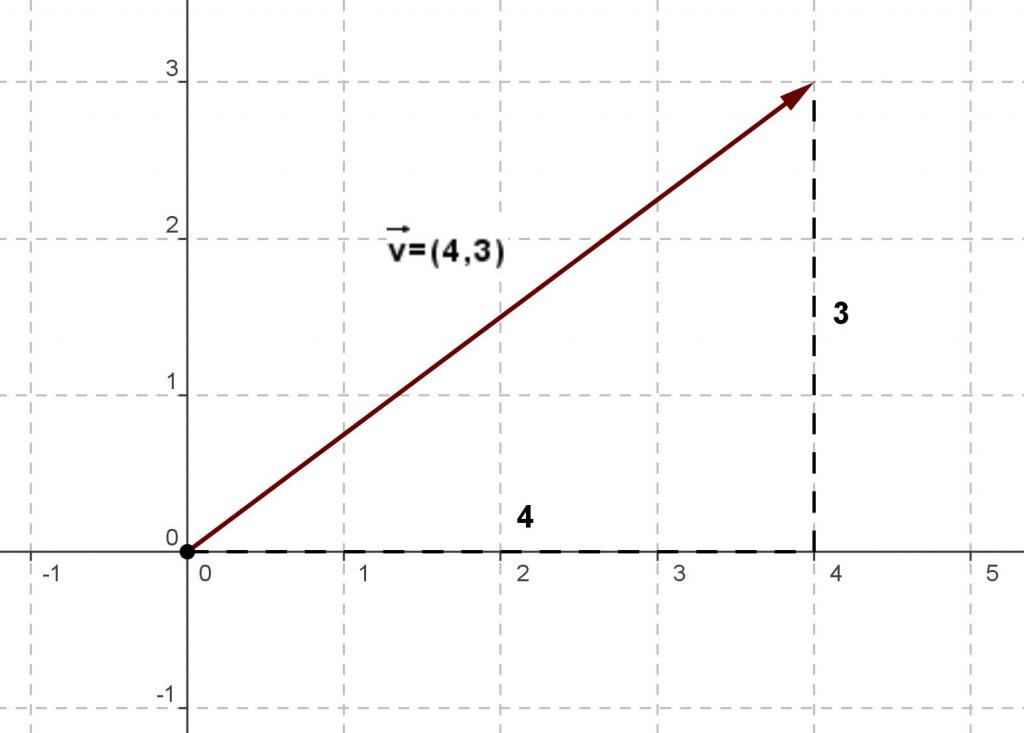
Графическое представление вектора

Графическое представление вектора помогает понять, куда приложена и в каком направлении действует физическая величина. Кроме того, многие математические операции над векторами удобно совершать, используя их изображения.

Математические операции над векторами

Векторные величины, так же как и обычные числа, можно складывать, вычитать и умножать как друг с другом, так и с другими числами.

Под суммой двух векторов понимают третий вектор, который получается, если суммируемые параметры расположить так, чтобы конец первого совпадал с началом второго вектора, а затем, соединить начало первого и конец второго. Для выполнения этого математического действия разработаны три основных метода:

Что касается разницы векторных величин, то ее можно заменить сложением первого параметра с тем, который противоположен по направлению второму.

Умножение вектора на некоторое число A выполняется по простому правилу: на это число следует умножить каждую компоненту вектора. В результате получается также вектор, модуль которого в A раз больше исходного, а направление либо совпадает, либо противоположно исходному, все зависит от знака числа A.

Делить вектор или число на него нельзя, а вот деление вектора на число A аналогично умножению на число 1/A.

Скалярное и векторное произведения

Умножение векторов можно выполнять двумя различными способами: скалярно и векторно.

Скалярным произведением векторных величин называется такой способ их умножения, результатом которого является одно число, то есть скаляр. В матричном виде скалярное произведение записывается как строки компонента 1-го вектора на столбец компонент 2-го. В итоге в n-мерном пространстве получается формула: (A → *B → ) = a₁*b₁+a₂*b₂+. +a_n*b_n.

В 3-мерном пространстве можно определить скалярное произведение иначе. Для этого нужно умножить модули соответствующих векторов на косинус угла между ними, то есть (A → *B → ) = |A → |*|B → |*cos(θ_AB). Из этой формулы следует, что если вектора направлены в одном направлении, то скалярное произведение равно умножению их модулей, а если вектора перпендикулярны друг другу, тогда оно оказывается равным нулю. Отметим, что модуль вектора в прямоугольной системе координат определяется как квадратный корень от суммы квадратов компонент этого вектора.

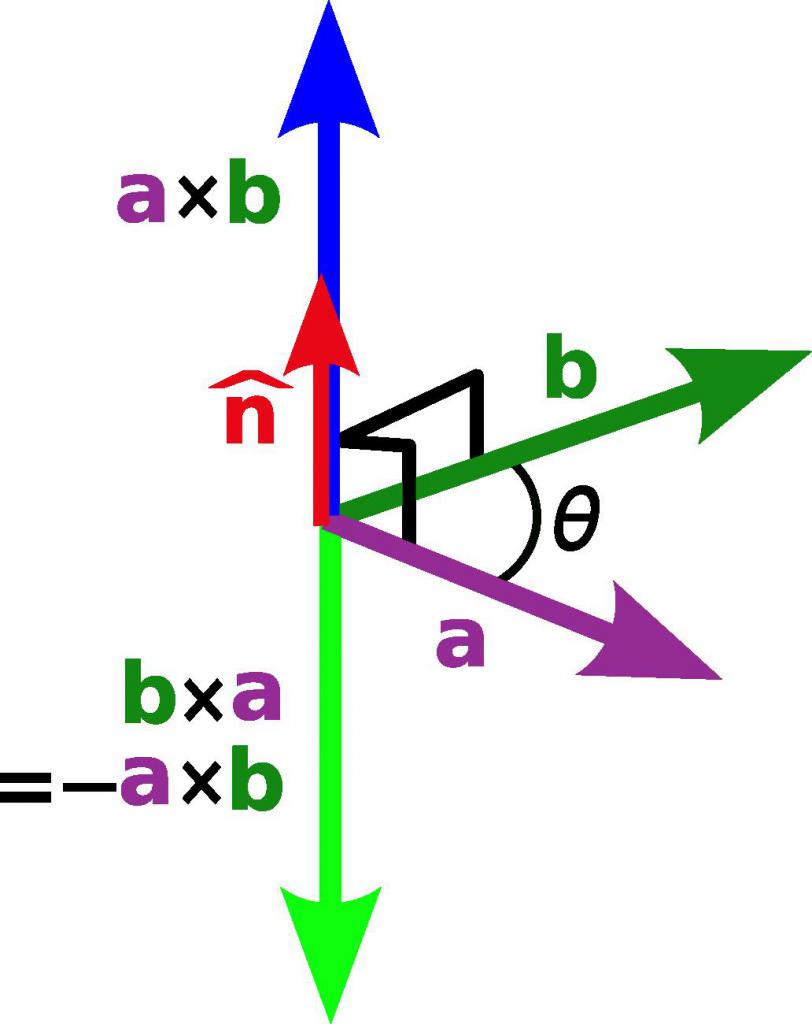
Под векторным произведением понимают такое умножение вектора на вектор, результатом которого также является вектор. Его направление оказывается перпендикулярно каждому из умножаемых параметров, а длина равна произведению модулей векторов на синус угла между ними, то есть A → x B → = |A → |*|B → |*sin(θ_AB), где значок «x» обозначает векторное произведение. В матричном виде этот вид произведения представляется как определитель, строками которого являются элементарные вектора данной системы координат и компоненты каждого вектора.

Как скалярное, так и векторное произведения используют в математике и физике для определения многих величин, например, площади и объема фигур.

Далее в статье приводятся примеры векторных величин в физике.

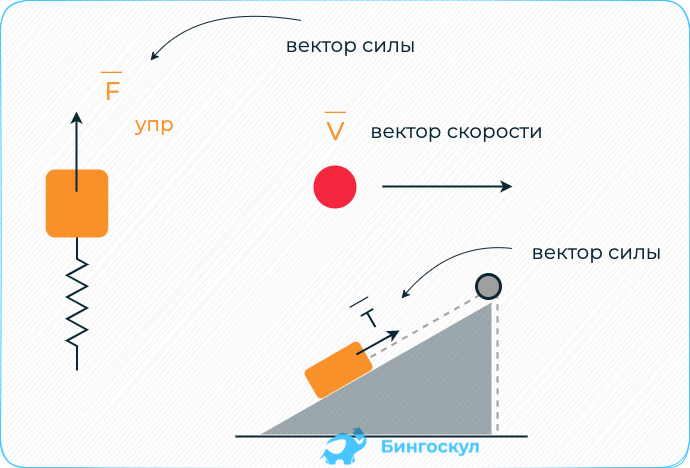
Скорость и ускорение

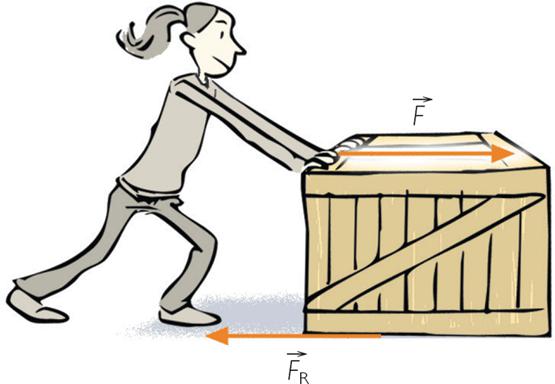
Физическая величина сила

Эта физическая величина широко применяется в физике, поскольку с ней связаны энергетические характеристики процессов взаимодействия. Природа силы может быть самой разной, например, гравитационные силы планет, сила, которая заставляет двигаться автомобиль, упругие силы твердых сред, электрические силы, описывающие поведение электрических зарядов, магнитные, ядерные силы, которые обуславливают стабильность атомных ядер, и так далее.

Векторная величина давление

В физике понятие давления часто используется при изучении явлений в жидкостях и газах (например, закон Паскаля или уравнение состояния идеального газа). Давление тесно связано с температурой тела, поскольку кинетическая энергия атомов и молекул, представлением которой является температура, объясняет природу существования самого давления.

Напряженность электрического поля

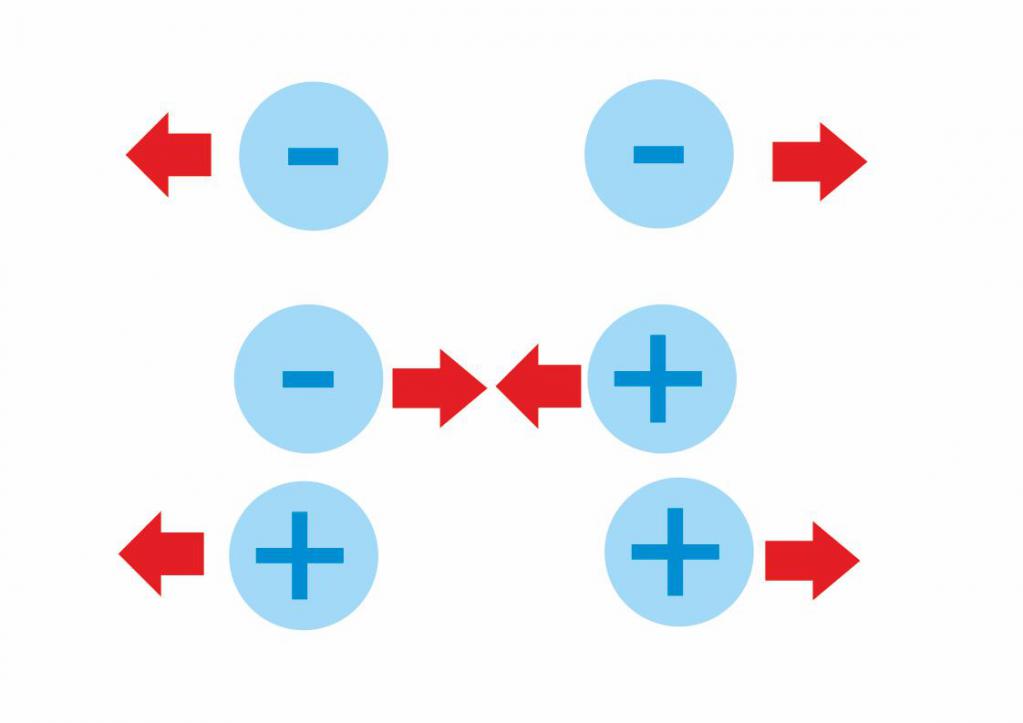
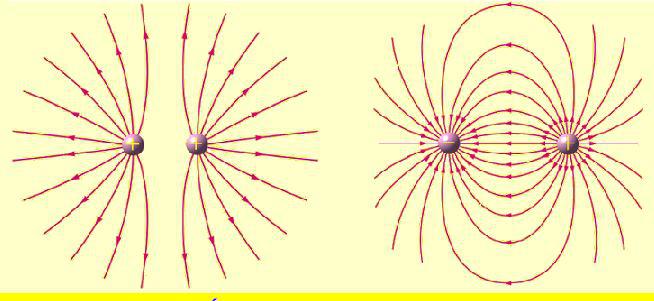
Вокруг любого заряженного тела существует электрическое поле, силовой характеристикой которого является его напряженность. Определяется эта напряженность как сила, действующая в данной точке электрического поля на единичный заряд, помещенный в эту точку. Обозначается напряженность электрического поля буквой E → и измеряется в ньютонах на кулон (Н/Кл). Вектор напряженности направлен вдоль силовой линии электрического поля в ее направлении, если заряд положительный, и против нее, если заряд отрицательный.

Напряженность электрического поля, создаваемого точечным зарядом, можно определить в любой точке, используя закон Кулона.

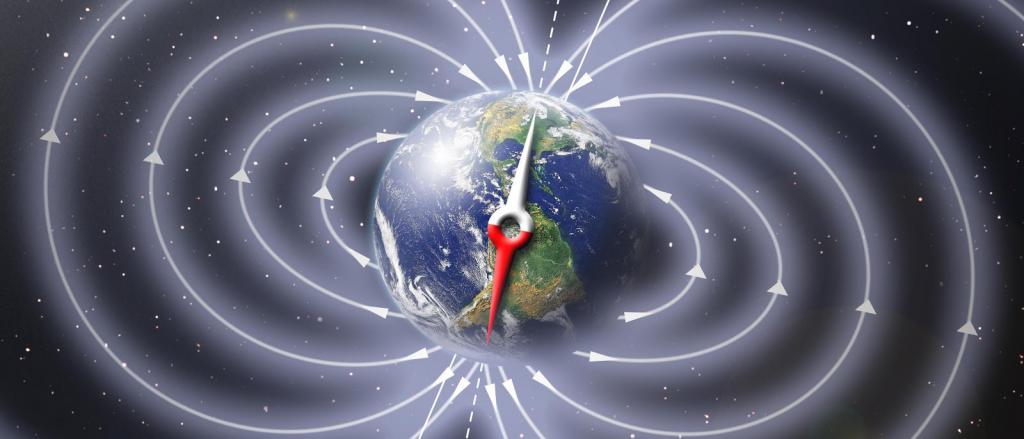
Магнитная индукция

Магнитное поле, как показали в XIX веке ученые Максвелл и Фарадей, тесно связано с электрическим полем. Так, изменяющееся электрическое поле порождает магнитное, и наоборот. Поэтому оба вида полей описываются в рамках электромагнитных физических явлений.

Физическая величина кандела

Еще одним примером векторной величины является кандела, которая вводится в физику через световой поток, измеряемый в люменах, проходящий через поверхность, ограниченную углом в 1 стерадиан. Кандела отражает яркость света, поскольку показывает плотность светового потока.

Источник

Векторы в физике

Закрепленный вектор — упорядоченная пара точек (направленный отрезок, имеющий начало и конец).

Длина вектора — расстояние между началом и концом вектора.

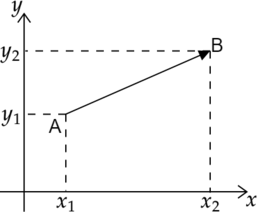
Если задана прямоугольная система координат, и координаты начала и конца вектора заданы в ней парами \(A=(x_1,y_1)\) и \(B=(x_2,y_2)\) соответственно, тогда координаты вектора можно задать \[\overrightarrow=\<\,x_2-x_1, y_2-y_1\,\>\]

Тогда длина вектора \(\overrightarrow\) задается формулой

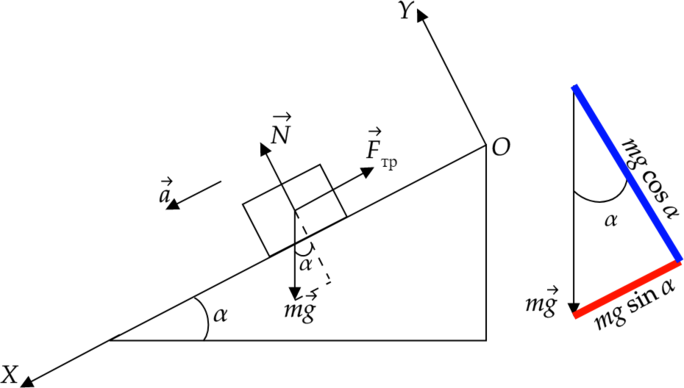
Рассмотрим ситуацию, когда брусок движется по наклонной плоскости:

Исходя из рисунка мы можем записать II закон Ньютона в векторной форме: \[\vec_\text<тр>+m\vec+\vec=m\vec\]

Запишем теперь проекции на оси:

Посмотрим, как получили два вышеприведенных равенства. Направим оси, как на рисунке, тогда по оси \(OY\) ускорение и сила трения на тело не действуют, так как они направлены перпендикулярно этой оси, а проекции сил, перпендикулярных оси, равны нулю.

Сложение векторов можно производить по правилу треугольника или по правилу параллелограмма, рассмотрим на примере.

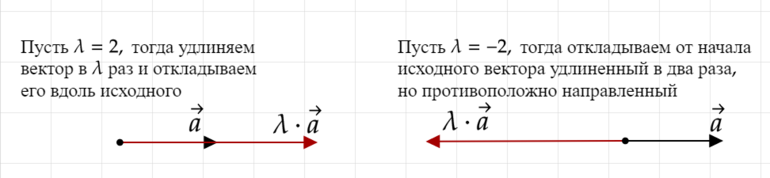
Рассмотрим различные варианты произведения вектора \(\vec\) на какое-то вещественное число \(\lambda\) :

При умножении на нулевое число получается нулевой вектор (вектор нулевой длины);

При умножении на положительное число получается вектор, сонапаравленный исходному вектору (происходит просто “удлинение” или “укорачивание” нашего вектора, направление не меняется);

При умножении на отрицательное число получается вектор, противоположно направленный исходному вектору (происходит “разворот” вектора на 180 градусов и изменение его длины одновременно).

Скалярным произведением векторов называют число, равное произведению длин этих векторов на косинус угла между ними.

Физический смысл скалярного произведения

Источник