Что обозначает величина а в выражении периода колебаний физического маятника

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Физический маятник

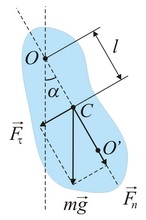
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции. В положении равновесия центр инерции маятника С находится под точкой подвеса маятника O, на одной с ней вертикали (рис. 50). При отклонении маятника от положения равновесия на угол α возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние между точкой подвеса и центром инерции маятника. Знак «–» означает, что вращательный момент стремится вернуть маятник в положение равновесия, т. е. направлен в сторону, противоположную изменения угла Δα. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой J, можно написать:

. (136)

(137)

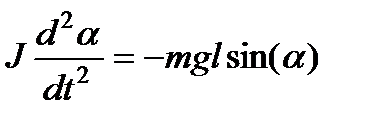
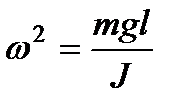
Тогда для малых отклонений, когда выполняется условие sin(α) ≈ α, получаем уравнение гармонических колебаний:

. (138)

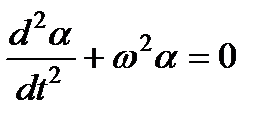
При малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, циклическая частота которых определяется формулой (137). Соответственно, период колебаний физического маятника равен:

. (139)

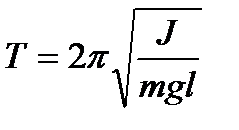
Из сопоставления формул (139) и (134) следует, что математический маятник с длиной

(140)

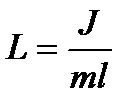
будет иметь такой период колебаний, как и данный физический маятник. Величину (140) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку О’ на рис. 50).

По теореме Штейнера момент инерции маятника l может быть представлен в виде

где J₀ – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника. Подставив (141) в формулу (140), получаем:

. (142)

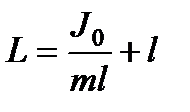
Из (142) следует, что приведенная длина всегда больше l, так что точка подвеса и центр качания лежат по разные стороны от центра инерции.

Подвесим маятник в точке, совпадающей с центром качания О’. В соответствии с (142) приведенная длина в этом случае будет равна

(143)

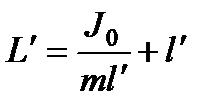
где l’ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l’ = L – l, выражение (143) можно записать следующим образом:

.

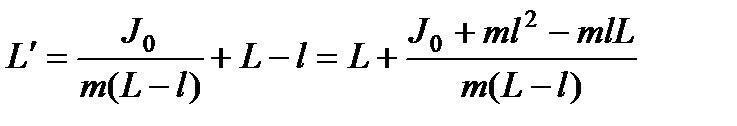
Поскольку J₀ + ml 2 равно моменту инерции относительно первоначальной оси вращения J, и этой же величине, согласно (140) равно выражение mlL, то числитель дроби будет равен нулю. Поэтому L’ = L. Это означает, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Это положение называется теоремой Гюйгенса:

Источник

Период колебаний

Что такое колебательный процесс

Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.

Систему, совершающую колебания, называют колебательной системой или осциллятором.

Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.

Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.

При механических колебаниях, которые относят к категории вынужденных:

Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.

Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.

Определение периода колебаний, формула

Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:

\(x(t)=A\times \cos \left(\omega _<0>t+\phi _ <0>\right)\)

Где \(x(t)\) является отклонением колеблющейся физической величины от равновесного значения;

А представляет собой амплитуду гармонических колебаний;

\(\omega _<0>\) равно циклической или круговой частоте колебаний;

\(\phi _<0>\) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;

\(cp(t)=(co_<0>t+cp_<0>)\) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.

\(\cos \left(\alpha +2\pi \right)=\cos \alpha,\)

Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.

В этом случае фаза будет увеличена на \(2\pi:\)

\(\omega _<0>(t+T)+\phi _<0>=\left(\omega _<0>t+\phi _ <0>\right)+2\pi\)

Из данного равенства можно вычислить период колебаний:

Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:

На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.

Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.

Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:

Смещение \(x=A\times \cos \left(\omega _<0>t+\phi _ <0>\right)\)

Скорость \(v_=\dot=-A\omega _<0>\times \sin \left(\omega _ <0>t+\phi_ <0>\right)=A\omega _<0>\times \cos \left(\omega _ <0>t+\phi_ <0>+\frac<\pi ><2>\right)\)

\(a_=\dot>=\ddot=-A\omega _<0>\times \cos \left(\omega _ <0>t+\phi_ <0>\right)=A\omega _<0>^<2>\times \cos \left(\omega _ <0>t+\phi_ <0>+\pi \right)\)

Как найти период для физического маятника

В случае, когда углы отклонения \(\varphi\) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:

\(F=mg\times \sin \varphi\)

Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла \(\alpha\)

Учитывая малый угол \(\varphi\) уравнение можно записать в следующем виде:

С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:

При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:

В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:

Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:

В таком случае для расчета периода колебаний математического маятника будет использоваться формула:

Исходя из расчетов, можно сделать следующие выводы:

В приведенных формулах:

Примеры решений

Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.

Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.

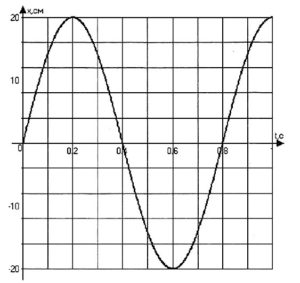
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.

\(x(t)=A\sin 2\pi Vt=0.2\sin 2\pi \times 1.25t=0.2\sin 2.5\pi t\)

Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: \(x(t)=0.2\sin 2.5\pi t\)

Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.

Период колебаний математического маятника рассчитывается по формуле:

Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:

Ответ: длина математического маятника примерно составляет 0,16 метра.

Источник

Формула периода колебаний математического маятника

Математический маятник

Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.

Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.

Формула для периода колебаний математического маятника

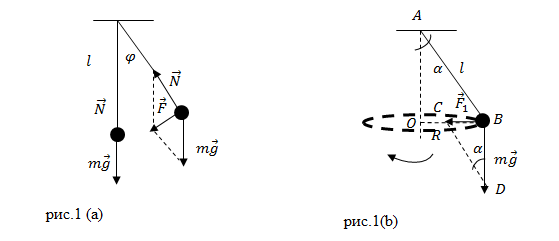
Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($\overline$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис.1 (b)). Груз в этом случае перемещается по окружности. Период интересующих нас колебаний будет совпадать с периодом конического движения груза. Период обращения конического маятника по окружности равен времени, которое тратит груз на один виток по окружности:

Рассмотрим подобные треугольники: AOB и DBC (рис.1 (b)).

Приравниваем правые части выражений (2) и (3), выражаем скорость движения груза:

Полученную скорость подставим в формулу (1), имеем:

Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.

Примеры задач с решением

Решение. За основу решения задачи примем формулу периода математического маятника:

Выразим из (1.1) ускорение свободного падения:

Вычислим искомое ускорение:

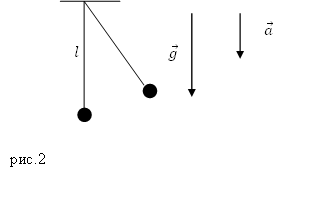
Решение. Сделаем рисунок.

1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:

Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:

Источник