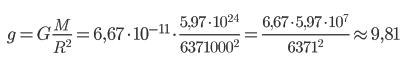Что обозначает vox в физике
Каталог файлов
КИНЕМАТИКА (ФОРМУЛЫ)
Закон сложения скоростей (для поступательного движения системы отсчета)
v1 = v12 + v2,
где v1 − скорость первого тела (например, относительно земли), v12 − скорость первого тела относительно второго тела (подвижной системы отсчета), v2 − скорость второго тела (относительно земли). Аналогичный вид имеют закон сложения перемещений
S1 = S12 + S2
и закон сложения ускорений
a1 = a12 + a2.
Эту формулу в виде
v12 = v1 − v2
называют формулой для относительной скорости двух тел.
Средняя скорость при неравномерном движении по прямой
Скорость и перемещение при равноускоренном движении по прямой
Свободное падение (vo = 0). Скорость и перемещение (ось y направлена вниз, ay = g)
Бросок вертикально вверх с начальной скоростью vo. Скорость и перемещение (ось y направлена вверх, voy = vo, ay = −g):
Бросок под углом к горизонту с начальной скоростью vo. Проекция скорости и перемещения (ось x направлена горизонтально, ось y − вертикально вверх):
Объем и масса (жидкости, газа), проходящие через сечение S струи за время Δt (уравнение расхода):
ΔV = SvΔt,
Δm = ρΔV = ρSvΔt,
где v − скорость струи, ρ − плотность (жидкости, газа).
Ускорение свободного падения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей. 🤓
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
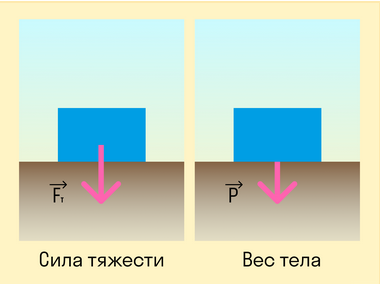
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Формула ускорения свободного падения
g — ускорение свободного падения [м/с 2 ]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
Для этого нам понадобятся следующие величины:
Подставим значения в формулу:
И кому же верить?
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Небесное тело
Ускорение свободного падения, м/с 2
Диаметр, км
Расстояние до Солнца, миллионы км
Масса, кг
Соотношение с массой Земли
Список обозначений в физике
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Содержание
Шрифты
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Латинская азбука
В силу исторических причин, многие из обозначений используют латинские буквы — от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком). Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква 
Обозначение с несколькими буквами
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Латинские названия математических функций и операций, которые часто используются в физике:
| Символ | Значение |
|---|---|
| div | дивергенция |
| grad | градиент |
| lim | предел |
| rect | прямоугольная функция |
| rot | ротор |
| sgn, sign | Signum-функция |
| sinc | функция sinc |
Греческая азбука
Крупные греческие буквы, которые в написании похожи на латинские (
Кириллица
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Специальные символы
| Символ | Значение |
|---|---|
 | оператор Гамильтона |
 | дивергенция |
 | ротор |
 | даламбертиан |
 | векторное произведение |
 | тензорное произведение |
 | частная производная |
 | возведена постоянная Планка |
| ! | факториал |
 | слэш-обозначения Фейнмана |
 | внешнее произведение |
 | интеграл от a до b |
 | интеграл по контуру |
| Ø | диаметр |
Скобки
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Например, f(x, y) означает, что величина f является функцией x и y.
| Символ | Значение |
|---|---|
 | векторное произведение, коммутатор между двумя операторами, скобка Паерлза |
 | скалярное произведение |
 , ,  | бра и кет нотация, средняя величина |
 | скобки Пуассона |
 | модуль |
 | норма |
Диакрические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакрические знаки добавлены для примера к букве x.
| Символ | Значение |
|---|---|
 | первая производная по времени |
 | вторая производная по времени |
 | первая производная |
 | вторая производная |
 | векторная величина |
 | средняя величина, античастица, комплексно сопряженное |
 | оператор |
 | подчёркивает отличие величины от предварительно принятой |
 | оператор рождения |
 | оператор эрмитовых спряжений |
| Å | ангстрем |
Нижние и верхние индексы
Обозначения физических величин часто имеют нижний, верхний, или оба индекса. Обычно нижний индекс обозначает характерный признак величины, например ее порядковый номер, тип, проекцию и т. п.. Верхний индекс обозначает степень кроме случаев когда величина является тензором.
Графические обозначения
Для наглядного обозначения физических процессов и математических операций используются графические обозначения: Фейнмановские диаграммы, спиновые сети и графические обозначения Пенроуза.
См. также
Примечания
Источники
Ссылки
Полезное
Смотреть что такое «Список обозначений в физике» в других словарях:
Таблица математических символов — В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия
Математические обозначения — Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
Знаковые системы — Список знаковых систем (систем обозначений и т.п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия
Дирак, Поль Адриен Морис — Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия
Дирак — Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902( … Википедия
Лейбниц, Готфрид Вильгельм — Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия
Мезон — У этого термина существуют и другие значения, см. Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия
Альтернативные теории гравитации — Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия
МОНД — Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации часто… … Википедия
Новое в блогах
Физическая интерпретация i
В качестве гипотезы интерпретации i в реальности можно предложить следующую идею. Величина мнимой части комплексного числа является вполне реальной величиной, но расположенной за границей рассматриваемого явления, например, за пределами частицы. Умножение комплексного числа на i приводит к переходу самого акта рассмотрения через условную границу частицы, в результате чего мнимая часть становится действительной, а действительная становится мнимой, расположенной за границей рассматриваемой области только теперь уже с другой ее стороны.
Физические уравнения, содержащие мнимую часть, описывают явления внутри частицы, однако внешние явления также оказывают влияние на внутренние явления в частице, но это влияние не полное, поскольку отделено границей.

Думаю, что Вы и не собирались.
Что требуется от Вас?
— найти физический смысл «мнимых» величин.
О чем пишете Вы:
— для чего используются мнимые числа
— о мнимой операции
То есть о чем-то о смежном, но ответа на поставленный вопрос нет.
Сосредоточьтесь на физическом смысле переменных, находящихся в мнимой части комплексного числа.
Кстати, это очень важно для выявления критерия различения внутренних и внешних явлений и для различения внешних действий (дальнодействия и близкодейстия) и внутренних действий.


Есть большая разница между реальностью и символами ее описывающими. Если вы даже найдете на хлебе буквы х, л и т.д, то смысла в этом не будет.
Олег, помогите новичку разобраться с мнимой частью, «в реальности».
ссылка на maxpark.com
Подскажите ему каким образом произведение двух мнимых частей может стать действительным числом.
А также прокомментируйте ссылка на forum.if4.ru

Но желание «помогать» не возникло. Вы говорите о совершенно разных вещах. Если в ваш разговор влезу еще и я, то это будет всего лишь третья тема, которая будет противоречить (или находиться в другом измерении) по отношению к вашему обсуждению.
Вам же я могу сказать, что, измеряя параметры некоторой электрической схемы на некоторой частоте, мы измеряем полное сопротивление цепи и угол между напряжением и током, что дает нам вектор импеданса. На другой частоте вектор получится иным, но на любой из частот мы можем разложить вектор в плоскости с координатами Re/Im на два ортогональных вектора.
Интересным является поведение конца этого вектора на вышеуказанной плоскости. Если для всех частот отметить точками координаты этого вектора для RC цепи, то они сольются в правильную полуокружность. То же и для RL цепи, только в другом квадранте.
Говорить же о физическом смысле Re и Im не имеет смысла, так как физический смысл не должен зависеть от частоты.

Я с удовольствием ответил бы на ваши вопросы, но, как я понимаю, они не ко мне. В этом случае лучше обратиться прямо к ним, иначе вашего вопроса они могут не заметить.

К примеру, известная формула Эйнштейна про зависимость массы от скорости. Если скорость объекта выше скорости света, то масса объекта становится комплексной. Т.е. часть массы объекта «уходит» в скрытое измерение. Что и позволяет объекту перемещаться выше скорости света

Взаимопереходы мнимых частей и действительных – совершенно неудивительны, если допустить, что это лишь проекции частицы, имеющей мерность не только в обычном 3х-мерном пространстве, но и в свёрнутых, непроявленных измерениях. Не вижу в этом ничего невозможного и невероятного.
Поэтому неудивительно, что проекция энергетического взаимодействия на реальное пространство оказывается зависимой от параметров объекта в скрытом пространстве (и наоборот). Это есть проявление взаимозависимости частей объекта друг от друга.


Так какими они (мнимые части параметров) являются в реальности?
Чем в реальности отличаются Еr и Em?
Разумеется, между проявленными и непроявленными измерениями есть разница. На макро-уровне мы можем видеть, чувствовать и измерять только Re-проекцию комплексного пространства и комплексных частиц. Скрытые измерения проявляются только на уровне микро-мира, соответствующего размеру суперструн

А то мало ли ещё какие общепринятые концепции, Вы исключите из реальности и причислите к «инструментам мышления».
Математика и физика не отказывает пространству в реальности. И я не вижу причин делать это.