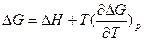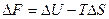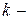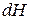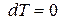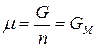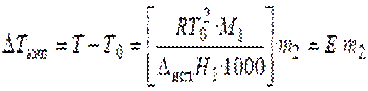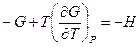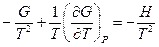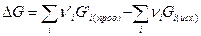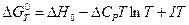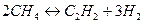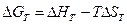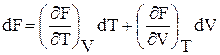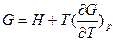Что обозначают буквы в уравнении гиббса гельмгольца u f ts
Энергия Гиббса. Энергия Гельмгольца. Направление процесса.
Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).
Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.
Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.
При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.
Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:
При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:
Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).
Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:
Энтальпийный и энтропийный факторы и направление процесса
Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:
Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.
Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.
А при при ΔS 0 Величина ΔG 0 р-ции позволяет определить, будет ли данная реакция, находящаяся в стандартных условиях, протекать самопроизвольно в прямом или обратном направлении. Аналогично теплоте образования, энергии Гиббса образования простых веществ равны нулю. Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением: Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением: ΔA — величина, которая не зависит от пути, а зависит только от исходного и конечного состояния системы, т.е. ΔA также, как и другие рассмотренные термодинамические величины, является функцией состояния. Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых А уменьшается. Таким образом, при ΔA 0 – в обратном направлении, а при ΔA=0 система находится в состоянии равновесия. Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия: Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура. Если K>>1, т.е. реакция идет в прямом направлении, то ΔG 0 ˂˂0. Если K 0 >>0 Если K=1, то ΔG 0 =0 В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG 0 можно связать с ЭДС гальванического элемента следующим соотношением: nF – количество прошедшего электричества E 0 – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии. При самопроизвольном протекании процесса, его ΔG 0. Порог реакционной способности веществ для большинства реакций имеет значение ΔG 0 ≈41 кДж/моль. То есть, если ΔG 0 0 >+41 кДж/моль, то процесс неосуществим в любых реальных и стандартных условиях. Уравнение Гиббса-Гельмгольца позволяет определять изменение энергии Гиббса, сопровождающее химические реакции при любой заданной температуре, если известна зависимость теплоты химических реакций от температуры. Для вывода уравнения запишем ещё раз формулу, определяющую энергию Гиббса (III, 17): Из уравнения (III, 22) и теоремы 1 следует, что Полученное уравнение перепишем в следующем виде: Разделим обе части полученного уравнения на Т 2 : Нетрудно показать, что Для химической реакции это соотношение можно записать через изменение энергии Гиббса и энтальпии: где Выражение(III, 34)и являетсяизвестным уравнением Гиббса-Гельмгольца. Оно лежит в основе аналитического вычисления зависимости Перед рассмотрением использования этого уравнения условимся применять его преимущественно к стандартным условиям, что может быть учтено, если Возьмем неопределенный интеграл соотношения (III, 35): где I – константа интегрирования, которая вычисляется для каждой конкретной реакции. Чтобы вычислить интеграл в правой части полученного уравнения, подставим выражение для Рассмотрим зависимость 1. Теплоемкости исходных веществ и продуктов различны, но их разность постоянна, т.е. Анализ данных, полученных для различных процессов, показывает, что основная термодинамическая характеристика химической реакции Например, стандартная энергия Гиббса реакции с повышением температуры изменяет знак с положительного на отрицательный при Вернемся еще раз к определению энергии Гиббса (смотри (III, 17)): Применив это выражение к изотермическому процессу при постоянном давлении, можем записать: Эта формула полезна тем, что она указывает на изменение энтропийного члена To определите состояние, 1 внешний параметр V (объем) вместо механического параметра AV a2,…Если вам нужен набор формул (4.3) и (4.5) из более общей формулы(см. Главу 3,§ 3, стр.) ТДС = дю + ^alderuto (4.3 ’) ДФ = — СДТ-2 л, дар(4.5 ’) Итак, обобщенная сила Ai%сопряженная для параметра определяется следующим соотношением: (ду (ДФ\, в 7、. А давление P = Aj задается реляционным выражением (4.7). Обычно объем V-ax является единственным внешним параметром. Людмила Фирмаль Заметим, что эти уравнения справедливы для приращений//и G изотермического процесса при постоянном давлении. ДА =GG-T ^ ^ — (4.11) То же самое верно и для приращений U и F в постоянном объеме.Оба уравнения могут быть объединены в 1.At постоянное давление и температура、 ^ max—AG (максимальная работа), Qp = hH (поглощает тепло). (4-12) Аналогично, при постоянном объеме и температуре = ГВ = У.(4.13) Так что можно писать в самом общем виде _ т и Т1 Д ^ Макс. — Макс i 1 fij» Или (4.14) Д ^ Макс _ г dt. Где Q-количество тепла, поглощенного в процессе f MJ + P&V(P = const), Q = <да const). — Спросил я. Химические реакции, которые происходят в элементах Weston, можно описать следующим образом: Cd 4-2Hg + — >Cd2 + — f 2Hg(Cd + Hg2S04 — > CdS04 + 2Hg). Электродвижущая сила этого элемента задается эмпирической формулой Ф (Болт)= 1.0183-4.06•10 «5(Г-293°К). а. какова максимальная работа, которая может быть достигнута в результате превращения 1 моля Cd в реакции, протекающей с элементом 20°C? a. рассчитайте количество поглощенного тепла. Решение also.In в реакциях, которые происходят с элементом, заряд в 2 единицы перемещается от ртути к кадмию. Реакция экзотермическая. Людмила Фирмаль Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института В изолированных системах энтропия только увеличивается и при равновесии достигает максимума. Поэтому она может быть использована в качестве критерия возможности протекания самопроизвольных процессов в таких системах. Однако на практике большинство процессов происходит в неизолированых системах, вследствие чего для них надо выбрать свои критерии направления самопроизвольных процессов и достижения равновесия. Такие критерии выражаются иными термодинамическими функциями, отличными от энтропии. Они называются характеристическими функциями. Рассмотрим объединенный первый и второй закон термодинамики в дифференциальной форме: TdS ³ dU + dA’ + pdV, (36). Выразим отсюда элементарную полезную работу dA’: Рассмотрим два случая: 1) Пусть система переходит обратимо из состояния 1 в состояние 2 при V = const, Т = const, т.е. рассмотрим обратимый изохорно-изотермический процесс. Получим (т.к. dV = 0): Под знаком дифференциала стоит некоторая функция состояния. Обозначим ее через F: и назовем энергией Гельмгольца (старое название: изохорно-изотермический потенциал). Тогда получим: Если проинтегрировать (40), то получим: величина DF = F2 – F1 – изменение энергии Гельмгольца, а –DF = F1 – F2 – убыль энергии Гельмгольца. Энергия Гельмгольца является одним из так называемых термодинамических потенциалов. 2) Рассмотрим обратимый изобарно-изотермический процесс (р = cosnt, Т = cosnt) и проанализируем соотношение (38): dА’ = – dU +TdS – pdV = – dU +d(TS) – d(рV) = – d (U – TS + pV) = – d(H – TS). Под знаком дифференциала стоит другая функция состояния. Обозначим ее через G: и назовем энергией Гиббса (старое название: изобарно-изотермический потенциал). Тогда получим: dА’ = – dGр, Т (43) Проинтегрировав (43) получаем: Здесь DG = G2 – G1 – изменение энергии Гиббса, – DG=G1 – G2 – убыль энергии Гиббса. В ходе обратимого перехода системы из состояния 1 в состояние 2 при постоянных давлении и температуре совершаемая системой полезная работа равна убыли энергии Гиббса (– DG). Для необратимых процессов, т.к. А’необр Изменения термодинамических потенциалов можно рассматривать как критерии возможности протекания самопроизвольных процессов и равновесия в термодинамических системах. В ходе самопроизвольного процесса, протекающего в соответствующих условиях, система сама совершает работу (А’>0) тогда при V,T=const, для необратимого самопроизвольного процесса точка В – соответствует равновесному состоянию (здесь DПх,у = 0). 2.5 Характеристические функции. Уравнения Гиббса–Гельмгольца. Характеристическими функциями называются такие функции состояния системы, посредством которых и их частных производных могут быть выражены в явной форме все термодинамические свойства системы. Из дифференциальной формы объединенного первого и второго законов термодинамики для обратимых процессов выразим величину dU: TdS = dU + dA’ + pdV, откуда dU = TdS – dA’ – pdV. (45) Если полезная работа отсутствует (т.е. dA’ = 0), то получим: Вспомним теперь следующие соотношения: G º H – TS = U + pV – TS (47) Если найти значения полных дифференциалов dG, dF из соотношений (43)-(44) и учесть соотношение (46) для dU, то можно получить следующие выражения для dG, dF: На основании соотношений (49)–(50) можно прийти к выводам, что тогда, записав значения соответствующих полных дифференциалов для dG, dF через соответствующие частные производные, например, и сравнив их с выражениями (49)–(50), можно получить следующие выражения для определения термодинамических свойств: Таким образом, мы показали, что G, F являются характеристическими функциями. C помощью полученных выше соотношений можно получить выражения, называемые уравнением (или уравнениями) Гиббса-Гельмгольца. Из уравнений (47) и (48) легко получить следующие выражения, учитывая, что температура – постоянная: Так как, Последние два равенства и есть искомые зависимости Зависимость энергии Гиббса от температуры и давленияΔH – TΔS = U + pV– TΔS = G(7.21) Гиббса можно получить уравнения Гиббса-Гельмгольца: характеризующие запас свободной энергии для данного состояния системы в изотермических условиях. На основе этих уравнений получают уравнения Гиббса-Гельмгольца для изменения термодинамических потенциалов: Эти уравнения наиболее применимы для расчета изменений функций Гельмгольца и Гиббса при протекании химических реакций. Они связывают максимально полезную работу, при переходе системы из состояния 1 в состояние 2 с тепловым эффектом перехода системы из состояния 1 в состояние 2. Легко показать, что т.е. энергия Гиббса отличается от изменения энергии Гельмгольца на величину т.е. на изменение числа молей газообразных продуктов в ходе реакции. 2…Хингидронный электрод 71.Хингидронный электрод 3…Теория гетерогенного катализа активного комплекса Кобозева. Теория гетерогенного катализа активного комплекса Кобозева. Теория активных ансамблей (Кобозев) Предполагает, что активными центрами служат атомы, беспорядочно расположенные на поверхности твердого тела (аморфная, докристаллическая фаза). Применима, когда на поверхности носителя малое количество kt-металла (Рt на силикагеле). Поверхность твердого тела имеет блочное строение с геометрическими и энергетическими барьерами. Атомы kt под действием теплового движения могут мигрировать из одного блока в другой. Несколько атомов Me внутри области миграции называются ансамблем, содержащим разное число атомов. Каталитическим действием обладают ансамбли с определенным числом атомов металла na – активные ансамбли. Большинство блоков содержат среднее число атомов. Число n-атомных ансамблей рассчитывается по формуле Пример: 1) (kt-Рt на силикагеле) Для этих реакций na=1, это объясняется тем, что лимитирующей стадией является образование промежуточного соединения перекисного характера из атома металла с молекулой O2. Билет 24 1…Химический потенциал Химический потенциал. Выражения I закона термодинамики справедливы при условии неизменности количеств составляющих систему веществ. Количество взаимодействующих веществ и продуктов реакции определяется числом моль Для С учетом (87) получим: Химический потенциал можно выразить через частные производные и других термодинамических потенциалов и аналогично уравнению (86) выразить энергию Гельмгольца Химический потенциал размерная величина – Химический потенциал имеет физический смысл парциальной мольной работы при изменении числа моль данного компонента на единицу при постоянных внешних параметрах и числах моль всех других компонентов, составляющих раствор. Для изобарно-изотермических условий, когда Для однокомпонентной системы из (87), получим: где Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, химический потенциал индивидуального компонента тождественен мольной энергии Гиббса. 2…Криоскопия и эбулиоскопия Криоскопия. Криоскопия– метод определения молекулярных масс по понижению температуры замерзания раствора. При охлаждении растворов наблюдается их замерзание. Температура замерзания – температура, при которой образуются первые кристаллы твердой фазы. Если эти кристаллы состоят только из молекул растворителя, то температура замерзания раствора (Т) всегда ниже температуры замерзания чистого растворителя (Тпл). Разность температур замерзания растворителя и раствора называют понижением температуры замерзания раствора. Количественная зависимость понижения температуры замерзания от концентрации раствора выражается следующим уравнением: где М1 — молярная масса растворителя, DплН1 — энтальпия плавления растворителя, m2 — моляльность раствора; K – криоскопическая постоянная, зависящая от свойств только растворителя, равная понижению температуры замерзания раствора с моляльностью растворенного в нем вещества, равной единице. На рис. 3 представлена температурная зависимость давления насыщенного пара над чистым жидким и твердым растворителем (кривые ОА и ОD) и его парциального давления в паре над растворами разных составов (кривые ВО¢ и СО¢¢) для случая, когда растворенное вещество нелетуче. Кривые ОА¢, O¢B¢,O¢¢C показывают ход с температурой давления паров над переохлажденным и чистым растворителем (ОА¢) и растворами соответствующих составов (О¢B¢, O¢¢C). Рис. 3. Зависимость давления насыщенного пара растворителя от температуры. Кристаллы растворителя будут находиться в равновесии с раствором, если давления пара растворителя над твердой и жидкой фазами будут равны, т.е. когда кривая ОD пересечет кривые ВВ¢, CC¢ при соответствующих температурах Tкр¢ и Tкр¢¢. Температуры, отвечающие этому условию, будут ниже температуры замерзания чистого растворителя (Tкр – тройная точка растворителя). Понижение точки замерзания и повышение точки кипения растворов, их осмотическое давление не зависят от природы растворенных веществ. Такие свойства называют коллигативными. Эти свойства зависят от природы растворителя и концентрации растворенного вещества. Как правило, коллигативные свойства проявляются, когда в равновесии находятся две фазы, одна из которых содержит растворитель и растворенное вещество, а вторая – только растворитель. Эбулиоскопия. Эбулиоскопия— метод определения молекулярных масс по повышению точки кипения раствора. Температурой кипения раствора называют температуру, при которой давление пара над ним становится равным внешнему давлению. Если растворенное вещество нелетуче, то пар над раствором состоит из молекул растворителя. Такой раствор начинает кипеть при более высокой температуре (Т) по сравнению с температурой кипения чистого растворителя (Т0). Разность между температурами кипения раствора и чистого растворителя при данном постоянном давлении называется повышением температуры кипения раствора. Эта величина зависит от природы растворителя и концентрации растворенного вещества. Жидкость кипит, когда давление насыщенного пара над ней равно внешнему давлению. При кипении жидкий раствор и пар находятся в равновесии. Можно показать, что в случае, если растворенное вещество нелетуче, повышение температуры кипения раствора подчиняется уравнению где М1 — молярная масса растворителя, DиспН1 — энтальпия испарения растворителя, m2 — моляльность раствора (количество моль растворенного вещества в расчете на 1 кг растворителя); Е – эбулиоскопическая постоянная, равная повышению температуры кипения одномоляльного раствора по сравнению с температурой кипения чистого растворителя. Величина Е определяется свойствами только растворителя, но не растворенного вещества. 3…Гетерогенные химические реакции. Влияние температуры на протекание гетерогенной химической реакции. 89. Гетерогенные химические реакции. Влияние температуры на протекание гетерогенной химической реакции. Увеличение скорости химической реакции с ростом температуры, на первый взгляд, можно объяснить возрастанием скорости теплового движения молекул исходных веществ. Это должно приводить к увеличению числа соударений между ними, несмотря на то, что общее количество молекул осталось неизменным. Однако, как показали расчёты, число соударений между частицами, находящимися в газовых и жидких средах за единицу времени, всегда достаточно велико. Так, в 1 см 3 газа (при н.у.) за одну секунду происходит 1 · 10 28 столкновений между молекулами. Если бы каждое из них приводило к образованию конечных продуктов, то подавляющее большинство химических реакций протекали бы практически мгновенно, т.е. со взрывом. На практике этого не наблюдается, т.к. не все соударения между молекулами исходных веществ являются «успешными». Установлено, что для многих реакций число таких «успешных» соударений в 10 15 –10 20 раз меньше, чем общее число соударений. Протекание реакции становится возможным только в том случае, если столкнувшиеся молекулы обладают достаточным запасом внутренней энергии. Если её значение равно какой-то определённой величине или больше её, то реакция осуществится (в противном случае – нет). Такие молекулы называются активными, а соударения между ними – эффективными. Обычно доля активных молекул реагентов, по сравнению с их общим числом, для большинства реакций невелика. При повышении температуры увеличивается запас внутренней энергии молекул. Всё большее их число становятся активными. Как следствие этого, возрастает доля эффективных соударений между молекулами за единицу времени, а значит и скорость химической реакции. При повышении температуры концентрации исходных веществ в реакционной смеси практически не изменяются. Значит, увеличение скорости реакции в соответствии с главным кинетическим уравнением должно быть связано с возрастанием её константы скорости. Голландский учёный Вант-Гофф опытным путём определил, что для химических реакций (имеющих нормальный тип зависимости скорости от температуры) при повышении температуры на каждые 10 градусов величина константы скорости возрастает в 2-4 раза. Причём для каждой химической реакции это число является постоянным и может принимать из указанного интервала как целочисленные (2, 3, 4) значения, так и дробные. Оно определяется экспериментально, называется температурным коэффициентом скорости химической реакции или коэффициентом Вант-Гоффа и обозначается греческой буквой γ: Более точную зависимость константы скорости от температуры дает уравнение Аррениуса: Энергия активации – избыток энергии по сравнению со средней энергией реагирующих веществ, который необходим для того, чтобы соударения были результативными 1.Теплоёмкость. Средняя и истинная теплоемкость. Зависимость теплоты реакции от температуры. Дата добавления: 2018-04-04 ; просмотров: 2212 ; Мы поможем в написании вашей работы!Всегда ˂0 Реакция самопроизвольна при любых температурах, обратная реакция всегда несамопроизвольна >0 ˂0 Всегда >0 Реакция несамопроизвольна при любых температурах, обратная реакция самопроизвольна ˂0 ˂0 При низких температурах ˂0, при высоких температурах >0 Реакция самопроизвольна при низких температурах, обратная реакция становится самопроизвольной при высоких температурах >0 >0 При низких температурах >0, при высоких температурах ˂0 Реакция несамопроизвольна при низких температурах, но при высоких температурах становится самопроизвольной Уравнение Гиббса-Гельмгольца
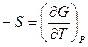

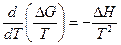
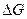
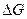
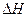
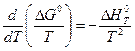

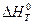
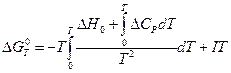


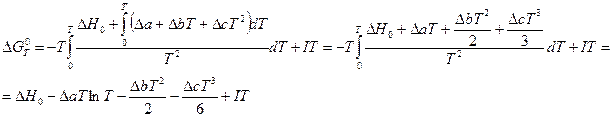
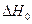
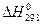
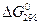
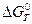
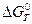
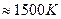

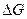
Уравнения гиббса — гельмгольца






Уравнения гиббса — гельмгольца
Термодинамические потенциалы. Энергия Гиббса. Энергия Гельмгольца



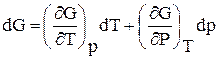
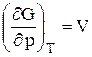
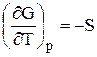
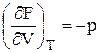

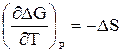
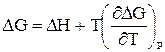
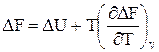
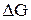
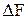
Зависимость энергии Гиббса от давления и температуры, уравнение Гельмгольца-Гиббса