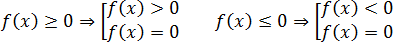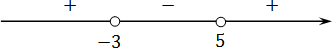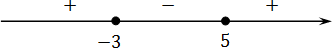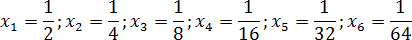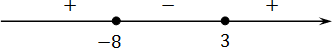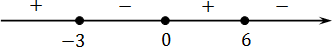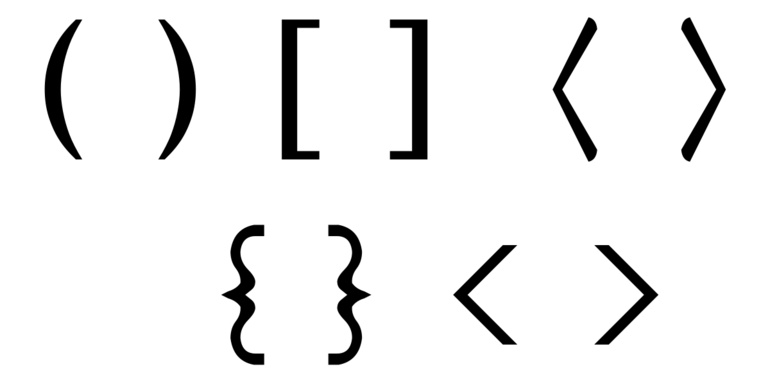Что обозначают круглые и квадратные скобки в неравенствах
Как записать ответ неравенства
Впрочем, мы рекомендуем освоить запись ответа неравенства в математических обозначениях сразу, так как в любом случае в старшей школе и затем в университете будут требовать именно такую запись ответа.
Перед разбором, как записывать ответ неравенства математическими знаками, вспомним расшифровку и обозначение этих знаков.
| Знак | Расшифровка |
|---|---|
| ∈ | «Принадлежит» Легко запомнить знак, как зеркальное отображение русской буквы « Э » или как символ евро « € », но только с одной палочкой посередине. |
| ( … ) | «Круглые скобки» Используются, когда число на границе интервала НЕ входит в сам интервал. На числовой оси такие числа обозначают «пустой» точкой. |
| [ … ] | «Квадратные скобки» Используются, когда число на границе интервала входит в сам интервал. На числовой оси такие числа обозначают «заполненной» точкой. |
| ∪ | «Объединение» Знак похож на подковку. Используется для объединения двух и более интервалов. |
| + ∞ | «Плюс бесконечность» Изображается как цифра « 8 » на боку со знаком « + » слева. Обозначает бесконечность на положительном (правом) краю числовой оси. |
| − ∞ | «Минус бесконечность» Изображается как цифра « 8 » на боку со знаком « − » слева. Обозначает бесконечность на отрицательном (левом) краю числовой оси. |
Перейдем к непосредственной записи ответа неравенства. Рассмотрим и решим линейное неравенство.
Мы решили линейное неравенство, теперь запишем его ответ с помощью математических знаков.
Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.
Итак, мы изобразили ответ неравенства на числовой оси. После этого запишем слово «Ответ:» и за ним запишем « x ∈ ». Такая запись читается как «икс принадлежит».
Взглянув на рисунок ответа на числовой оси, мы видим, что область решений начинается с числа « 14 ». Число « 14 » не входит в область решений («пустая» точка на оси). Значит, используем круглую скобку.
Нам остается понять, где заканчивается область решений справа. Правильный ответ — справа область заканчивается в положительной бесконечности « + ∞ ».
На числовой оси на обоях краях слева и справа соответственно расположены «минус» и «плюс» бесконечности. Как правило, их не рисуют на числовой оси лишний раз, т.к. их наличие на оси подразумевается.
Запишем окончательный ответ.
Знаки « + ∞ » и « − ∞ » всегда записываются с круглыми скобками.
Разберем другой пример.
Также как и в предыдущем примере всегда начинаем записывать
ответ с записи « x ∈… ».
В ответе « x ≤ 8 » область решений начинается с « − ∞ » и заканчивается на « 8 », которое входит в ответ. Значит, « 8 » будет с квадратной скобкой. Так и запишем в ответе.
Запись ответа неравенства для квадратных неравенств
При решении квадратных неравенств часто может получаться несколько интервалов в ответе. Разберемся, как их записывать в ответ. Рассмотрим пример квадратного неравенства и его решение.
x 2 − 3x + 2 3 2 − 4 · 1 · 2
x1;2 =
| 3 ± √ 9 − 8 |
| 2 |
Рассмотрим другой пример квадратного неравенства и его решения.
x1;2 =
| 2 ± √ 2 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| 2 ± √ 4 + 12 |
| 2 |
В ответе неравенства мы получили два интервала в области решений
(x ≤ −1; x ≥ 3) и оба интервала нужно записать в ответ. Запись ответа неравенства всегда делается слева направо (как мы привыкли читать).
Начнем слева направо записывать интервалы в ответ. Первый интервал начинается с «минус» бесконечности и заканчивается на « −1 » (включительно). Так и запишем.
Второй интервал начинается с « 2 »(включительно) и заканчивается на «плюс» бесконечности. Для объединения интервалов используем знак « ∪ » («объединение»).
Метод интервалов: случай нестрогих неравенств
Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:
— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:
В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.
Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Задача. Решите строгое неравенство:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Задача. Решите нестрогое неравенство:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Почему бесконечности всегда стоят в круглых скобках
У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем
Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.
— это гипотетическое число, которое больше любого другого числа, участвующего в решении.
Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.
Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.
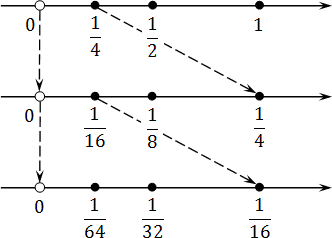
Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:
Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.
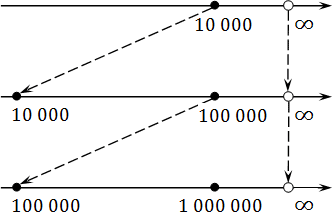
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:
Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.
Примеры решения неравенств
В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.
Как обычно, приравниваем все к нулю:
( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.
Теперь рассматриваем функцию, которая находится в левой части неравенства:
Подставим в эту функцию бесконечность — получим выражение вида:
Чертим координатную ось, отмечаем корни и расставляем знаки:
Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:
x (12 − 2 x )(3 x + 9) ≥ 0
x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.
x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.