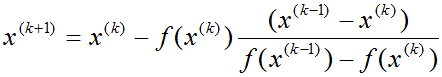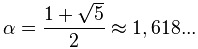Что общего у метода хорд и метода итераций
Что общего у метода хорд и метода итераций
Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что 
. По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |xn – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 
и нахождение участков возрастания и убывания функции.
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
X1=
= 0.268;
X2=
= 3.732;
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для второго корня отрезок [1, 3]:
Сравнение методов решения нелинейных уравнений
Метод половинного деления очень прост и имеет одно явное преимущество по сравнению со всеми рассмотренными выше методами – он всегда сходится. Однако, скорость сходимости очень мала, поэтому его часто используют для грубого уточнения корня.
Метод касательных (метод Ньютона) эффективен для решения уравнений, график которых в окрестности корня имеет большую крутизну. Метод обладает высокой скоростью сходимости, но его сходимость зависит от вида функции, поэтому рекомендуется отрезок, на котором отделяется корень, выбирать очень небольшой длины.
Метод хорд, являясь модификацией метода касательных, также обладает хорошей скоростью сходимости. При правильном выборе неподвижной точки последовательность приближений гарантированно сходится к корню уравнения.
Метод простой итерации дает возможность «угадывать» новые значения х на любом шаге. Следовательно, если процесс сходится медленно, можно вносить коррективы, учитывая предыдущие результаты. Метод прост и обладает хорошей сходимостью. Однако перед его использованием требуется преобразование исходного уравнения и проведение дополнительных вычислений.
Отметим, что на практике при решении нелинейных уравнений обычно используется комбинация нескольких методов.
Технология решения нелинейных уравнений средствами математических пакетов
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Метод хорд
Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.
Метод хорд (то же, что метод секущих) – итерационный метод решения нелинейного уравнения.
Нелинейное уравнение – это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.
Метод хорд. Алгоритм
Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.
Итерационная формула для вычислений методом хорд следующая:
Вычисления продолжаются до тех пор, пока не станет истинным выражение:
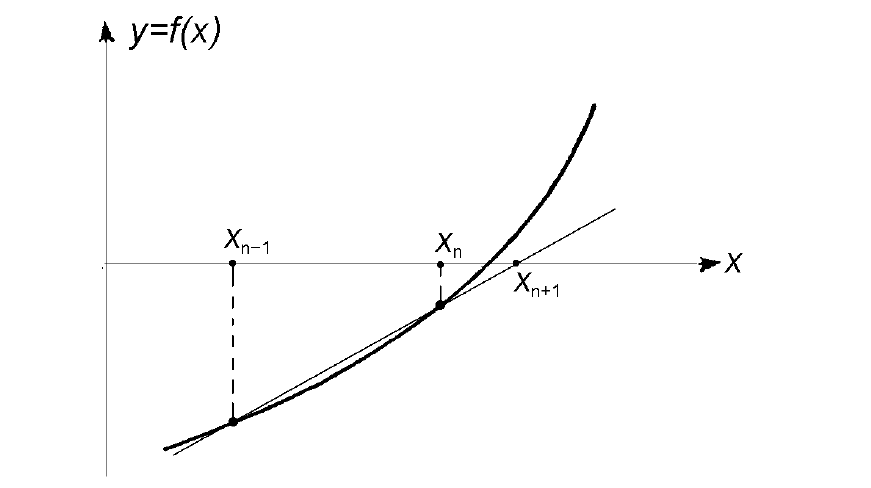
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:
Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:
Метод хорд. Программная реализация
Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.
В качестве примера ищется корень уравнения x 3 – 18x – 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).
x_prev – это xk-1, x_curr – это xk, x_next – это xk+1.
Вычислительная математика копия 1
Уравнение называется алгебраическим, если его можно представить в виде:
Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.
Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.
1.1 Отделение корня
Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.
Корень можно отделить аналитически и графически.
Графический метод отделения корня
1.2 Уточнение корня методом деления отрезка пополам
Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.
1.3 Метод хорд
Численные методы. Тесты численные методы с ответами
d) суммой векторов e) сходимостью векторного пространства
59) Максимальное число линейно независимых векторов n-мерного пространства Еn в точности равно a) размерности этого пространства b) соразмерности векторов c) сумме линейных векторов d) совокупности единичных векторов e) сумме n векторов
60) Название любой совокупности n линейно независимых векторов n-мерного пространства a) базис b) орт c) вектор d) координата e) скаляр
61) Как иначе называют метод бисекций?
a) Метод половинного деления b) Метод хорд c) Метод пропорциональных частей d) Метод «начального отрезка»
e) Метод коллокации
62) Методы решения уравнений делятся на:
a) Прямые и итеративные b) Прямые и косвенные
c) Начальные и конечные d) Определенные и неопределенные e) Простые и сложные
63) Кто опубликовал формулу для решения кубического уравнения?
a) Кардано b) Галуа c) Абеле d) Дарбу e) Фредгольм
64) Основная теорема алгебры:
a) Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k- кратный корень считать за k корней b) Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
c) Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке d) Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке e) Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения
65) Отделение корней можно выполнить двумя способами:
a) аналитическим и графическим b) приближением и отделением c) аналитическим и систематическим d) систематическим и графическим e) приближением последовательным и параллельным
b) Частный случай метода коллокации c) Частный случай метода прогонки d) Частный случай метода квадратных корней e) Частный случай метода Гаусса
75) Свойство самоисправляемости:
a) Усиливает надежность метода b) Не влияет на конечный результат c) Влияет на конечный результат d) Не учитывается e) Считается ошибочным
76) Как иначе называют метод Ньютона?
a) Метод касательных b) Метод коллокации c) Метод прогонки d) Метод итераций e) Метод хорд
77) Как иначе называют метод хорд?
a) Метод пропорциональных частей b) Метод касательных c) Метод коллокации d) Метод бисекций e) Метод квадратных корней
78) Метод хорд имеет еще одно имя:
a) Метод пропорциональных частей b) Метод касательных c) Метод бисекций d) Метод коллокации e) Метод прогонки
79) Что общего у метода хорд и метода итераций?
a) Общая скорость и свойство самоисправляемости b) Свойство самоисправляемости c) Общая скорость d) Легкость при решении e) Требуется нахождение производной
80) Метод Ньютона- a) обладает свойством самоисправляемости и имеет высокую скорость сходимости b) дает большой выигрыш во времени c) занимает очень много времени d) предельно прост e) надежен
81) Методом хорд уточнить корень уравнения х3 – 2х – 3=0, ξ[1;2]; ε=10-3
a) ξ=1.8933±0.0001
b) ξ=0.0001±1
c) ξ=0.0033±0.0001
d) ξ=±1
e) ξ=±3.3