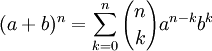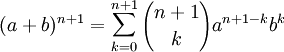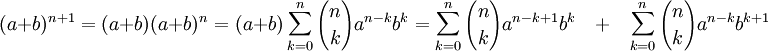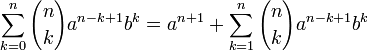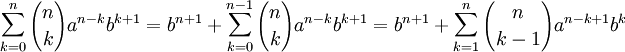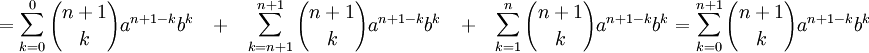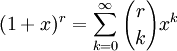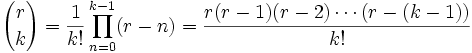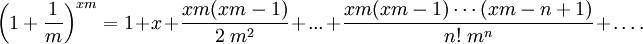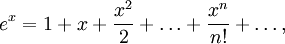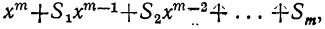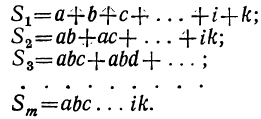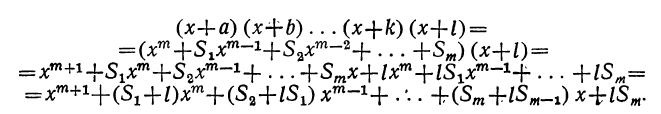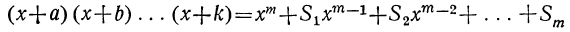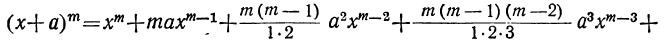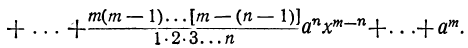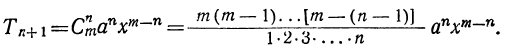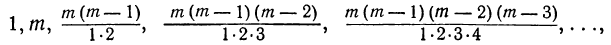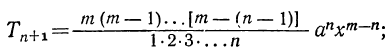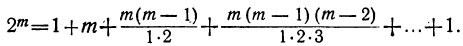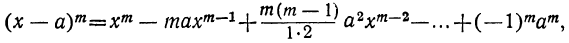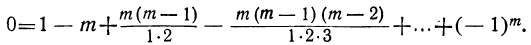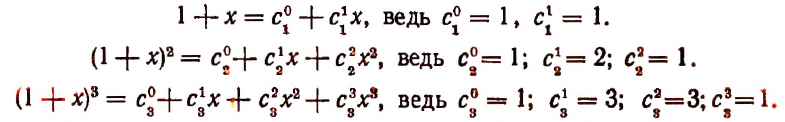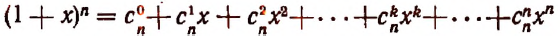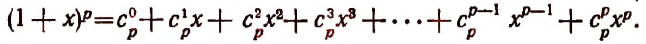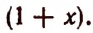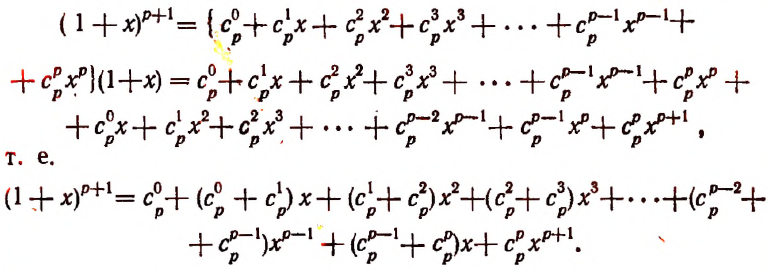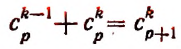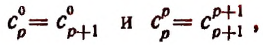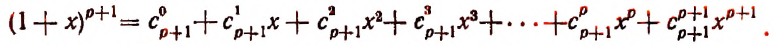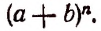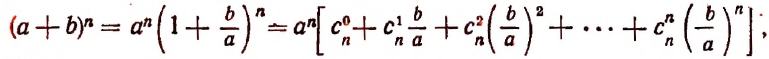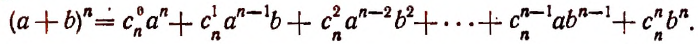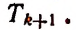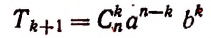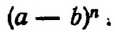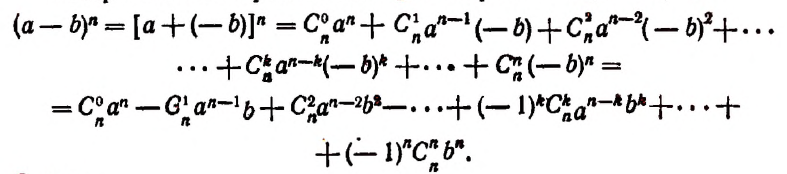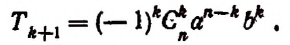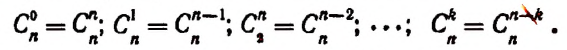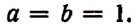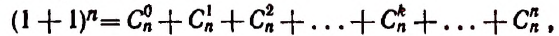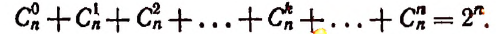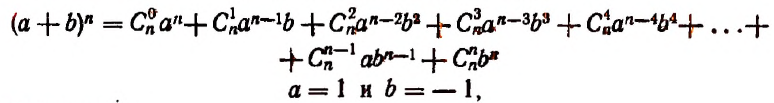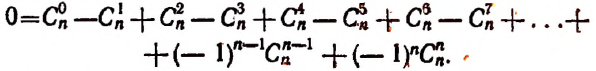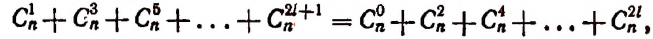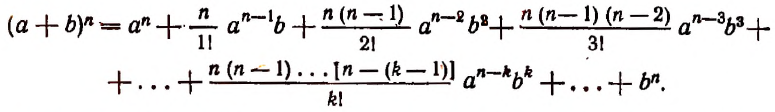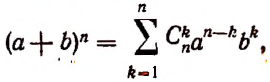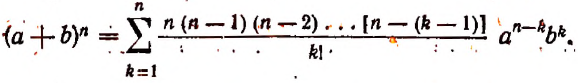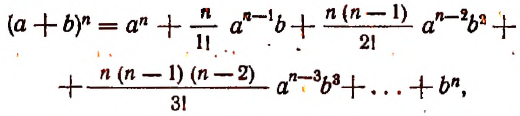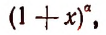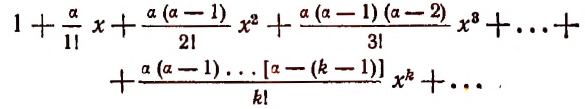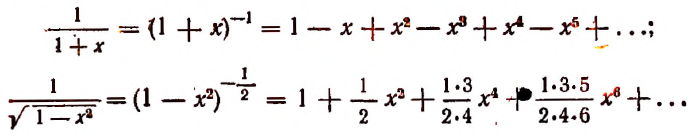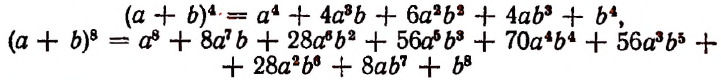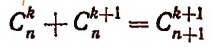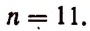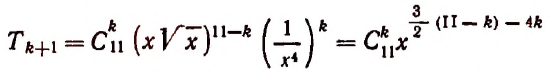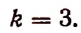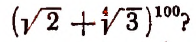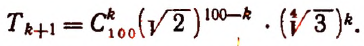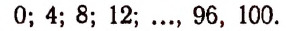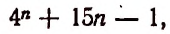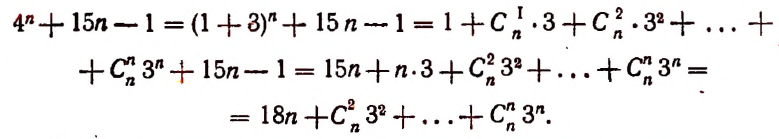Что означает c в биноме ньютона
Бином ньютона
Бином Ньютона — это формула
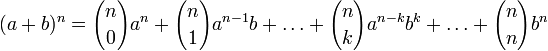
где 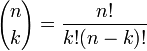
Содержание
Доказательство
Докажем это равенство, используя метод математической индукции:
Пусть утверждение для n верно:
Тогда надо доказать утверждение для n + 1 :
Извлечём из первой суммы слагаемое при k = 0
Извлечём из второй суммы слагаемое при k = n
Теперь сложим преобразованные суммы:
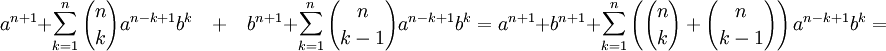
Что и требовалось доказать
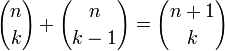
Для ненатуральных степеней
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты находятся по формуле:
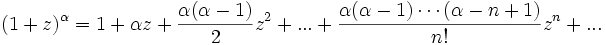
сходится при 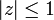
В частности, при 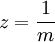
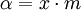
Переходя к пределу при 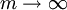
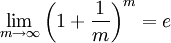
именно таким образом впервые полученное Эйлером.
История
Считается, что эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Тем не менее, она была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке. Возможно, её открыл персидский учёный, поэт и философ Омар Хайям.
Исаак Ньютон обобщил формулу для прочих показателей степени.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.
Об этой специфической роли бинома Ньютона в культуре писал известный математик В. А. Успенский [1].
См. также
Полезное
Смотреть что такое «Бином ньютона» в других словарях:
бином ньютона — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго
БИНОМ НЬЮТОНА — БИНОМ НЬЮТОНА, математическое правило разложения алгебраического выражения (а+b)n в ряд степеней численных значений х и у (где n положительное число). При n 2 разложение выглядит таким образом: (х+у)2=х2+2ху+у2 … Научно-технический энциклопедический словарь
Бином Ньютона — алгебраическая формула, открытая Ньютоном, выражающая какую угодно степень двучлена, а именно: (х + а)n = хn + n/1(axn 1) + [n/(n 1)/1.2](а2хn 2) + …[n(n 1)(n 2)…(n m+1)/1.2.3…m](anxn m) + … или, в компактной форме, пользуясь символом n! =… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Бином Ньютона — Разг. Шутл. О чём л. сложном, запутанном. Елистратов, 41 … Большой словарь русских поговорок
Подумаешь, бином Ньютона! — Из романа (гл. 18 «Неудачливые визитеры») «Мастер и Маргарита» (1940) Михаила Афанасьевича Булгакова (1891 1940). Слова Коровьева Фагота, комментирующего диалог между Воландом и буфетчиком Андреем Фокичем Соковым. Последний пришел жаловаться на… … Словарь крылатых слов и выражений
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
БИНОМ — (от лат. bis дважды, и греч. nomos часть, отдел). Двучлен (в алгебре). Бином Ньютона общая формула для возведения двучленного количества в любую степень. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИНОМ в… … Словарь иностранных слов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
Древние знания
Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.
Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.
Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.
Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.
Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:
К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.
Утверждение теоремы
Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.
Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :
Теорема может быть применена к степеням любого бинома.
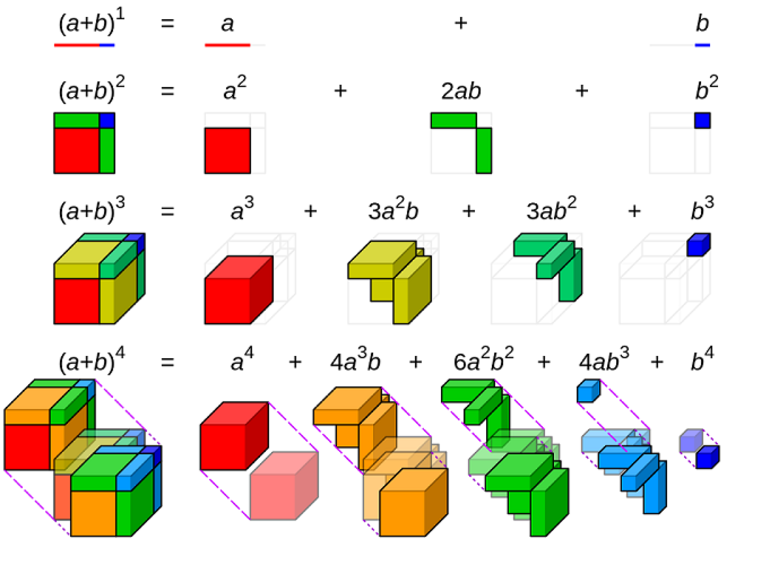
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Биномные обобщения
Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
Короткий путь
Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.
Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).
Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.
Что означает c в биноме ньютона
Бином Ньютона
Автор работы награжден дипломом победителя II степени
Формула бинома Ньютона для целых положительных показателей была известна задолго до Исаака Ньютона, но он в 1676 году указал на возможность распространения этого разложения и на случай дробного или отрицательного показателя. Строгое обоснование указанных Ньютоном возможностей дал Н. Абель в 1826 году. В случае дробного или отрицательного n все биномиальные коэффициенты отличны от нуля, а правая часть формулы получает бесконечный ряд членов (биномиальный ряд). Бином Ньютона играет роль во многих областях математики, в частности в алгебре и теории чисел.
Бином Ньютона — формула разложения произвольной натуральной степени двучлена ( a + b ) n в многочлен. Каждый из нас знает наизусть формулы «квадрата суммы» ( a + b )2 и «куба суммы» ( a + b )3,но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности, которые я рассматриваю в своей работе.
3. История бинома Ньютона
5. Свойства разложения бинома Ньютона
6. Решение задач с применением бинома Ньютона
8. Список используемой литературы
Изучить бином Ньютона и его свойства
Показать применение данных свойств при решении задач
Показать применение бинома Ньютона при решении технических задач
История бинома Ньютона
Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю (англ.), жившему в XIII веке, а также исламским математикам ат-Туси (XIII век) и ал-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.
Исаак Ньютон около 1677 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.
Что означает фразеологизм «Бином Ньютона»?
Шутливая фраза, применяется по отношению к плевому делу, простой задаче, которую некоторые ошибочно считают непосильной для выполнения или архисложной.
Слова Коровьева, которые решил прокомментировать разговор Воланда с буфетчиком Соковым. Буфетчик жалуется на зрителей, которые расплатились с ним фальшивыми деньгами, чем «на сто девять рублей наказали буфет».
Тут уж буфетчик возмутился.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.
В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о математике профессоре Мориарти:
Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая карьера.
В романе «Мастер и Маргарита» М. А. Булгакова:
«подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
Позже это же выражение «Подумаешь, бином Ньютона!». упомянуто в фильме «Сталкер» А. А. Тарковского.
Роман Е. Н. Вильмонт получил название «Мимолетности, или Подумаешь, бином Ньютона!».
Рассмотрим произведения двух, трех и четырех биномов (двучленов) вида х-<- а. После умножения и приведения подобных членов по х получим
Рассматривая эти произведения, легко заметить, что произведение биномов, отличающихся только вторыми членами, есть многочлен, упорядоченный по убывающим степеням первого члена х, степень которого равна числу перемножаемых биномов. Коэффициент первого члена многочлена равен 1, а последующие образуются так: второй коэффициент равен сумме всех вторых членов биномов, третий — сумме всевозможных произведений вторых членов по два, четвертый — сумме всевозможных произведений вторых членов по три и т. д. 11оследний член многочлена равен произведению всех вторых членов биномов.
Методом математической индукции можно доказать, что правило образования произведения биномов, отличающихся только вторыми членами, установленное из рассмотрения произведений двух, трех II четырех биномов, верно для произведения любого конечного числа биномов.
Для произведения n биномов справедлива формула:
Эта формула верна и в том случае, если вторые члены равны между собой.
(x+a) n =x n +C 1 n ax n-1 +…+C k n a k x n-k +…+C n-1 n a n-1 x+a n
Свойства разложения бинома Ньютона
1) Количество членов разложения бинома на единицу больше показателя степени бинома.
2) Все члены разложения имеют одну и ту же степень n относительно первого и второго членов бинома, т. е. разложение есть однородный многочлен, причем показатели первого члена убывают от n до 0, а показатели второго члена возрастают от 0 до п.
5) Из свойств 1 и 4 следует, что если показатель бинома четный, то в разложении бинома средний член имеет наибольший биномиальный коэффициент, а если показатель бинома нечетный, то в разложении имеется два средних члена с одинаковым наибольшим коэффициентом.
6) Последующий биномиальный коэффициент разложения равен предыдущему, умноженному на показатель первого члена бинома и предыдущем члене и деленному на число предыдущих членов
Сумма всех биномиальных коэффициентов равна 2 п , где п — показатель бинома.
Если в формуле бинома Ньютона положить х = а = 1, то получим
Если в формуле бинома Ньютона заменить а на -а, то получим
Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах.
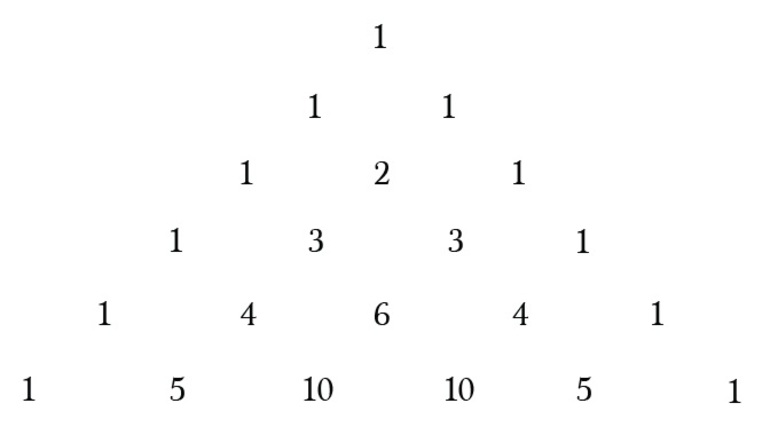
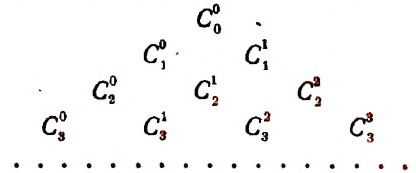
Для определения биномиальных коэффициентов удобно пользоваться так называемым треугольником Паскаля или арифметическим треугольником. Это треугольная таблица биномиальных коэффициентов, составленная так, что каждый ее элемент равен сумме двух над ним стоящих.
Решение задач с применением бинома Ньютона
Возведите в степень: (2t + 3/t)4.
Решение У нас есть (a + b)n, где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:
Пример 5 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:
Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?
Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно
Таким образом, Венди может предложить 512 различных гамбургеров.
Решение технических задач
Тяга воздушного винта и потребляемая им мощность вычисляются по формулам: P = apn 2 s D 4 N = bpn 3 s D 5
Определить, на сколько снизилась тяга этого винта и потребляемая им Мощность при тех же секундных оборотах, если полагать все остальные параметры, входящие в формулы, неизменными.
откуда ∆ T = T 1[1- 1/(1+∆ Q / Q 1) 9 ]= T 1[1-1/1+9∆ Q / Q 1+36(∆ Q / Q 1) 2 +82(∆ Q / Q 1) 3 +126(∆ Q / Q 1) 4 +126(∆ Q / Q 1) 5 +82(∆ Q / Q 1) 6 +36(∆ Q / Q 1) 7 +9(∆ Q / Q 1) 8 +(∆ Q / Q 1) 9 ]
Если ∆ Q / Q 1 Q / Q 1 выше первой очень малы. В Этом случае ∆ T ≈ T 1(1-1/1+9∆ Q / Q 1)= 9 T 1 *∆ Q / Q 1 /1+9∆ Q / Q 1
Газ сжимается в сосуде, стенки которого хорошо проводят тепло. При этом абсолютная температура и давление газа связаны следующим уравнением:
где п= 1,2—показатель политропы; р1 и р2 — соответственно давления первого и второго состояния; T 1и T 2— соответственно абсолютные температуры первого и второго состояния.
Температура в сосуде измеряется посредством помещенной в нем термопары. Пусть во втором состоянии при сжатии температура получила небольшое приращение ∆ t = 5° против первого состояния. Определить, какое приращение получило при этом давление. Температура Т1 = 300° и давление р1 = 2 кГ/см 2 — первого состояния известны.
Подставляя значения T 2и p 2 в формулу, получаем:
откуда ∆ T = T 1[1- 1/(1+∆ Q / Q 1) 9 ]= T 1[1-1/1+9∆ Q / Q 1+36(∆ Q / Q 1) 2 +82(∆ Q / Q 1) 3 +126(∆ Q / Q 1) 4 +126(∆ Q / Q 1) 5 +82(∆ Q / Q 1) 6 +36(∆ Q / Q 1) 7 +9(∆ Q / Q 1) 8 +(∆ Q / Q 1) 9 ]
Если ∆ Q / Q 1 Q / Q 1 выше первой очень малы. В Этом случае ∆ T ≈ T 1(1-1/1+9∆ Q / Q 1)= 9 T 1 *∆ Q / Q 1 /1+9∆ Q / Q 1
где Q —вес поднимаемого груза; k = 1,02 — коэффициент сопротивления блока; n — число ветвей полиспаста. Вывести упрощенную формулу для вычисления Р и, применив ее, определить Р, если Q = 1500 кГ и п = 5.
Заметим, что 0.02 2 =0.0004; 0.02 3 =0.000008 и т.д.
Видно, что члены разложения по формуле Ньютона быстро убывают. Для практики достаточно учесть первые 3 числа разложения, пренебрегая следующими. Тогда получаем:
Для нас получаем : P =1.02 5 *1500/5[1+(5-1)*0.01]≈ 318 кГ
При изучении математики решение задач играет огромную роль. И не только потому,что необходимо выработать умение применять полученные знания на практике (а ведь это одна из основных целей изучения математики в школе). Без решения задач нельзя владеть и теорией. Именно в процессе решения задач математические понятия, аксиомы и теоремы, формулы и правила, геометрические фигуры предстают перед нами в самых разнообразных ракурсах, не в застывшем виде, а в движении, в различных связях и взаимозависимостях, которые отображают диалектику самой действительности. Подобно тому, как грамматическими правилами можно овладеть лишь в процессе живой языковой практики, так и математическую теорему, определение, формулу можно усвоить по-настоящему, научиться применять на практике только в процессе решения задач.
1. А.Б. Шкарин, А.М. Федянов, Б.Г. Сандлер «алгебраические задачи в технике»
2. А.П. Савин «Энциклопедический словарь»
3. Г.И. Глейзер «История математики в школе»
4. Ф.П. Яремчук, П.А. Рудченко «Алгебра и элементарные функции»
Бином Ньютона — математическая формула с примером решения и объяснением
Рассматривая эти произведения, замечаем, что все они составлены по одному и тому же закону, а именно:
Произведение составляет многочлен, расположенный по убывающим степеням буквы х.
Показатель первого члена равен числу перемножаемых биномов; показатели при х в следующих членах убывают на 1; последний член не содержит х (содержит его в нулевой степени).
Коэффициент первого члена есть 1; коэффициент второго члена есть сумма всех вторых членов перемножаемых биномов; коэффициент третьего члена есть сумма всех произведений вторых членов, взятых по два; коэффициент четвёртого члена есть сумма всех произведений вторых членов, взятых по три. Последний член есть произведение всех вторых членов.
Итак, допустим, что верно следующее равенство:
(x+α) (x+b) (х+с)… (x+k) =
где для краткости мы положим:
Умножим обе части допущенного равенства на бином x+l:
Рассматривая это новое произведение, убеждаемся, что оно подчиняется такому же закону, какой мы предположили верным для m биномов. Действительно, во-первых, этому закону следуют показатели буквы х; во-вторых, ему же следуют и коэффициенты, так как коэффициент второго члена S+l есть сумма всех вторых членов перемножаемых биномов, включая сюда и l; коэффициент третьего члена S₂+lS₁ есть сумма парных произведений всех вторых членов, включая сюда и l, и т. д.; наконец, 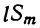
Мы видели, что закон этот верен для произведения двух, трёх и четырёх биномов; следовательно, по доказанному теперь, он должен быть верен и для произведения 4+1, т. е. для произведения пяти биномов, если же он верен для произведения пяти биномов, то он верен и для произведения 5+1, т. е. для произведения шести биномов, и т. д.
Формула бинома Ньютона
Предположим, что в доказанном нами равенстве
все вторые члены биномов одинаковы, т. е. что a=b=c= … =k. Тогда левая часть будет степень бинома 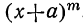
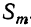
Коэффициент S₁, равный a+b+c+ … +k, обратится в та. Коэффициент S₂, равный ab+ac+ad+ …. обратится в число α², повторённое столько раз, сколько можно составить сочетаний из m элементов по 2, т. е. обратится в 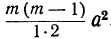
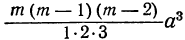
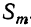
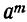
Это равенство известно как формула бинома Ньютона, причём многочлен, стоящий в правой части формулы, называется разложением бинома. Рассмотрим особенности этого многочлена.
Свойства формулы бинома Ньютона
Из этих свойств мы укажем следующие 10:
1) Показатели буквы х уменьшаются на 1 от первого члена к последнему, причём в первом члене показатель х равен показателю степени бинома, а в последнем он есть 0; наоборот, показатели буквы а увеличиваются на 1 от первого члена к последнему, причём в первом члене показатель при а есть 0; а в последнем он равен показателю степени бинома. Вследствие этого сумма показателей при х и а в каждом члене одна и та же, а именно: она равна показателю степени бинома.
2) Число всех членов разложения есть m+1, так как разложение содержит все степени а от 0 до m включительно.
3) Коэффициенты равны: у первого члена — единице, у второго члена — показателю степени бинома, у третьего члена — числу сочетаний из m элементов по 2, у четвёртого члена — числу сочетаний из m элементов по 3; вообще коэффициент (n+1)-ro члена есть число сочетаний из m элементов по n. Наконец, коэффициент последнего члена равен числу сочетаний из т элементов по m, т. е. 1.
Заметим, что эти коэффициенты называются биномиальными.
4) Обозначая каждый член разложения буквой T с цифрой внизу, указывающей номер места этого члена в разложении, т. е. первый член T₁, второй член T₂ и т. д., мы можем написать:
Эта формула выражает общий член разложения, так как из неё мы можем получить все члены (кроме первого), подставляя на место n числа: 1, 2, 3,…. m.
5) Коэффициент первого члена от начала разложения равен единице, коэффициент первого члена от конца тоже равен единице. Коэффициент второго члена от начала есть m, т. е. 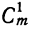
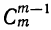
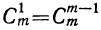
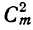
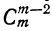
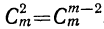
Коэффициенты членов, одинаково удалённых от концов разложения, равны между собой.
6) Рассматривая биномиальные коэффициенты:
мы замечаем, что при переходе от одного коэффициента к следующему числители умножаются на числа, всё меньшие и меньшие (на m—1, на m — 2, на m — 3 и т. д.), а знаменатели умножаются на числа, всё большие и большие (на 2, на 3, на 4 и т. д.). Вследствие этого коэффициенты сначала возрастают (пока множители в числителе остаются большими соответственных множителей в знаменателе), а затем убывают. Так как коэффициенты членов, равно отстоящих от концов разложения, одинаковы, то наибольший коэффициент должен находиться посередине разложения. При этом, если число всех членов разложения нечётное (что бывает при чётном показателе бинома), то посередине будет один член с наибольшим коэффициентом; если же число всех членов чётное (что бывает при нечётном показателе бинома), то посередине должны быть два члена с одинаковыми наибольшими коэффициентами. Например:
(х+α)⁴=x⁴+4αx³+6α²x²+4α³x+α⁴;
(x+α)⁵=x⁵+5αx⁴+10α²x3+10α³x²+5α⁴x+α⁵∙
7) Из сравнения двух рядом стоящих членов: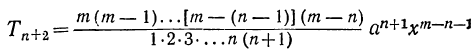
заключаем, что:
Для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы х в этом члене и разделить на число членов, предшествующих определяемому.
Пользуясь этим свойством, можно сразу писать, например, (x+a)⁷=x⁷+7ax⁶+…
Теперь уже выписаны члены до середины ряда, остальные получим, основываясь на свойстве пятом:
(х+а)⁷ =х⁷-7αx⁶+21α²x⁵+35α³x⁴+35α⁴x³+21α⁵x²+7α⁶x+α⁷.
8) Сумма всех биномиальных коэффициентов равна 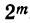
Например, сумма коэффициентов в разложении (х+a)⁷ равна
1+7+21+35+35 +21+7+1 = 128=2⁷.
9) Заменив в формуле бинома а на — а, получим: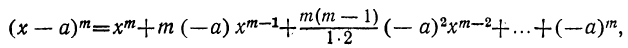
т. е.
следовательно, знаки + и — чередуются.
10) Если в последнем равенстве положим x=α =1, то найдём:
Сумма биномиальных коэффициентов, стоящих на нечётных местах, равна сумме биномиальных коэффициентов, стоящих на чётных местах.
Применение формулы бинома к многочлену
Формула бинома Ньютона позволяет возвышать в степень многочлен. Так:
(α+ b+c)⁴ = [(а+b)+с]⁴= (a+b)⁴+4c (а+b)³+6c² (а+b)²+4c³ (a+b)+c⁴.
Вывод формулы бинома ньютона
Возникает вопрос, будет ли закономерность, наблюдаемая в этих формулах, обладать общностью, т. е. будет ли справедливой формула
при всяком натуральном значении n?
Воспользуемся методом полной индукции. Допустим, что формула верна для произвольно взятого натурального числа р, т. е. предположим справедливым следующее равенство:
Умножим обе части этого предполагаемого равенства на
и приняв во внимание, что
Из предположения, что формула верна при 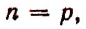
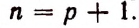
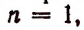
Теперь легко получить разложение и для
Последняя формула и называется формулой бинома Ньютона. Ее правая часть называется разложением степени бинома.
Числа 
Свойства разложения бинома
В разложении бинома содержится членов на один больше, чем показатель степени бинома.
Все члены разложения имеют относительно букв а и b одно и то же измерение, равное показателю степени бинома. (Измерением одночлена относительно букв а и b называется сумма показателей степеней этих букв, входящих в этот одночлен.)
Поскольку все члены разложения имеют одинаковое измерение относительно букв а и b, то это разложение является однородным многочленом относительно букв а и b (см. стр. 450).
В разложении показатель степени буквы а последовательно понижается на единицу, начиная с показателя n, а показатель степени буквы b последовательно повышается на единицу, начиная с показателя, равного нулю.
Член разложения 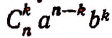
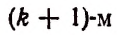
называется формулой общего члена разложения, так как, давая букве k целые значения от 0 до n, мы можем получить из нее любой член разложения.
Теперь напишем разложение для выражения
Свойства биномиальных коэффициентов
1. Биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны между собой. Действительно, по первому свойству числа сочетаний имеем:
2. Сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома.
Доказательство:
Положим, в формуле бинома
3. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме, биномиальных коэффициентов, стоящих на нечетных местах.
Доказательство:
Полагая в тождестве
Перенеся все отрицательные члены в левую часть, получим:
что и требовалось доказать.
Если вместо биномиальных коэффициентов 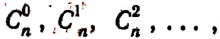

Формулу бинома Ньютона принято записывать ради краткости в следующем символическом виде:
Читателю может показаться непонятным, почему столь элементарная формула
где n — целое положительное число, носит имя великого ученого Ньютона, тем более что эта формула была известна до Ньютона. Например, ее знал Аль-Каши (XV век) и она встречается в трудах Паскаля. Объясняется это тем, что именно Ньютоном была обобщена эта формула для любого действительного показателя.
Ньютон впервые показал, что выражение
где 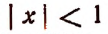
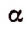
Например, если 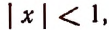
Арифметический треугольник, или треугольник паскаля
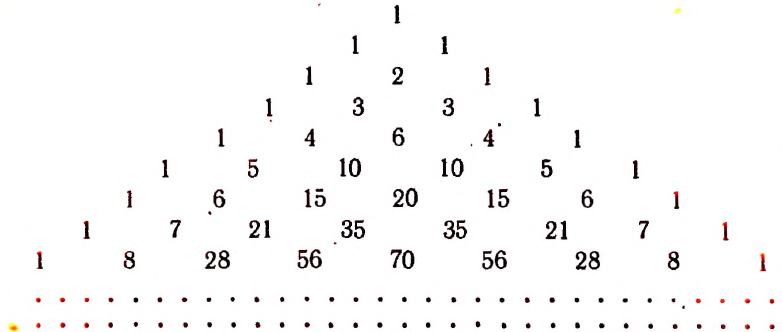
Написанная ниже таблица
называется треугольником Паскаля *.
По боковым сторонам этой таблицы стоят единицы, внутри же стоят числа, получающиеся сложением двух соответствующих чисел предыдущей строки. Например, число 21 в 8-й строке получается сложением стоящих над ним чисел 6 и 15.
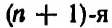
Треугольник Паскаля получается из следующей таблицы:
Треугольник Паскаля приведен в книге Паскаля «Трактат об арифметическом треугольнике», изданной после его смерти в 1665 году.
Примеры с решением на Бином Ньютона
1. В разложении 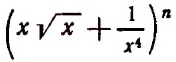
Решение:
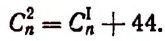
Приравняв показатель степени буквы х к нулю, получим:
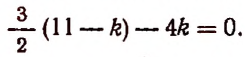
Искомым свободным членом будет четвертый, и он будет равен 
2. Сколько рациональных членов содержится в разложении
Решение:
Для рациональности члена разложения необходимо, чтобы число k было кратно четырем. Но тогда 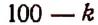
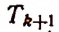
Число k может принимать целые значения 0, 1, 2….. 100. Среди этих чисел кратными четырем будут
Пользуясь формулой 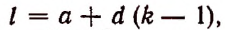
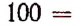
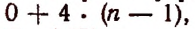

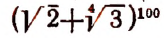
3. Доказать, что значение выражения
где n — натуральное число, делится на 9.
Доказательство:
Каждое слагаемое последней суммы делится на 9, следовательно, и вся эта сумма, т. е. значение выражения 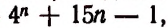
Дополнение к Бином Ньютону
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института