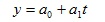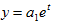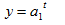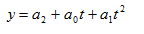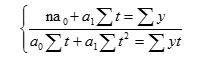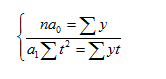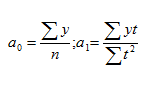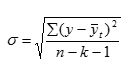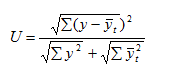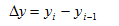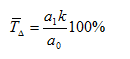Что означает динамический ряд для чего используют динамические ряды

Ряды динамики

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».

В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.

Год	y					, %	,%
2004	144,2
2005	143,5	-0,7	-0,7	0,995	0,995	-0,49	-0,49
2006	142,8	-1,4	-0,7	0,990	0,995	-0,97	-0,49
2007	142,2	-2,0	-0,6	0,986	0,996	-1,39	-0,42
2008	142,0	-2,2	-0,2	0,985	0,999	-1,53	-0,14
2009	141,9	-2,3	-0,1	0,984	0,999	-1,60	-0,07
Итого	-2,3	0,984	-1,60

Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

.

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле

Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.

Источник

Ряды динамики в статистике

Ряд динамики может состоять из:

Виды рядов динамики

Объединение радов происходит по:

Чтобы без ошибок построить динамические ряды, необходимо сопоставлять уровни рядов разных периодов. Для этого у них должны быть однородные величины. Также ряды предполагают охват явления с одинаковой полнотой.

Не допускать погрешностей в анализе динамики помогает смыкание рядов динамики. Суть понятия в проведении подготовительной работы до основных расчетов. Во время подготовки ряды объединяются в один. Уровни этих рядов рассчитаны по разным методологиям. Смыкание также включает преобразования, при которых абсолютные уровни рядов приводятся к общему основанию. Это действие помогает избежать несопоставимости уровней.

Анализ показателей в рядах динамики

Ряд динамики характеризует изменения данных внутри этого ряда. Статистические данные необходимо сравнивать также между рядами. По формулам можно определить основные показатели.

Разность уровней ряда динамики называется абсолютным приростом. Показатель демонстрирует, на сколько изменился каждый последующий уровень.

Отношение уровней ряда динамики называется темпом (коэффициентом) роста. По нему видно, во сколько раз изменились последовательные значения.

Темп прироста. Показывает процентное отличие между последовательными уровнями.

Если сравнивать между собой числа без всякой системы, не получится грамотно проанализировать ситуацию и выстроить новую стратегию. Например, продвижение продукта на основе маркетинговой стратегии. Использование формул поможет высчитать, какую прибыль принесло компании конкретное решение за анализируемый период.

Анализ показателей за длительный промежуток

Если есть задача оценить изменения, которые касаются длинного временного отрезка, эффективно применить средние показатели. В статистике для их определения используются следующие понятия.

Средний уровень ряда динамики. Применим для интервальных равноотстоящих рядов

Если ряды неравноотстоящие, средний уровень интервального ряда динамики определяется как

Использование перечисленных методов позволяет применять полученные значения в экономике. Определять эффективность финансовых вложений, прогнозировать результаты. В управление предприятиями и бухгалтерию также можно внедрить данные методы для планирования и распределения бюджета.

Источник

Динамический ряд, уровни, виды. Показатели динамического ряда. Выравнивание динамического ряда

Динамический ряд – это ряд статистических однородных величин, показывающих изменение какого-то явления в последовательные периоды времени. Его называют также хронологическим.

Числа, составляющие динамический ряд, являются уровнями динамического ряда.

Ряды могут быть простыми и сложными. В простых рядах уровни ряда представлены абсолютными величинами. Различают два вида простых рядов: интервальный и моментный.

Интервальный ряд состоит из последовательного ряда уровней, характеризующих изменение явления за определенный интервал времени.

Моментный ряд представлен уровнями, определяющими размеры явления на определенную дату (момент).

Сложный динамический ряд формируется из относительных или средних величин (уровней).

Динамический ряд характеризуют следующие показатели:

– абсолютный прирост (убыль) ряда (показывает разность между последующим и предыдущим уровнем динамического ряда);

– темп прироста или снижения (выражает отношение абсолютного прироста к предыдущему уровню динамического ряда в % и показывает, на сколько процентов увеличился (снизился) последующий уровень, по сравнению с предыдущим);

– абсолютное значение 1 % прироста или убыли (выражает отношение абсолютного прироста к темпу прироста);

– темп роста(представляет процентное отношение последующего уровня к предыдущему уровню);

– показатель наглядности (показывает отношение каждого уровня ряда к одному из них, чаще начальному, принятому за 100%).

С целью выявления основных закономерностей, свойственных явлению за наблюдаемый период, применяют следующие методы выравнивания динамического ряда:

– укрупнение ряда (суммирование данных соседних периодов);

– расчет групповой средней – определение средней величины каждого укрупненного периода (интервала);

– расчет скользящей средней (каждый уровень ряда заменяется на среднюю из данного уровня и двух соседних с ним);

Рассмотрим пример выравнивания динамического ряда по методу укрупнения интервалов (столбец 3) и сглаживания ряда методом групповой скользящей средней (столбцы 4, 5 и 6): ₃

1. Проводим группировку по трем периодам наблюдения (∑Хi).

2. Рассчитываем среднюю по укрупненным интервалам (Х).

3. Проводим группировку с отступом на один показатель (1,2,3;2,3,4;3,4,5 и т.д.). ₃

Вычисляем Y_i+1по следующей формуле: Y_i+1 = (∑Хi).

Например: Y₂ = 3,5+2,8+3,6;Y₃ = 2,8+3,6+3,7 и т.д.

4. Рассчитываем скользящую среднюю (`y), как (`y =∑Y_i+1/3)

Таблица 1.1 Исходные данные и результаты выравнивания динамического ряда

Источник

Динамические ряды — краткое руководство по анализу изменений явлений во времени

Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.

Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.

Целью анализа динамических рядов является:

Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).

Типы динамических рядов:

а) простые (уровень ряда выражен абсолютными числами);

б) сложные (уровень ряда выражен обобщающими коэффициентами).

а) моментные (данные собираются на определенный момент времени);

б) интервальные (данные собираются за определенный период времени).

а) с выраженной тенденцией (r =0,7 — 1,0);

б) с неустойчивой тенденцией (r =0,3 — 0,69);

в) с отсутствием тенденции ( r = 0 — 0,29).

Основное требование, предъявляемое к анализируемым динамическим ря­дам, заключается в сопоставимости их уровней. Для оценки сопоставимости прово­дят предварительный анализ полученных данных по следующим критериям:

Методика анализа динамических рядов

Методика аналитики предусматривает выполнение последовательных действий:

Способы выравнивания динамических рядов

Чтобы произвести выравнивание динамических рядов потребуются следующие действия:

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:

а) линейная зависимость:

б) экспоненциальная зависимость:

в) показательная зависимость:

г) параболическая зависимость:

у – теоретический уровень;

t – временной интервал.

где у — уровни фактического ряда;

n — количество уровней;

t — порядковый номер временного периода.

При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:

Отсюда находим параметры уравнения:

Подставляя в уравнение у = а₀ + а₁t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обуслов­лено как случайными колебаниями, так и неправильно подобранным аппроксими­рующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения

Для получения точной оценки необходимо найти такие величины:

а) коэффициент вариации:

где у- фактический уровень ряда;

y_t — теоретический уровень ряда;

k- число параметров уравнения;

n- число уровней ряда.

Аппроксимация считается точной при C_v не более 15%.

б) коэффициент расхождения Тейла:

где у — фактический уровень ряда;

y_t — теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факто­ров и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.

Вычисление основных показателей динамического ряда

Алгоритм вычислений ведущих параметров динамических рядов:

yi- текущий уровень (сравниваемый);

у_i-1— базисный уровень (с каким сравнивают);

t- период времени, в течение которого уровень предполагается неизменным.

1.Абсолютный прирост (убыль) :

3.Темп прироста (относительная скорость), темп убыли :

4.Средний темп прироста (убыли):

где а₀; а₁ — параметры уравнения;

k = 1 при нечетном ряде;

k = 2 при четном ряде.

5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.

Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!

Источник

Динамические ряды

Ряд расположенных в хронологической последовательности значений статистических показателей представляет собой временной (динамический) ряд.

Статистические показатели, характеризующие изучаемый объект, называют уровнями ряда. В динамическом ряду они могут быть абсолютными, относительными или средними величинами. Ряды динамики, представленные за определенный промежуток времени, называются интервальными. В результате суммирования уровней интервального динамического ряда получаем накопленные итоги. Вследствие многих обстоятельств однородность величин, составляющих динамический ряд, может нарушаться, и таким образом изменяется сопоставимость уровней динамического ряда. Если каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, как правило, первоначальным – это сравнение с первоначальной базой. Если сравнение проводится с предшествующим уровнем – это сравнение с переменной базой.

Для представления модели динамического ряда используется аналитическое выравнивание ряда динамики. Закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени. В табл. 10.1 приводятся различные виды трендовых моделей, наиболее часто используемые для аналитического выравнивания.

Выбор формы кривой определяет результаты экстраполяции тренда. Одним из наиболее распространенных приемов сглаживания уровней первоначального ряда динамики – это метод скользящей средней.

Выполнить прогноз по уравнению тренда можно путем экстраполяции тенденции, наблюдавшейся в прошлом. Уровень динамического ряда (ŷ), полученный в результате экстраполяции, используется для определения прогнозного значения на будущее.

Наличие зависимости между последующими и предшествующими уровнями динамического ряда называют автокорреляцией, а построение модели зависимости будущих значений рассматриваемого показателя от прошлых его значений называется авторегрессией.

Таблица 10.1 Виды трендовых моделей

Парабола второго порядка

Ŷ _t = b ₀ ∙ e Ŷ _t = b ₀ ∙ b Ŷ _t = Ŷ _t = Источник