Что означает длину отрезка

Длина отрезка

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

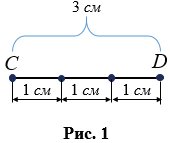
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

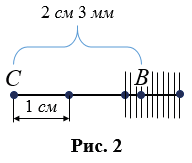
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

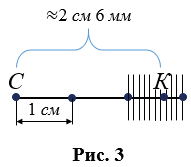
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Свойства длин отрезков:

Поделись с друзьями в социальных сетях:

Источник

ВОПРОСЫ

1. Сколько существует отрезков, концами которых являются две дан­ные точки?

2. Как обозначают отрезок?

3. Какие вы знаете единицы длины?

Нам известны такие единицы длины: миллиметр, сантиметр, дециметр, метр, километр.

4. Объясните, что означает измерить длину отрезка.

5. Каким свойством обладает длина отрезка?

6. Какие отрезки называют равными?

7. Какие длины имеют равные отрезки?

8. Какой из двух неравных отрезков считают большим?

9. Что называют расстоянием между точками А и В?

10. Объясните, какую геометрическую фигуру называют ломаной.

11. Что называют длиной ломаной?

12. Какую ломаную называют замкнутой?

РЕШАЕМ УСТНО

1. Какое число больше числа 46 на 9? Какое число меньше числа 72 на 15? Какое число больше числа 21 в 7 раз? Какое число меньше числа 65 в 13 раз?

2. Назовите все двузначные числа, сумма цифр которых равна 6.

3. Назовите все двузначные числа, разность цифр которых равна 7.

4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырехзначное число.

5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырехзначное число.

6. Выразите в сантиметрах:

1) 7 дм 4 см = 74 см
2) 4 м 1 см = 401 см
3) 2 м 6 дм = 260 см
4) 1 м 2 дм 5 см = 125 см

7. Выразите в дециметрах и сантиметрах:

1) 72 см = 7 дм 2 см
2) 146 см = 14 дм 6 см
3) 450 мм = 4 дм 5 см
4) 8 м 40 мм = 80 дм 4 см

УПРАЖНЕНИЯ

44. Запишите все отрезки, изображенные на рисунке 15.

a) AB, BC, AC, BK
б) OP, OR, OT, PR, PT, RT
в) AE, EC, CD, AC, ED, AD
г) MN, NE, ME, EP, PQ, EQ, MQ, NP

45. Запишите все отрезки, изображенные на рисунке 16.

а) AO, OC, AC, BO, OD, BD, AD
б) MK, KN, NP, MN, KP, MP, FK, KE, FE, EN, NS, ES

46. Отметьте в тетради точки A, B, C, D и соедините их попарно отрезками. Сколько отрезков образовлось? Сколько образовалось отрезков с концом в точке А?

47. Начертите отрезки MN и AC так, чтобы MN=6 см 3 мм, AC = 5 см 3 мм.

48. Начертите отрезки EF и BK так, что EF = 9 см 2 мм, BK = 7 см 6 мм.

49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрез­ка АС?

50. Начертите отрезок TP, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?

51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.

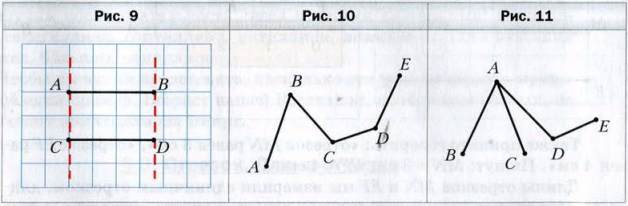
52. Назовите все ломаные, изобра­жённые на рисунке 11. Какая из них имеет наибольшее коли­чество звеньев?

53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

54. Запишите звенья ломаной, изображённой на рисунке 19, и измерь­те их длины (в миллиметрах). Вычислите длину ломаной.

55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клет­ки правее и на 1 клетку выше точки В; точку D — на 3 клетки пра­вее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точ­ки А, В, С, D и Е. Какая фигура образовалась? Запишите её назва­ние и укажите количество звеньев.

56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.

57. Вычислите длину ломаной MNKPEE, если MN = 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.

58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в мил­лиметрах) и найдите длину ло­маной.

59. Известно, что отрезок SK в 3 ра­за больше отрезка RS (рис. 21). Найдите длину отрезка RK, ес­ли RS = 34 см.

60. Известно, что отрезок DВ в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, ес­ли АD = 135 см.

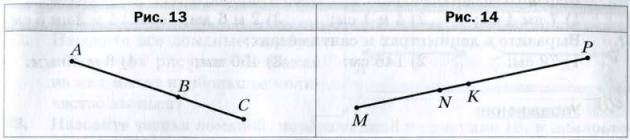
61. Известно, что AC = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.

62. Известно, что MF= 43 см, МЕ = 26 см, КЕ = 18 см (рис. 24). Найди­те длины отрезков МК и EF.

63. Даны две точки А и В. Сколько можно провести отрезков, соеди­няющих эти точки? Сколько можно провести ломаных, соединяю­щих эти точки?

64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому от­резку, причём точка К лежит между точками М и В, AM =12 см, ВК = 9 см. Найдите длину отрезка МК.

66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрез­ка ВС? Есть ли в условии задачи лишние данные?

67. Отрезки МТ и FK равны (рис. 25). Сравните отрезки MF и ТК.

68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ло­маной.

69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.

70. Вычислите длину ломаной, изображённой на рисунке 26.

71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.

72. Известно, что MF = 30 см, ME = 18 см, KF = 22 см (рис. 28). Найди­те длину отрезка КЕ.

73. Известно, что КР = РЕ = EF = FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.

74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?

75. Известно, что АЕ = 12 см, AQ = QB, ВМ = МС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.

76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них было две от­меченные точки, не считая концов отрезков?

77. У Миши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис. 32). Как, пользуясь этой линейкой, он может постро­ить отрезок длиной: 1) 3 см; 2) 2 см; 3) 1 см?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

78. Вычислите:

79. Выполните действия:

80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограм­мов больше подарили конфет, чем печенья?

81. Медведица Настасия Петровна заготовила на зиму семь бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасия Петровна?

82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть при­везённых фруктов продали в первый день, а остальные — во второй день. Сколько килограммов фруктов продали во второй день?

83. Кот Матроскин вырастил в своём саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского са­да, пятую часть всех фруктов — друзьям из школы, а остальное — в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?

84. Укажите наименьшее натуральное число, сумма цифр которого равна 101.

Источник

Отрезок. Длина отрезка

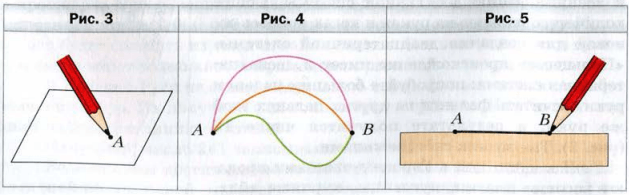
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3 ).

Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком.

Точка и отрезок − примеры геометрических фигур.

Точки A и B называют концами отрезка.

Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов : AB или BA. Читают: «отрезок AB» или «отрезок BA».

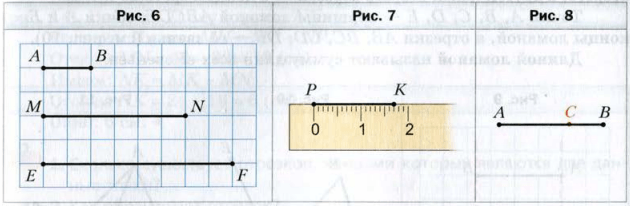
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.

Длины отрезков MN и EF мы измерили единичным отрезком, длина которого равна 1 см. Для измерения отрезков можно выбрать и другие единицы длины, например: 1 мм, 1 дм, 1 км. На рисунке 7 длина отрезка равна 17 мм. Он измерен единичным отрезком, длина которого равна 1 мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7 ).

Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается.

Длина отрезка обладает следующим свойством.

Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).

На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.

Два отрезка называют равными, если они совпадут при наложении.

Следовательно отрезки AB и CD равны. Пишут : AB = CD.

Равные отрезки имеют равные длины.

Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6 отрезок EF больше отрезка MN.

Длину отрезка AB называют расстоянием между точками A и B.

Длиной ломаной называют сумму длин всех ее звеньев.

На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми.

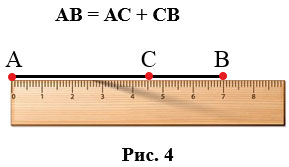
Решение. Имеем : BC = 8 − 3 = 5 (см).

Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC = 8 + 5 = 13 (см).

Источник