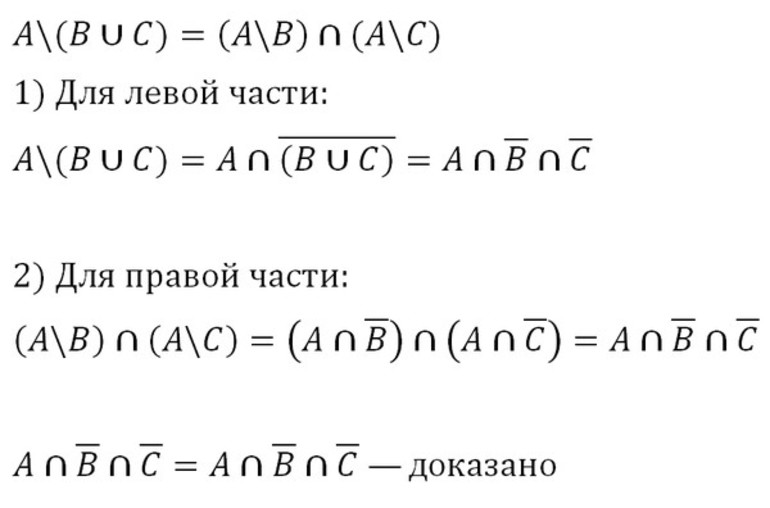Что означает доказать тождество

Тождество. Тождественные преобразования. Примеры.

Тождества в основном применяются для решения линейных уравнений.

Тождеством называется равенство, которое верно при всех значениях переменных.

Или другими словами, тождество — это равенство, которое выполняется на всём множестве значений переменных, входящих в него, например:

В этих выражениях при всех значениях a и b равенство верное.

2 выражения с равными значениями при всех значениях переменных являются тождественно равными.

Равенство x+2=5 может существовать не при всех значениях x, а лишь при x=3. Это равенство не будет тождеством, это будет уравнением. Кроме того, тождеством будет равенство, которое не содержит переменные, например 25 2 =625.

Тождественное равенство обозначают символом «≡» (тройное равенство).

Примеры тождеств.

— Тождество Эйлера (кватернионы);

— Тождество Эйлера (теория чисел);

— Тождество четырёх квадратов;

— Тождество восьми квадратов;

Тождественные преобразования.

Тождественное преобразование выражения (преобразование выражения) – это подмена одних выражений другими, тождественно равными друг другу.

Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.

Выполним тождественные преобразования с такой дробью: .

Полученное тождество, при х ≠ 0 и х ≠ 1 (недопустимые значения), т.к. знаменатель левой части не может быть равен нулю.

Доказательство тождеств.

Для того, чтоб доказать тождество нужно сделать тождественные преобразования обеих или одной части равенства, и получить слева и справа одинаковые алгебраические выражения.

Например, доказать тождество:

Вынесем х за скобки:

Это равенство есть тождество, при х≠0 и х≠1.

Чтоб доказать, что равенство не является тождеством, нужно найти 1-но значение переменной (которое допустимо) у которой числовые выражения (которые были получены) станут не равными друг другу.

5−1 ≠ 5+1 — подставим, к примеру, 5.

Это равенство не тождество.

Разница между тождеством и уравнением.

Тождество верно при всех значениях переменных, а уравнение – это равенство, которое верно только при одном либо нескольких значениях переменной.

Это выражение верно лишь при х = 10.

Тождеством будет равенство, которое не содержит переменных.

Источник

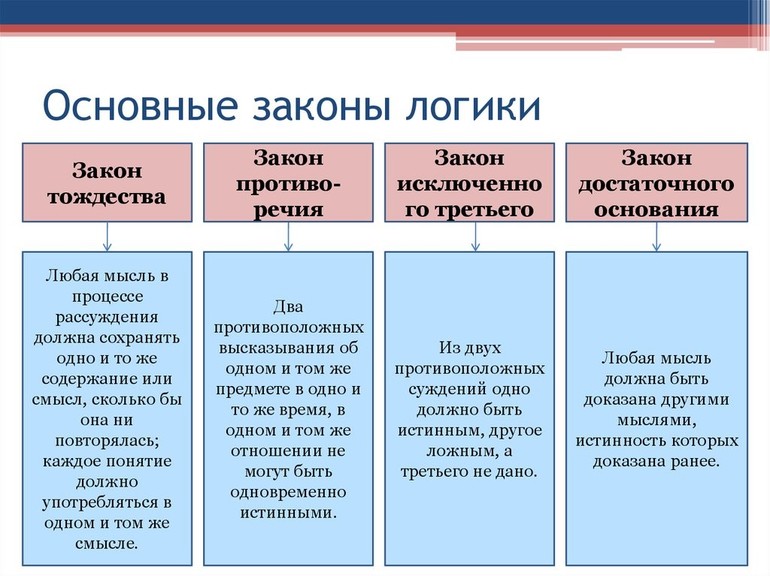
Основные законы логики

Логика — это раздел философии. Он представляет собой науку о формах и законах правильного мышления. Закон логики — необходимая связь между логическими формами в процессе построения последовательного рассуждения. Цель его состоит в формулировании правил и рекомендаций, с помощью которых можно найти путь к истине. Это не законы самого окружающего мира, а правила мышления о нём.

Аристотель, который создал классификацию свойств бытия, всесторонне определяющих субъект, впервые сформулировал три из четырёх логических законов и подразумевал под этим предпосылку для объективной связи мыслей в процессе размышления. Основными в формальной логике считаются законы:

Без этого закона невозможно установить, что такое логическое следование, и понять смысл доказательства.

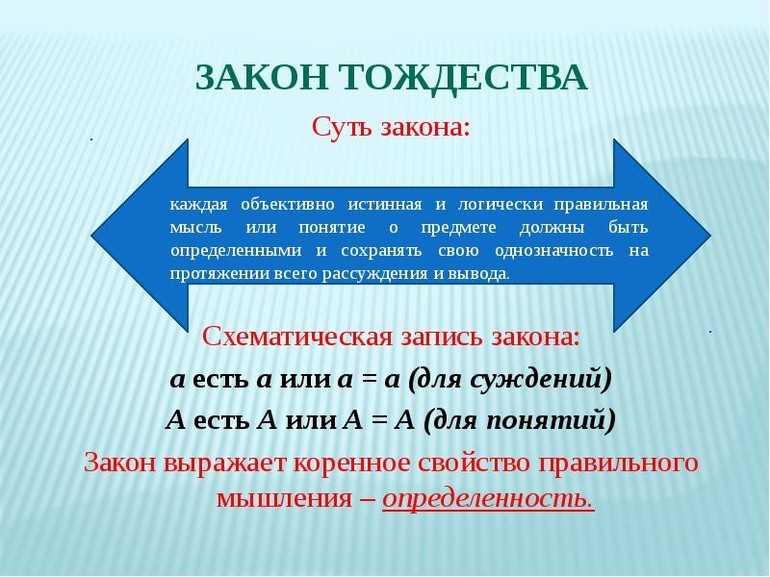
Логический принцип тождественности

Тождество — это примерное равенство, сходство объектов по какому-либо показателю. Принцип (синоним слова закон) его — один из основных логических законов формальной логики как науки, в соответствии с которым в процессе размышления любое суждение должно оставаться тождественными самому себе.

Аристотель формулировал это положение так: «Иметь не одно значение — значит, не иметь ни одного значения». В виде формулы этот принцип записывается следующим образом: А есть А или А = А, где А — мысль, которая может быть любой. На этом законе основаны многие положения логики. Например, следующие:

Нарушение закона тождества — пример, который привёл к логической ошибке. Ученик на уроке спрашивает учителя: «Можно наказывать человека за то, чего он не сделал?». «Конечно, нельзя», — отвечает учитель. «В таком случае не наказывайте меня, — говорит ученик, — я не сделал домашнюю работу». В этом диалоге нарушен логический принцип тождества, так как понятие «не сделал» применяется в разных значениях:

Получилось, что в одно и то же понятие было вложено два различных смысла. Нарушение закона может выражаться в следующих формах:

Нарушение закона тождества ведёт к неясности мысли, что совершенно недопустимо во многих областях, например, в юриспруденции. Неточное определение или неправильно истолкованное понятие в сфере права способствует появлению беззакония и произвола, поэтому в процессе мышления принцип тождественности выступает в виде важного правила.

Этот закон вводит требование об отсутствии в ходе размышлений подмены или смешения мысли об объекте или замены предмета мысли. Нужно учитывать, что даже в законодательных актах часто попадаются двусмысленности, а это обязательно приводит к разночтениям в истолковании и неоднозначности в применении.

Виды преобразований

Тождеством в математике называется равенство, которое верно при всех значениях, входящих в него переменных для различных классов функций. Значение этого слова — полное сходство, подобие объектов, явлений друг другу или самим себе. К тождествам можно отнести:

Тождество Эйлера — e iπ + 1 = 0 — часто приводят как пример феноменального результата, который устанавливает неочевидную зависимость между геометрией (число пи) и математическим анализом (экспонента). Формула связывает пять фундаментальных математических констант:

Тождественным преобразованием называются операции, которые проводятся для замены исходного выражения на тождественно равное. Например, x 3 — xy 2 = x (x — y)(x + y) — это тождество, так как вынесение за скобки общего множителя и применение формул сокращённого умножения являются тождественными преобразованиями. Для демонстрации подставим вместо переменных x и y произвольные значения. Пусть x = 5; y = 4. Получим слева: 125 — 5 x 16 = 45, справа 5 (5 — 4)(5 + 4) = 45. Совпадение обеих частей равенства доказывает тождественность.

Способы доказательства

Равенство и тождество, которое относится к предельному случаю равенства, — это термины, используемые в математике при решении уравнений. Для доказательства тождества нужно сделать тождественные преобразования выражений в одной или обеих частях равенства и получить одинаковые результаты. При выполнении преобразований необходимо обращать внимание на область допустимых значений (ОДЗ) переменных. Эти операции могут суживать ОДЗ или оставлять её прежней.

При переходе от выражения x + (-y) к выражению (x — y) область допустимых значений переменных x и y будет прежняя. Переход от выражения (x — 5) к отношению (x — 5) 2 / (x — 5) приводит к сужению ОДЗ переменной x от (-ꚙ, +ꚙ) до (-ꚙ, 5) U (5, +ꚙ). Способы доказательства:

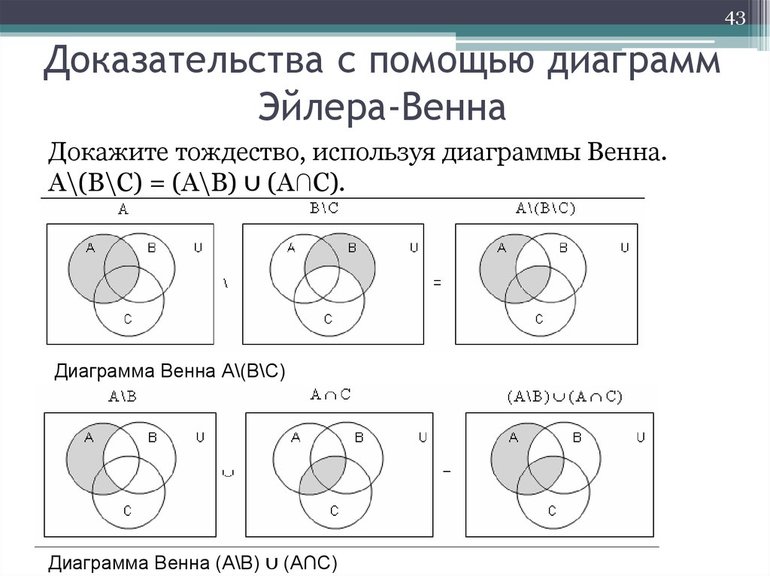
В теории множеств для доказательства тождественности часто используются круги или диаграммы Эйлера.

В них графическими методами наглядно можно представить различные операции над множествами: пересечение, объединение, разность, симметрическую разность. Существуют методы построения пересекающихся кругов Эйлера для любого выражения онлайн. Это тоже упрощает доказательство тождественности.

Чтобы доказать нетождественность двух частей выражения, требуется найти хотя бы одно значение переменной из области допустимых значений. При ее подстановке числовые выражения частей получатся неравными друг другу. Разница между уравнением и тождеством заключается в том, что первое может быть выполнено только при некоторых значениях переменных, которые будут его решением, а второе — при всех значениях.

Тождество — это многозначный термин, применяемый в философии, математике, физике. Понятие тождественности уникально по охвату им различной проблематики. С ним сталкиваются и школьники на уроках алгебры и геометрии, и крупные учёные при проведении многочисленных исследований в современной науке.

Источник

Лекция №3. Доказательство тождеств

ЛЕКЦИЯ №3 Доказательство тождеств

Цель: 1. Повторить определения тождества и тождественно равных выражений.

2.Ввести понятие тождественного преобразования выражений.

3. Умножение многочлена на многочлен.

4. Разложение многочлена на множители способом группировки.

Пусть каждый день и каждый час

Пусть добрым будет ум у нас,

А сердце умным будет!

В математике существует множество понятий. Одно из них тождество.

Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят. Некоторые тождества мы уже знаем.

Например, все формулы сокращенного умножения являются тождествами.

Формулы сокращенного умножения

4. a3 ± b3 = (a ± b)(a2 ab + b2).

Доказать тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части.

В алгебре существует несколько различных способов доказательства тождеств.

Способы доказательства тождеств

Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным. Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным. Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.

Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.

Как видите способов достаточно много. Какой способ выбрать в данном конкретном случае, зависит от тождества, которое вам необходимо доказать. По мере того, как вы будете доказывать различные тождества, придет и опыт в выборе способа доказательства.

Пример 1. Докажите тождество x·(a+b) + a·(b-x) = b·(a+x).

Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.

x·(a+b) + a·(b-x) = x·a +x·b + a·b – a·x.

Приведем подобные слагаемые и вынесем общий множитель за скобку.

x·a + x·b + a·b – a·x = x·b + a·b = b·(a + x).

Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.

В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.

(a+5)·(a+2) = (a²) + 5·a +2·a +10 = a²+7·a + 10.

Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.

« Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения»

Выяснить какое равенство является тождеством:

«Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений»

Умножение многочлена на многочлен

Умножим многочлен a + b на многочлен c + d. Составим произведение этих многочленов:
(a+b)(c+d).
Обозначим двучлен a + b буквой x и преобразуем полученное произведение по правилу умножения одночлена на многочлен:
(a+b)(c+d) = x(c+d) = xc + xd.
В выражение xc + xd. подставим вместо x многочлен a+b и снова воспользуемся правилом умножения одночлена на многочлен:
xc + xd = (a+b)c + (a+b)d = ac + bc + ad + bd.
Итак: (a+b)(c+d) = ac + bc + ad + bd.
Произведение многочленов a + b и c + d мы представили в виде многочлена ac + bc + ad + bd. Этот многочлен является суммой всех одночленов, получающихся при умножении каждого члена многочлена a + b на каждый член многочлена c + d.
Вывод: произведение любых двух многочленов можно представить в виде многочлена.
Правило: чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Заметим, что при умножении многочлена, содержащего m членов на многочлен, содержащий n членов в произведении до приведения подобных членов должно получиться mn членов. Этим можно воспользоваться для контроля.

Разложение многочлена на множители способом группировки:

1. Способы доказательства тождеств.

2. Что называют тождественным преобразованием выражения.

3. Умножение многочлена на многочлен.

4. Разложение многочлена на множители способом группировки

Источник

Как доказать тригонометрическое тождество?

Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.

А вот выражение \(\frac=x\) является тождеством только при условии \(x≠0\) (иначе левая часть не существует).

Как доказывать тождество?

Рецепт до одури прост:

Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».

Для того, чтоб это сделать можно:

Пример. Доказать тригонометрическое тождество \(\sin⁡2x=2\sin⁡x\cdot \cos\)
Решение:

\(\sin⁡2x=2 \sin⁡x\cdot \cos \)

Будем преобразовывать левую часть.
Представим \(2x\) как \(x+x\)…

Левая часть равна правой – тождество доказано.

Будем преобразовывать только левую часть. Приведем слагаемые к общему знаменателю.

Применим в числителе вездесущие основное тригонометрическое тождество: \(\sin^2⁡+\cos^2<⁡x>=1\).

Левая часть равна правой, тождество доказано.

Левая часть равна правой, тождество доказано.

Сократим дробь на \(\cos<⁡t>+\sin<⁡t>\).

Почленно разделим дробь, превратив ее в две отдельные дроби.

Левая часть равна правой, тождество доказано.

Как видите, все довольно несложно, но надо знать все формулы и свойства.

Как доказать основное тригонометрическое тождество

Два простых способа вывести формулу \(\sin^2x+\cos^2x=1\). Нужно знать только теорему Пифагора и определение синуса и косинуса.

Ответы на часто задаваемые вопросы:

Источник

Тождества: определение, обозначение, примеры

Начнем разговор о тождествах, дадим определение понятия, введем обозначения, рассмотрим примеры тождеств.

Что представляет собой тождество

Начнем с определения понятия тождества.

Тождество представляет собой равенство, которое верно при любых значениях переменных. Фактически, тождеством является любое числовое равенство.

По мере разбора темы мы можем уточнять и дополнять данное определение. Например, если вспомнить понятия допустимых значений переменных и ОДЗ, то определение тождества можно дать следующим образом.

Тождество – это верное числовое равенство, а также равенство, которое будет верным при всех допустимых значениях переменных, которые входят в его состав.

Про любые значения переменных при определении тождества речь идет в пособиях и учебниках по математике для 7 класса, так как школьная программа для семиклассников предполагает проведение действий исключительно с целыми выражениями (одно- и многочленами). Они имеют смысл при любых значениях переменных, которые входят в их состав.

Программа 8 класса расширяется за счет рассмотрения выражений, которые имеют смысл только для значений переменных из ОДЗ. В связи с этим и определение тождества меняется. Фактически, тождество становится частным случаем равенства, так как не каждое равенство является тождеством.

Знак тождества

Обычно запись тождества ничем не отличается от записи обыкновенного равенства. Знак тождества может быть применен для того, чтобы подчеркнуть, что перед нами не простое равенство, а тождество.

Примеры тождеств

Обратимся к примерам.

Равенства 2 + 3 = 5 и 7 − 1 = 2 · 3 также можно считать тождествами, так как они являются вернными. Здесь также допустима запись 2 + 3 ≡ 5 и 7 − 1 ≡ 2 · 3 .

Тождества могут содержать не только числа, но также и переменные.

Это значит, что приведенные равенства не являются тождествами.

В математике мы постоянно имеем дело с тождествами. Делая записи действий, производимых с числами, мы работаем с тождествами. Тождествами являются записи свойств степеней, свойств корней и прочие.

Источник