Что означает двоичное значение
Как читать двоичный (бинарный) код
Если вам интересно узнать, как читать двоичные числа, важно понять, как работают двоичные числа. Двоичная система известна как система нумерации «base 2», что означает наличие двух возможных чисел для каждой цифры; один или ноль. Большие числа записываются путем добавления дополнительных двоичных единиц или нулей.
Понимание двоичных чисел
Знание того, как читать двоичные файлы, не является критичным для использования компьютеров. Но хорошо понять концепцию, чтобы лучше понять, как компьютеры хранят числа в памяти. Он также позволяет понимать такие термины, как 16-битные, 32-битные, 64-битные и измерения памяти, такие как байты (8 бит).
Как читать двоичный код
«Чтение» двоичного кода обычно означает перевод двоичного числа в базовое 10 (десятичное) число, с которым люди знакомы. Это преобразование достаточно просто выполнить в своей голове, когда вы поймете, как работает бинарный язык.
Каждая цифра в двоичном числе имеет определенное значение, если цифра не является нулем. После того как вы определили все эти значения, вы просто складываете их вместе, чтобы получить 10-значное десятичное значение двоичного числа. Чтобы увидеть, как это работает, возьмите двоичное число 11001010.
2. Затем перейдите к следующей цифре. Если это один, то рассчитайте два в степени одного. Запишите это значение. В этом примере значение равно степени два, равной двум.
3. Продолжайте повторять этот процесс, пока не дойдете до самой левой цифры.
4. Чтобы закончить, все, что вам нужно сделать, это сложить все эти числа вместе, чтобы получить общее десятичное значение двоичного числа: 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202.
Двоичные числа с подписью
Приведенный выше метод работает для базовых двоичных чисел без знака. Однако компьютерам нужен способ представления отрицательных чисел также с помощью двоичного кода.
Из-за этого компьютеры используют двоичные числа со знаком. В системе этого типа самая левая цифра известна как знаковый бит, а остальные цифры известны как биты амплитуды.
Чтение двоичного числа со знаком почти такое же, как и без знака, с одним небольшим отличием.
1. Выполните ту же процедуру, как описано выше для двоичного числа без знака, но остановитесь, как только вы достигнете самого левого бита.
2. Чтобы определить знак, осмотрите крайний левый бит. Если это единица, то число отрицательное. Если это ноль, то число положительное.
4. Бинарный метод со знаком позволяет компьютерам представлять числа, которые являются положительными или отрицательными. Однако он потребляет начальный бит, а это означает, что для больших чисел требуется немного больше памяти, чем для двоичных чисел без знака.
Двоичные числа
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
Содержание
Таблица умножения двоичных чисел
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 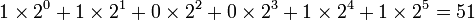
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
Полезное
Смотреть что такое «Двоичные числа» в других словарях:
Двоичные приставки — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
Прямой код (представление числа) — Прямой код способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел. Содержание 1 Представление числа в прямом коде 1.1 Примеры … Википедия
Шестнадцатеричные числа — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Шестнадцатиричные числа — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Комбинированная система счисления — В комбинированных системах счисления для записи чисел используются две или более систем счисления с разными основаниями. В общем случае возможно бесконечное множество комбинированных систем счисления. В спаренных (сдвоенных, двойных) системах… … Википедия
КОМПЬЮТЕР — устройство, выполняющее математические и логические операции над символами и другими формами информации и выдающее результаты в форме, воспринимаемой человеком или машиной. Первые компьютеры использовались главным образом для расчетов, т.е.… … Энциклопедия Кольера
Цифровой компаратор — или компаратор амплитуд является электронным устройством, берущим два числа в двоичном виде и определяющим, является ли первое число меньшим, большим или равным второму числу. Компараторы используются в центральных процессорах и микроконтроллерах … Википедия
Сумматор — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов.[1] Содержание 1 История 2 Классификация сумматоров … Википедия
Мнемоника — Содержание 1 Основной метод запоминания в современной мнемонике 2 История … Википедия
Что такое двоичная система счисления
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Видео
Мы привыкли шифровать десятью знаками
У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.
Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.
Например, перед нами число 19 547. Мы знаем, что в нём есть:
Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:
Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.
Двоичная система (тоже нормальная)
Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.
Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:
4 — 💡 ⚫⚫ 5 — 💡 ⚫ 💡 6 — 💡 💡 ⚫ 7 — 💡 💡 💡
Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:
256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332
Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.
Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 1 | 1 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Практика
Без практики объяснить, как этим пользоваться – трудно. Поэтому рассмотрим пару примеров. Однако для начала вам необходимо скачать таблицу, где значения бинарного кода представляются в десятичной форме. Я взял первую попавшуюся таблицу с интернета. Выглядеть она будет примерно так:
Задача 1: Представить 7 в двоичном коде, а потом расписать его с помощью формулы выше.
Для того чтобы это сделать надо:
Как видно из примера здесь нет ничего сложного. Давайте разберем что-нибудь посложнее, да и найдем таблицу посерьезнее. Я взял вот такую:
Задача 2: отобразить 13 в двоичной системе счисления.
Все шаги останутся точно такими же, однако я покажу другой способ для выполнения первого пункта. Принцип тот же, но он кажется мне более удобным.
Получаем что
Смотрим что в таблице:
Далее я приведу несколько свойств, которые вы сможете применить при работе с двоичной системой.
Как считать
Как использовать двоичную систему для записи чисел? Так же как и десятичную. Самым простым примером можно считать кодовый замок, такой как на чемоданах. Каждый диск которого, вращается и может принимать значение от 0 до 9. Достаточно представить, что вместо десяти цифр есть только 2, ноль и единица.
Так как система позиционная, это будет выглядит так:
Сейчас здесь записано число «ноль». Чтобы получилась единица, нужно провернуть крайний правый диск один раз.
Начинается самое интересное, как будет выглядеть число «два»? Крутим правое колесико… И снова получаем 0, ведь других значений нет. Нужно поступить так же, как и в десятичной системе, перенести разряд влево. Только в десятичной, это происходит когда значение превышает 9, а в двоичной сразу после 1.
| Двоичная система | Десятичная система |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Сто в двоичной системе — это 1100100.
Очень интересно в бинарной системе выглядит таблица умножения:
Легко запомнить, неправда ли? 0*0=0, 0*1=0, 1*1=1… И все!
Все математические операции выполняются точно так же
Если сложит в столбик то получается нагляднее
100
Складываем ноли, получаем 0, складываем две единицы, получаем ноль (2 раза провернули диск) и единичку переносим вправо.
Как видите, математика та же, вот только запись чисел неудобная, слишком много нолей и единиц, для человека — неудобно, машине же все равно.
Так же как с цифрами можно поступить с буквами. Латинская буква «a» будет выглядеть как 01001010 кириллическая «а» — 000011100010111000011001, и даже пробел — 00010100.
История создания
Ясно, что человечество пользовалось двоичным кодом очень давно. И сигнальные системы с дымом от костров и даже китайская Книга Перемен (700 лет до нашей эры) с ее гексаграммами известны очень давно. Но окончательно практический смысл бинарный код получил совсем недавно (если не считать азбуку Морзе).
Великий Лейбниц занимался двоичной системой в 17 веке, но применить бинарную систему счисления было особо негде. В том же Веке Паскаль создал свою счетную машину (суммирующую), использующую десятичную систему. Оказалось, что считать на таком «калькуляторе» не так уж и удобно.
Суммирующая машина Паскаля (десятичная)
И только в 40-х годах 20 веке, вместе с появлением первых электронный вычислительных машин двоичный код явил всю свою безусловную полезность и красоту. Именно как машинный язык. Записывать информацию в котором гораздо проще, чем привычными нам средствами, буквами и цифрами.
То же самое, в двоичном коде можно сделать проще
Для чего нужна двоичная система счисления сегодня, мы прекрасно знаем, у каждого в кармане есть смартфон. На самом деле, ноли и единицы используются намного чаще, чем десятичная система, даже если мы, люди, этого и не видим. Не удивительно, мы использовали двоичную систему на протяжении всей истории, но до эры машин даже не замечали этого.
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Большое спасибо! Очень хорошо объяснили. Всё понял.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
поделитесь, пожалуйста, еще постами по информатике если есть
А теперь слушайте домашнее задание: построить синхрофазотрон.
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
На самом деле все еще проще.
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
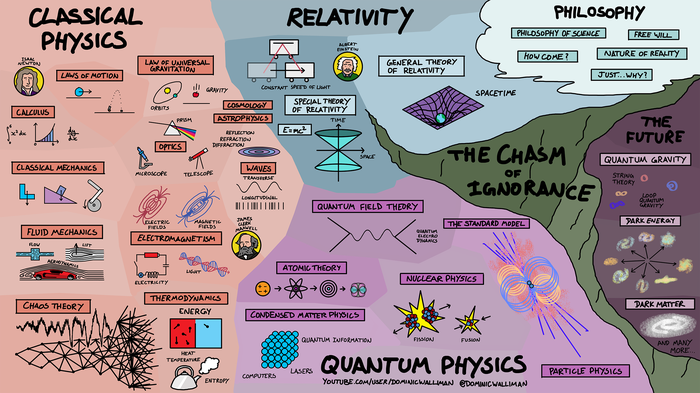
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.