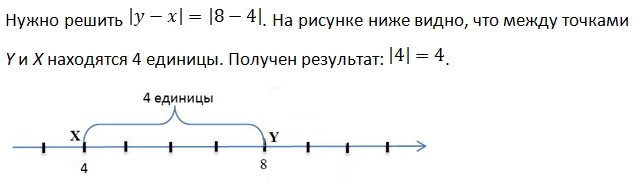
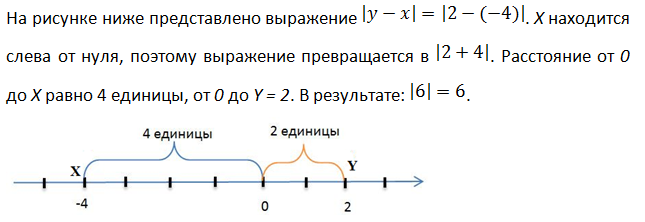
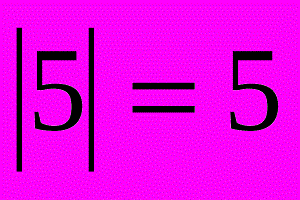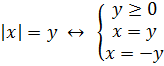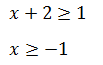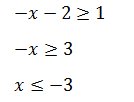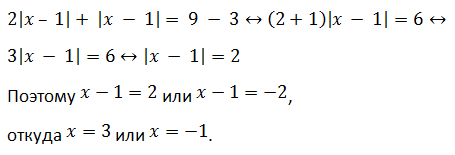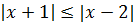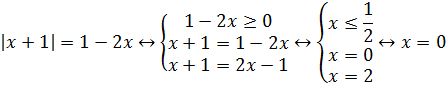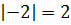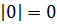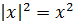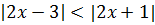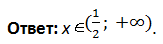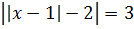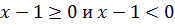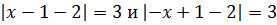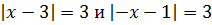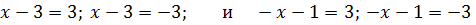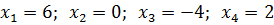Что означает двойной модуль
Математическая энциклопедия
— 1) То же, что бимодуль.2) Пара подгрупп Ни Fгруппы G, участвующая в разложении группы Gна двойные смежные классы, т. е. в разбиении G на непересекающиеся подмножеетва вида HxF, где х- элемент из G. Подмножество HxF наз. смежным классом группы Gпо Д. м. ( Н, F), или двойным смежным классом группы G ло модулю ( Н, F). Напр., разложение группы порядка 24 на двойные смежные классы по модулю ( Н, F), где Ни F- ее силовские 2- и 3-подгруппы, состоит из одного смежного класса по Д. м. ( Н, F). Любой двойной смежный класс HxF состоит из смежных классов группы Gпо подгруппе Fи одновременно из смежных классов группы Gпо подгруппе Н, где |U:V| означает индекс подгруппы Vв группе U. Лит.:[1] Холл М., Теория групп, пер. с англ., М., 1962. В. Д. Мазуров.
Смотреть значение Двойной Модуль в других словарях
Двойной — удвоенный, сдвоенный, взятый или сделанный вдвое, вдвойне, дважды; передвоенный, сугубый, вдвое больший. труд, двойная и плата. Зубы двойные, а руки одинакие, о еде и работе.
Толковый словарь Даля
Двойной — двойная, двойное. 1. Вдвое больший, увеличенный в два раза. расход. Материя двойной ширины. Двойное жалование. 2. Состоящий из двух однородных частей, предметов. подбородок.
Толковый словарь Ушакова
Двойной Прил. — 1. Состоящий из двух одинаковых или подобных предметов, элементов, частей и т.п. // Осуществляемый в два приема, повторяющийся дважды. 2. Проявляющийся в двух видах; двоякий.
Толковый словарь Ефремовой
Аукцион Двойной — форма проведения торга, в котором конкурируют и продавцы, и покупатели, а цена устанавливается на уровне равновесия спроса и предложения, когда число продавцов по этой.
Экономический словарь
Аукцион Двойной — форма проведения
торга, в котором конкурируют и продавцы, и покупатели, а
цена устанавливается на уровне равновесия
спроса и
предложения, когда число.
Экономический словарь
Двойной Аукцион (double Auction) — – форма аукциона, в котором цены предлагают как покупатели, так и продавцы ценной бумаги. Проводится, если установленная биржевым «специалистом» разница цен покупки.
Экономический словарь
Двойной Валютный Курс — См. Курс валютный двойной
Экономический словарь
Двойной Выход — (Double Exit)
Использование двух паспортов для введения в
заблуждение или удобства.
Экономический словарь
Двойной Курс — метод государственного регулирования валютных операций, заключающийся в двойной котировке
курса национальной валюты: установлении разных курсов по финансовым.
Экономический словарь
Двойной Опцион — право
опциона либо купить, либо продать
контракт по базисной цене (но не купить и продать одновременно).
Экономический словарь
Двойной Орел — DOUBLE EAGLEЗолотая
монета США в 20 дол. весом 516 г и пробой 0,900.
Закон о
золотом
резерве, принятый 30 января 1934 г., приостановил чеканку ЗОЛОТЫХ МОНЕТ, и только.
Экономический словарь
Двойной Рейтинг — Ситуация, когда два основных рейтинговых агентства, таких, как Standard & Poors и Инвесторская служба Moodys, присваивают одним и тем же ценным бумагам различные рейтинги.
Экономический словарь
Двойной Таможенный Тариф — тариф, включающий два ряда ставок таможенных пошлин: минимальные для товаров стран, с которыми заключены специальные таможенные соглашения, и максимальные ставки для.
Экономический словарь
Двуствольный, Облигация С Двойной Гарантией — Муниципальная доходная облигация, основная сумма и проценты по которой гарантируются более крупным муниципальным ведомством. Например, орган, занимающийся эксплуатацией.
Экономический словарь
Контроль Двойной — англ. dual control действия требующие для их совершения одновременного согласия двух сторон, например, две подписи на документе, два ключа от банковского сейфа, арендуемого.
Экономический словарь
Курс Валютный Двойной — двойная котировка курса национальной валюты для коммерческих и финансовых операций.
Экономический словарь
Максимум Двойной — график изменения курса определенной ценной бумаги, согласно которому курс дважды поднимается до максимального уровня, что вызывает сопротивление повышению курса.
Экономический словарь
Минимум Двойной — график изменения курса ценных бумаг, согласно которому курс дважды опускается до своего минимального уровня и вновь поднимается. При анализе состояния рынка М.д. означает.
Экономический словарь
Опцион Двойной — CALL OF MOREТермин Лондонской фондовой
биржи, обозначающий
опцион, к-рый дает покупателю
право однократной покупки такого же количества акций по той же цене.
Экономический словарь
Орел Двойной — золотая монета в США достоинством в 20 долларов. Выпускается в тезаврационных целях.
Экономический словарь
ДВОЙНОЙ МОДУЛЬ
— 1) То же, что бимодуль.2) Пара подгрупп Ни Fгруппы G, участвующая в разложении группы Gна двойные смежные классы, т. е. в разбиении G на непересекающиеся подмножеетва вида HxF, где х- элемент из G. Подмножество HxF наз. смежным классом группы Gпо Д. м. ( Н, F), или двойным смежным классом группы G ло модулю ( Н, F). Напр., разложение группы порядка 24 на двойные смежные классы по модулю ( Н, F), где Ни F- ее силовские 2- и 3-подгруппы, состоит из одного смежного класса по Д. м. ( Н, F). Любой двойной смежный класс HxF состоит из 

Лит.:[1] Холл М., Теория групп, пер. с англ., М., 1962.
Смотреть что такое «ДВОЙНОЙ МОДУЛЬ» в других словарях:
Двойной интеграл — В математическом анализе кратным или многократным интегралом называют множество интегралов взятых от переменных. Например: Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число. Содержание 1… … Википедия
Число двойной точности — (Double precision, Double) компьютерный формат представления чисел, занимающий в памяти две последовательных ячейки (компьютерных слова; в случае 32 битного компьютера 64 бита или 8 байт). Как правило, обозначает формат числа с плавающей запятой… … Википедия
Мобильный модуль на шине PCI Express — (от англ. Mobile PCI Express Module (MXM)) стандарт взаимодействия для графических процессоров (Графические модули стандарта MXM) в лэптопах, в которых используется шина PCI Express, разработанная компанией Nvidia и несколькими производителями… … Википедия
БИМОДУЛЬ — двойной модуль, абелева группа В, являющаяся левым модулем над кольцом R и правым модулем над кольцом S, причем для любых В этом случае говорят, что имеет место ситуация или что Вявляется (R, S ) бимодулем. Б. Вможно рассматривать как левый… … Математическая энциклопедия
Спейсхэб — (англ. SPACEHAB) модуль, разработанный специально для полётов в американских многоразовых космических кораблях Спейс шаттл, который использовался в качестве грузового модуля или экспериментальной лаборатории в космосе на орбите Земли в … Википедия
Spacehab — Спейсхэб (англ. SPACEHAB) модуль, разработанный специально для кораблей спейс шаттл, который используется в качестве грузового модуля или экспериментальной лаборатории в космосе. Модуль «Спейсхэб» разработан в середине 80 х годов компанией с… … Википедия
STS-91 — Эмблема Полётные данные корабля … Википедия
Гори, Доминик Ли Падвилл — Доминик Ли Падвилл Гори Dominic Lee Pudwill Gorie Страна … Википедия
Дискавери STS-91 — п· Полётные данные корабля Название корабля Дискавери Стартовая площадка КЦ Кеннеди, СП 39 А[1] … Википедия
SGI Octane — SGI Octane2 (2000 2004) … Википедия
Модуль числа знак, свойства, действия, как найти, примеры графиков
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
Модуль комплексного числа
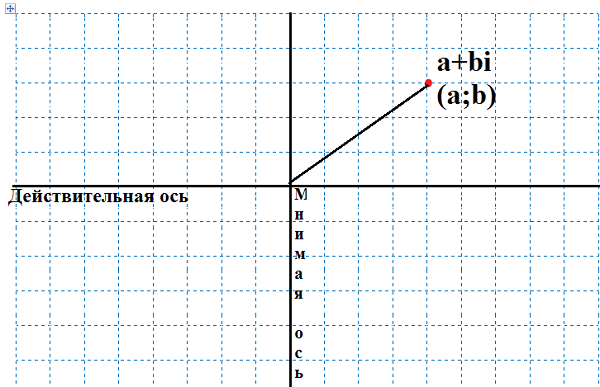
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x| <, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Далее простая арифметика − нужно решить два равенства относительно x.
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.
Ответ: 2 и −2.
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.
Это означает, что –2 – поворотная точка.
Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.
Разделим интервал на 2 части:
Общим ответом для этих двух неравенств является интервал [−1, + ∞).
Общим ответом для этих двух неравенств является интервал (−∞, –3].
Окончательное решение – объединение ответов отдельных частей:
Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).
Уравнения вида |x| = |y|
Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ: x1 = 3, x2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:
Решение:
Ответ: x = 0.
Модуль суммы
Модуль разности
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
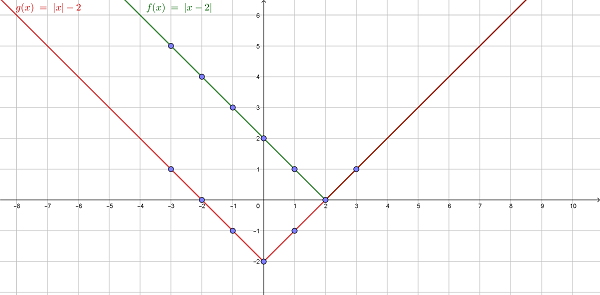
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение: из рисунка видно, что график симметричен относительно оси Y.
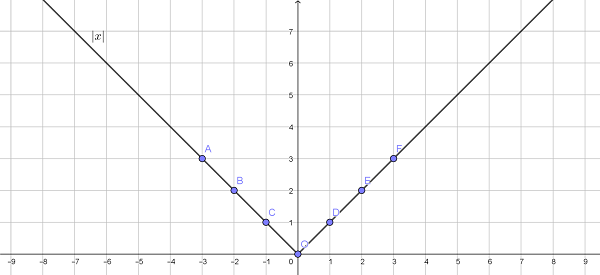
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
Пример 1. Решить методом интервалов.
Решение:
Результатом будет сумма всех подходящих интервалов.
Модуль в модуле
Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.
Лучше всего понять принцип на примере.
Пример 1. Решить
Решение:
Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:
В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:
Нужно упростить два уравнения:
Далее каждое из равенств разделяется еще на два:
Получено четыре результата:
Заключение
Самое важное, что нужно знать: модуль не может быть отрицательным.
Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.
В качестве итогов, напомним все свойства, которые помогут в решении задач:
Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.
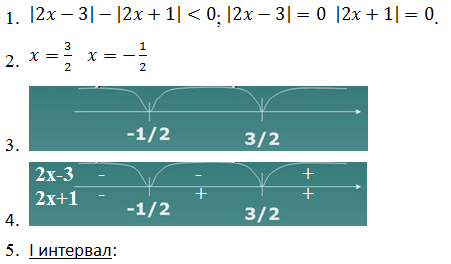
Неравенство с двумя модулями. Часть II
«Неравенство с двумя модулями. Часть I» смотрим здесь.
Решим неравенство
Правило раскрытия модуля говорит, что раскрытие модуля зависит от того, какой знак имеет подмодульное выражение. Стало быть, нас будут интересовать нули подмодульных выражений, – смена знака подмодульного выражения возможна только в них.
Вся числовая ось указанными точками разбивается на 4 промежутка. Нам предстоит поработать с неравенством в каждом из них.
Выясним, как распределяются знаки подмодульных выражений на каждом из промежутков.
Мы замечаем, что на двух промежутках (первом и третьем слева) знаки подмодульных выражений распределены одинаково.
Итак, первый случай:
Предстоит решить систему (мы объединили первый и третий промежутки в совокупность):
Во второй строке системы приводим подобные слагаемые и раскладываем на множители:
Теперь переходим на ось, пересекаем два множества между собой:
.
Второй случай:
.
Третий случай:
.
Нам осталось объединить решения каждого из случаев между собой:
Ответ:
Для тренировки предлагаю Вам решить следующее неравенство:
Двойной модуль как решать
Администратор
Роман
Tel. +380685083397
yukhym.roman@gmail.com
skype, facebook:
roman.yukhym

Решение задач
Андрей
facebook:
dniprovets25
Как решить простейшее модульное уравнение или уравнение содержащее модуль?
Обычно решение сводится к системе :

Сразу рассмотрим на примере решение уравнений.
Решите уравнение | x – 6| = 18.
Выражение стоящее под модулем приравниваем к 0:
Отмечаем 6 на координатной прямой, далее проверяем знак на каждом из получившихся интервалах.
На интервале (-∞; 6) возьмем число 0 и подставим
0-6=-6 получилось отрицательное число, значит на этом интервале будет знак “ – ”
На интервале (6;+∞) возьмем число 7 и подставим
7-6=1 получилось положительное число, значит на этом интервале будет знак “ + ”

Теперь решаем уравнения на каждом интервале.
(-∞; 6) здесь получился знак “ – ”, значит выражение под модулем поменяет знаки на противоположные:
(6;+∞) здесь получился знак “ + ”, значит выражение под модулем остается без изменения:
Видно, что 24 лежит на интервале (6;+∞) следовательно, является корнем уравнения.
Выражения стоящие под модулем приравниваем к 0:
2x – 5 = 0 и 4 — x = 0
x=2,5 и x=4
Отмечаем x=2,5 и x=4 на координатной прямой, далее проверяем знак на каждом из получившихся интервалах.
На интервале (-∞; 2,5) возьмем число 0 и подставим в каждое выражение
2*0-5=-5 получилось отрицательное число, значит на этом интервале будет знак “ – ”
4-0=4 получилось положительное число, значит на этом интервале будет знак “ + ”
На интервале (2,5; 4) возьмем число 3 и подставим в каждое выражение
2*3-5=1 получилось положительное число, значит на этом интервале будет знак “ + ”
4-3=1 получилось положительное число, значит на этом интервале будет знак “ + ”
На интервале (4; +∞) возьмем число 5 и подставим в каждое выражение
2*5-5=5 получилось положительное число, значит на этом интервале будет знак “ + ”
4-5=-1 получилось отрицательное число, значит на этом интервале будет знак “ – ”
Теперь решаем уравнения на каждом интервале.
(-∞; 2,5) здесь получился знак “ – ” у выражения “ 2x – 5 ”, значит выражение под модулем поменяет знаки на противоположные и знак “ + ” у выражения “ 4 — x ”, значит выражение под модулем остается без изменения:
(2,5; 4) здесь получился знак “ + ” у обоих выражений, значит выражения под модулем останутся без изменений:
(4; +∞) здесь получился знак “ – ” у выражения “ 4 — x ”, значит выражение под модулем поменяет знаки на противоположные и знак “ + ” у выражения “ 2x – 5 ”, значит выражение под модулем остается без изменения:
Решите уравнение ||x|-3|=15.
Так как в правой части стоит простое число то распишем на два уравнения (раскроем внешний модуль):
|x|=18
|x|=-12 (модуль не может равняться отрицательному числу, следовательно это уравнение не имеет решений)
Раскрываем модуль |x|=18
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Надеюсь, ты уже усвоил тему «Модуль числа» и таким образом уже частично готов к ЕГЭ по математике? 🙂
Если нет, срочно повтори эту тему. А если да, читай дальше.
Решение уравнений с модулем может быть самостоятельной задачей, но часто такие уравнения могут возникнуть при решении уравнений другого типа, например, квадратных.
Вот пример подобной ситуации:
Видно, что в правой части – квадрат числа :
Казалось бы, теперь достаточно просто убрать квадраты слева и справа, и получим линейное уравнение.
В таких ситуациях нужно быть предельно осторожным: ведь ты же помнишь простое правило:
Вот и появляется на сцене наш модуль:
Чтобы не теряться в таких случаях, давай разберемся, что из себя представляет решение уравнений с модулем.
Let’s dive right in. (Поехали!)
Решение уравнений с модулем вида |Х| = a
Давай разбираться на примерах. Необходимо решить уравнение вида:
То есть можно формализовано записать так:
А если вот такое уравнение:
Эти рассуждения можно было и обойти, вспомнив основное свойство модуля:
Модуль всегда положителен либо равен нулю!
Если обобщить разобранные выше примеры, то можно написать общее правило для решения уравнений вида :
Попробуем применить это правило для такого уравнения:
Выражение под знаком модуля изменилось, но на логике рассуждений это не отражается, поэтому давай решать уравнение, применяя наше правило:
А если уравнение имеет вид:
Что-то меняется в рассуждениях? Конечно, нет! Ну, тогда давай решать его!
Уловил? Закрепим на примерах.
Примеры для самостоятельной работы
Решения примеров для самостоятельной работы
Точно так же как и в предыдущем примере уравнения с модулем могут возникнуть при решении уравнений другого типа, например, иррациональных.
Вот пример подобной ситуации:
Мы могли бы раскрыть скобки, перенести все в одну сторону, привести подобные и решить обычное квадратное уравнение (например, через дискриминант).
Но здесь удобнее поступить по-другому!
Заметим, что в правой части уравнения – формула сокращённого умножения квадрат суммы:
Тогда уравнение станет таким:
Казалось бы, теперь достаточно просто убрать квадраты слева и справа, и получим линейное уравнение.
И опять на сцене наш модуль:
Чтобы не теряться в таких случаях, научимся решать уравнения с модулем (все три типа).
Три типа уравнений с модулем
1. Уравнения вида |X| = |a|
Большинство уравнений с модулем можно решить, используя одно только определение модуля. Например:
Решите уравнение:
Ответ:
Другой пример:
И правда, вспомним свойство №1:
, то есть модуль всегда неотрицателен.
Итак, мы выработали общее правило решения простейших уравнений с модулем:
Ещё примеры (как обычно, пробуй решить их сам, потом смотри решения):
Решения:
2. Уравнения вида |X| = |Y|
Если начнём раскрывать модули по определению, натолкнёмся на множество проверок: какое число больше нуля, какое меньше; в итоге получим большую совокупность, которая затем упростится.
Но можно сделать так, чтобы сразу было всё кратко.
Для этого вспомним свойство модуля №7:
С помощью этого свойства можем избавляться от модулей:
Пример:
Решение:
Реши самостоятельно:
Ответы:
3. Уравнения вида |X| = Y
Отличие от первого типа уравнений в том, что в правой части тоже переменная. А она может быть как положительной, так и отрицательной.
Поэтому в её неотрицательности нужно специально убедиться, ведь модуль не может равняться отрицательному числу (свойство №1):
Пример:
Решение:
Теперь задачи для самостоятельного решения:
Ответы:
Итак, исходное уравнение равносильно системе
Ответ:
Метод интервалов в задачах с модулем
Пример:
Решение:
Аналогично и со вторым:
Проблема только в том, что теперь нам нужно рассмотреть очень много вариантов: по варианта для каждого модуля, итого четыре разных, но похожих друг на друга, уравнения.
Если модулей будет не два, а три, получится уже уравнений!
Можно ли как-то сократить количество вариантов?
Да, можно – ведь не все условия могут выполняться одновременно: и противоречат друг другу.
Поэтому нет смысла раскрывать второй модуль «с плюсом», если первый раскрыт «с минусом». Значит, здесь у нас на одно уравнение меньше.
Теперь систематизируем то, что мы только что выяснили, и разработаем последовательность действий в таких примерах:
2. Отметим корни выражений под модулями на числовой оси:
3. Подпишем у каждого из получившихся интервалов, какой знак принимает каждое из наших подмодульных выражений.
4. Для каждого интервала запишем и решим уравнение. Важно проследить, чтобы ответы соответствовали интервалу!
-3″> – этот корень сторонний.
– этот корень попадает в «свой» интервал, значит, он подходит.
– этот корень тоже является решением.
Проверим полученные корни:
I. (корень и правда сторонний).
Ответ:
Примеры:
Решения:
Модуль в модуле
В некоторых уравнениях встречается «вложенный» модуль, то есть модуль какого-то выражения является частью подмодульного выражения, например:
Что делать в таком случае? Все банально: раскрывать модули. Но раскрывать их нужно по очереди. Какой будем раскрывать первым?
А это зависит от того, каким методом ты хочешь решить это уравнение. Рассмотрим два возможных варианта:
I. Данное уравнение является уравнением вида
В этом случае первый способ решения будет стандартным для такого типа:
Получили два элементарных уравнения такого же типа, то есть:
Эти четыре числа и будут ответом, можешь проверить их подстановкой в исходное уравнение.
II. Есть ещё один, более универсальный способ, который подойдёт для любых задач, не попадающих ни в какой из стандартных типов.
Метод интервалов.
В этом случае нужно раскрывать модули начиная с самых «глубоких», то есть «внутренних». В нашем случае внутренним будет модуль, выделенный красным цветом:
Краткое изложение статьи и основные формулы
Уравнения с модулем делятся на три вида, каждый вид имеет свой подход к решению:
Теперь тебе слово.
Как тебе. про уравнения с модулем? Легкотня! )
Напиши внизу в комментариях помогла тебе наша статья или нет.
Расскажи о своем опыте решения уравнений с модулем, если он у тебя был.
Возможно у тебя есть вопросы. Или предложения.
Напиши в комментариях. Мы читаем все.
И удачи на экзаменах!
P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это – не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время.
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте – нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь) и решебник и программу подготовки «100gia».
Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!
И в заключение.
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Комментарии
Спасибо огромное,повторил,сдал на отлично,Алексею нобелевскую по математике)
Марк, наши поздравления с отличной сдачей. Премию Алексею передам 🙂
Наградим поощрительной грамотой )
Добрый день! В пункте №3 Уравнения вида ∣x∣=y во втором примере: −2∣x+4∣=3−x, откуда дальше в решении появляется коэффициент 4 в правой части? −2∣x+4∣=3−4x Спасибо за ответ и Ваш чудесный и полезный сайт!
Роман, привет! Спасибо за замечания и слова благодарности. Очень ценно. Алексей Шевчук проверит и поправит, если там ошибка. Еще раз спасибо!
Роман, спасибо. Это была опечатка в условии.
А как решить такой пример 7|2-4|+4*-8
помогите,пожалуйста,решить уравнение дробь в модуле :числитель 13,296 знаменатель 3.71 минус модуль 0,4х минус4,7 модуль закрывается,далее от дроби минус 2,2 умножить на 1,4.Еще раз обращаю внимание: сама дробь в модуле И равно 8 Пожалуйста помогите
Здравствуйте, помогите пожалуйста решить такое уравнение |x-1|=2x+3
Gern geschehen, Dascha! Bitte. International Mathematical Unterstützung zu Ihren Diensten ))
Очень хорошо разобрано и объяснено. И за советы спасибо)
Лера, жму руку! Спасибо за теплые слова. Удачи на всех экзаменах!
Решите уравнение ∣x∣=−3. разве может модуль равняться отрицательному числу
Джозеф, нет, не может, и в этом примере поясняется, почему.
Помогите решить |х|+|y-x|=2 Нужно расскрыть модуль и по получившимся ответам которых 4 как сказал препод