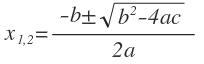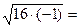Что означает если дискриминант меньше нуля

Дискриминант

Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.

Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt\) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед \(\sqrt\)

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Источник

Дискриминант
квадратного уравнения

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай
D > 0
(дискриминант больше нуля)

x_1;2 =

−b ± √ D

2a

x_1;2 =

−5 ± √ 81

2 · 2

x_1;2 =

−5 ± 9

4

x1 = −5 + 9 4	x2 = −5 − 9 4
x1 = 4 4	x2 = −14 4
x1 = 1	x2 = −3 2 4
x1 = 1	x2 = −3 1 2

Ответ: x₁ = 1; x₂ = −3

1

2

II случай
D = 0
(дискриминант равен нулю)

D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0

x_1;2 =

−b ± √ D

2a

x_1;2 =

− (−8) ± √ 0

32

x_1;2 =

8 ± 0

32

x =

8

32

x =

1

4

Ответ: x =

1

4

III случай
D
(дискриминант меньше нуля)

D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D

x_1;2 =

−b ± √ D

2a

x_1;2 =

− (−6) ± √ −36

32

Ответ: нет действительных корней

Источник

Все формулы связанные с дискриминантом

Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 – 4ac
ax 2 + 2kx + c = 0		k 2 – ac
x 2 + px + q = 0
		p 2 – 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 – 4ac
ax 2 + 2kx + c = 0	, где D = k 2 – ac
x 2 + px + q = 0	, где D =
	, где D = p 2 – 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-6) 2 – 4 · 1 · 9 = 36 – 36 = 0, D = 0

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 1 · (-5) = 16 + 20 = 36, D > 0

Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.

Квадратным уравнением называется уравнение вида

,

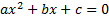
a,b,c – постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:

Формула дискриминанта: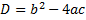

.

О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай
D > 0
(дискриминант больше нуля)

x1 =

−5 + 9

4

x₂ =

−144x₁ = 1x₂ = −3

24x₁ = 1x₂ = −3

II случай
D = 0
(дискриминант равен нулю)

D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0

III случай
D
(дискриминант меньше нуля)

D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D

Ответ: нет действительных корней

Источник

Как найти дискриминант квадратного уравнения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие квадратного уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.

Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.

Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Чаще всего для поиска дискриминанта используют формулу:

В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:

Эта формула подходит даже для неполных квадратных уравнений.

Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.

Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Примеры решения квадратных уравнений с помощью дискриминанта

Ответ: корень уравнения 3.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Источник

Что делать если дискриминант меньше нуля

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай
D > 0
(дискриминант больше нуля)

x1 =

−5 + 9

4

x₂ =−5 − 94x₁ =44x₂ =−144x₁ = 1x₂ = −324x₁ = 1x₂ = −312

II случай
D = 0
(дискриминант равен нулю)

D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0

III случай
D
(дискриминант меньше нуля)

D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D

Ответ: нет действительных корней

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример 42.4. Решить уравнение: .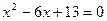

.

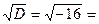
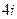
Тогда .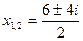

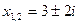
Ответ:

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Дата добавления: 2014-12-27 ; Просмотров: 12919 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 – 4ac
ax 2 + 2kx + c = 0		k 2 – ac
x 2 + px + q = 0
		p 2 – 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 – 4ac
ax 2 + 2kx + c = 0	, где D = k 2 – ac
x 2 + px + q = 0	, где D =
	, где D = p 2 – 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-6) 2 – 4 · 1 · 9 = 36 – 36 = 0, D = 0

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 1 · (-5) = 16 + 20 = 36, D > 0

Источник