Что означает изометрия в черчении

Изометрическая проекция

Изометри́ческая прое́кция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.

Содержание

Стандартные изометрические проекции [1]

Прямоугольная (ортогональная) изометрическая проекция

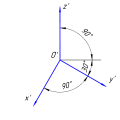
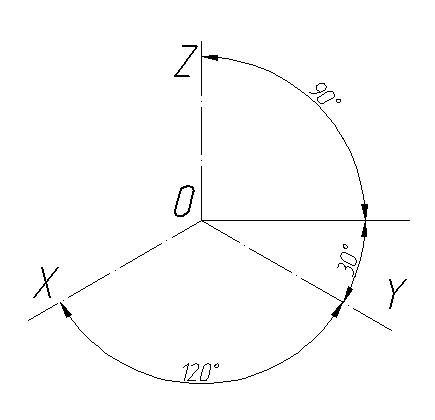
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения () имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.

Косоугольная фронтальная изометрическая проекция

Ось Z’ направлена вертикально, угол между осью X’ и Z’ равен 90°, ось Y’ с углом наклона 135° (допускается 120° и 150°) от оси Z’.

Фронтальная изометрическая проекция выполняется по осям X’, Y’ и Z’ без искажения.

Кривые параллельные фронтальной плоскости проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция

Ось Z’ направлена вертикально, между осью Z’ и осью Y’ угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X’ и Y’ равным 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям X’, Y’ и Z’.

Кривые, параллельные горизонтальной плоскости [2] проецируются без искажений.

Визуализация

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35.264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.

Матричные преобразования

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки в трёхмерном пространстве в точку на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35.264° и вокруг вертикальной оси (здесь y) на β = 45°:

Затем применяется ортогональная проекция на плоскость x-y:

Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда. [3]

Ограничения аксонометрической проекции

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку наши глаза или фотография работают иначе.

Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.

Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.

Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.

Изометрическая проекция в компьютерных играх и пиксельной графике

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика (англ.) могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования визуальной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctan 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

История изометрических компьютерных игр

На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу. [18]

Источник

Аксонометрические проекции

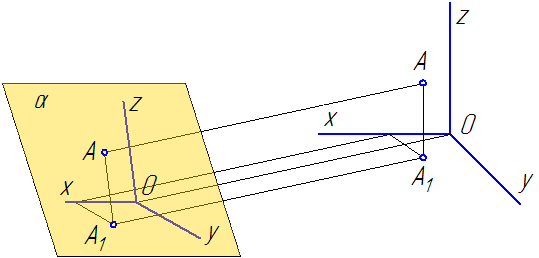
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2
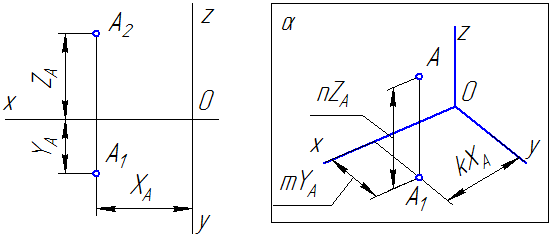
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

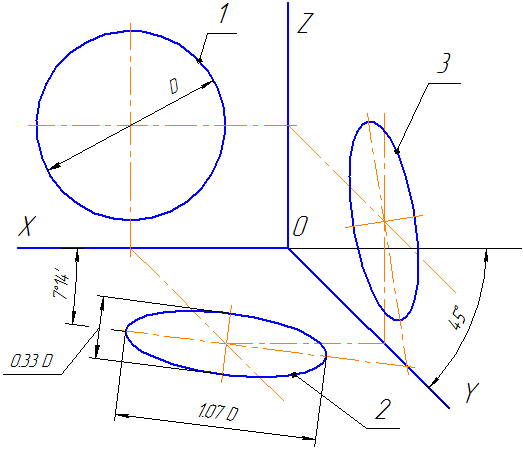
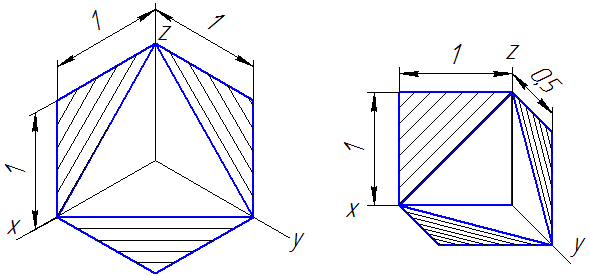
4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

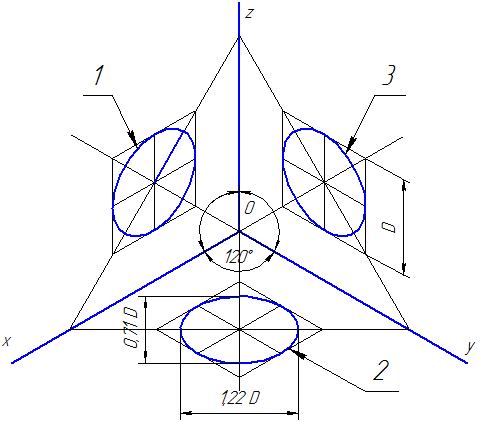
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

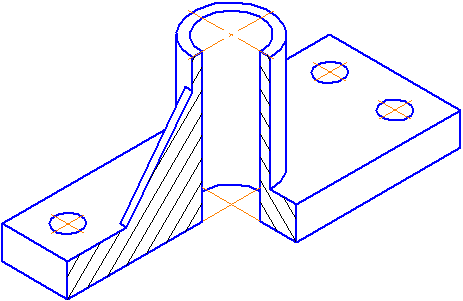
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

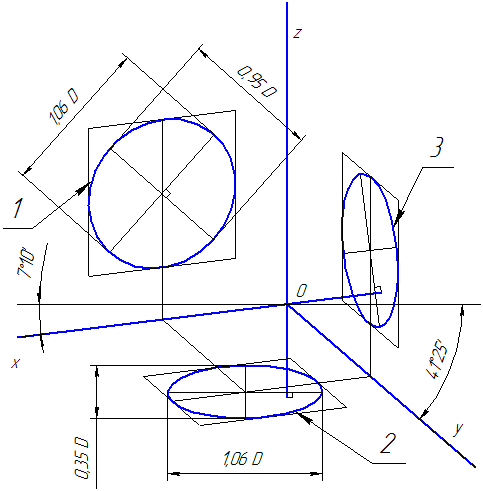
4.2.1 Фронтальная диметрическая проекция

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

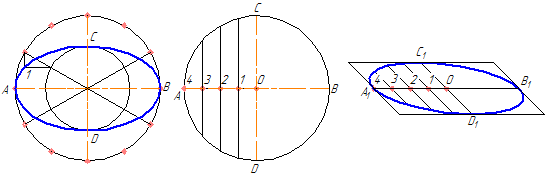
4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

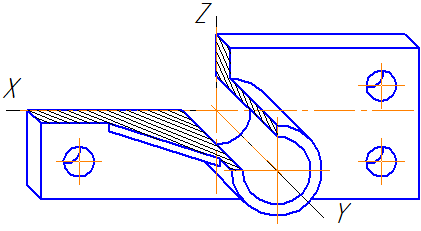
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Источник

Что означает изометрия в черчении

Как начертить изометрию?

Практически все, кому довелось изучать черчение и инженерную графику сталкивались с необходимостью произвести построение изометрической проекции детали. В этом уроке мы попробуем разобрать основные моменты, которые нужно знать, чтоб начертить изометрию. Уверен, что повторив указанные в этом уроке шаги, вы сможете самостоятельно выполнить и более сложное задание. В вашей детали может быть большее количество построений, но основные принципы останутся неизменными. Но при этом оговорюсь, что построение изометрии скорее всего будет вам не под силу, если вы еще не освоили построение третьего вида и построение простого разреза. Вы должны уже уметь хорошо ориентироваться в трех видах на чертеже.

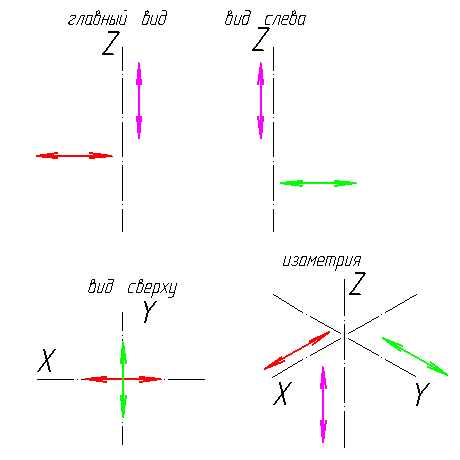
Начнем с того, что определимся с направлением осей в изометрии.

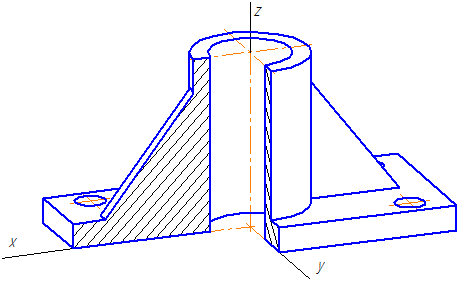
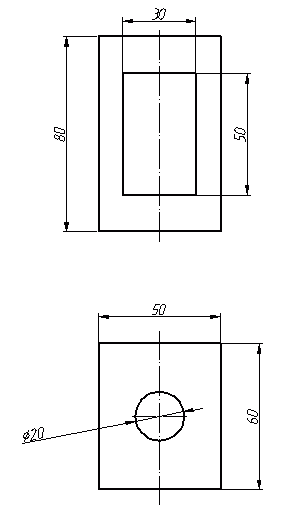
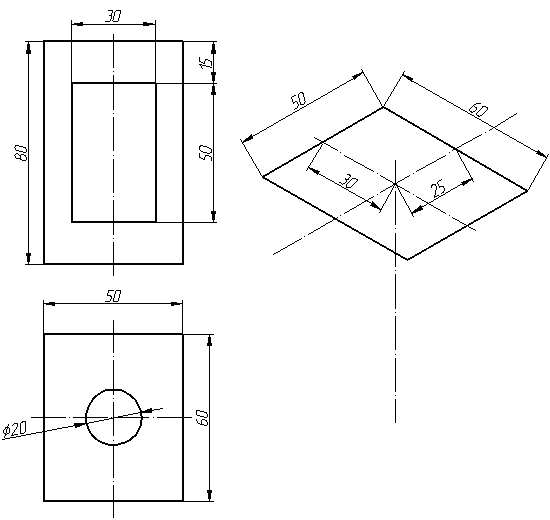
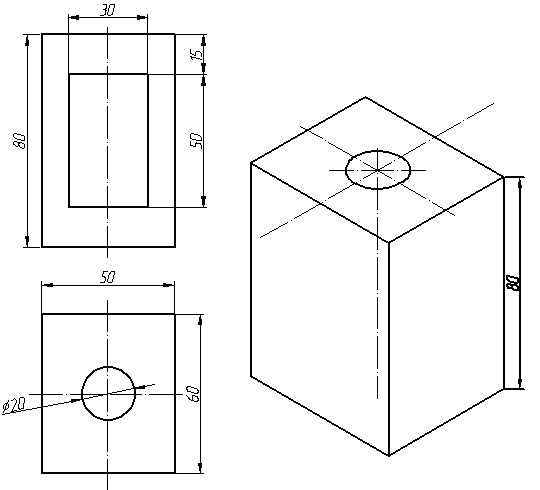
На этом закончим вступительную часть и начнем непосредственно построение изометрической проекции детали. Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.

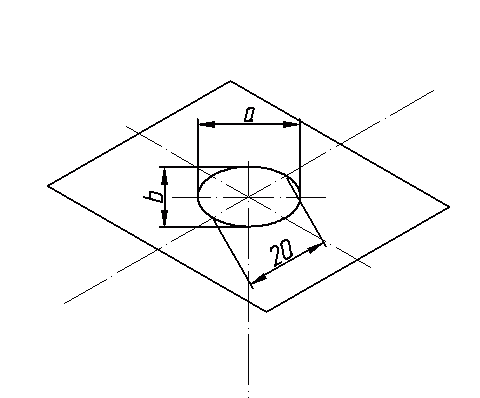
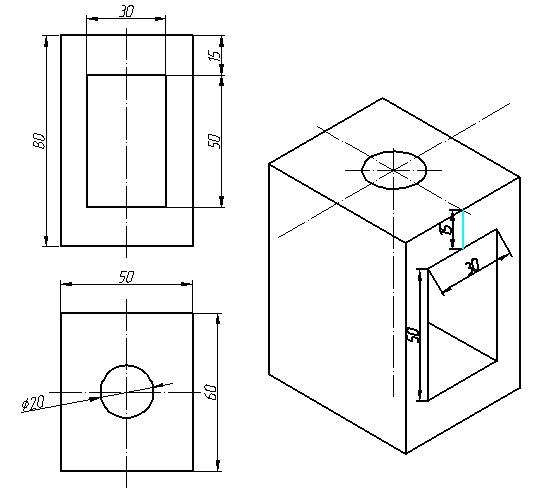
Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.

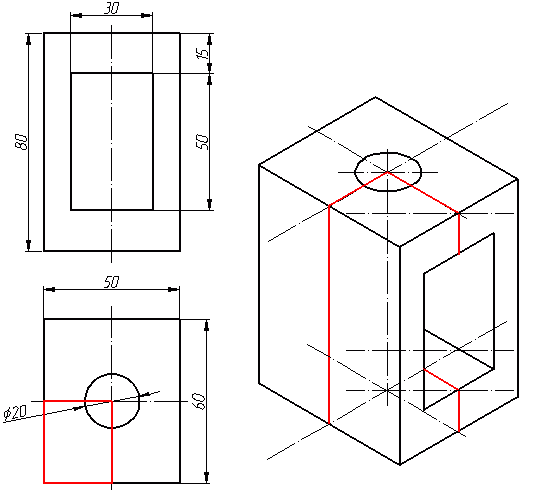
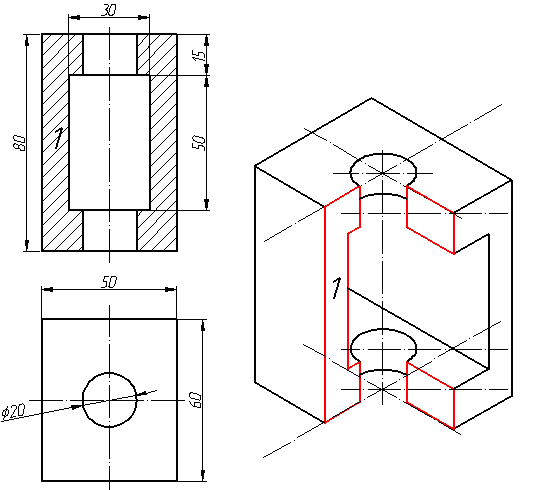
Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).

Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!

Следующий шаг в черчении: Уникальный урок на тему «Как начертить диметрию детали?»

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

Автор комментария: светка
Дата: 2010-09-08

пипец. я ни чего не понимаю. а завтра экзамен. ((((
Мы стараемся. Правда. Но в то же время мы понимаем, что написать понятно для всех не сможем. Что поделаешь. Однако, мы стремимся оформлять статьи по начертательной геометрии, а так же статьи по инженерной графике в максимально информативном и доступном виде.

Автор комментария: гринкс
Дата: 2010-09-28

хорошо что у меня завтра не экзамен. а лишь занятие по черчению. Со второго прочтения разобрался и смог начертить изометрию своей детали, надеюсь что правильно :))) Спасибо

Автор комментария: Антон
Дата: 2010-10-14

В музыкальном колледже требуют изометрический чертёж.Я бы лучше концерт сыграл.Черчение для меня-полная тьма.

Да уж. Неисповедимы пути. Я бы тоже концерт сыграл. Но вот к сожалению черчу лучше, чем музицирую. Не отчаивайтесь! Звоните, если не разберетесь. Удачи! Антон.

Автор комментария: Елена
Дата: 2010-10-21

замечательно.всё так понятно и просто

Автор комментария: Андрес
Дата: 2010-11-28

Огромное вам спасибо, вспомнил азы=)

Автор комментария: Диана
Дата: 2011-11-25

помогите начертить изометрию

Автор комментария: Диана
Дата: 2011-11-25

Антон спасибо большое за внимание. я уже все поняла. а вы физику хорошо знаете??

Автор комментария: оля
Дата: 2012-02-17

Автор комментария: михаил
Дата: 2012-06-09

Автор комментария: Андрей
Дата: 2012-06-19

Автор комментария: Виктор
Дата: 2012-09-15

Спасибо, что напомнил. Я сто лет уже изометрию не чертил, хотя и работаю инженером

Автор комментария: Яна
Дата: 2012-11-18

надо ли чертить все отверстия если они одинаковые? например 5 отверстий под винты. Или достаточно обозначить их оси?
На учебные чертежи нет ГОСТов. Есть разрешенные допущения. И их количество в каждом ВУЗе свое. В вашем случае правильным будет согласовать с преподавателем, либо выполнить все отверстия.

Автор комментария: Свелана
Дата: 2012-11-19

Статья отличная,большое спасибо, всё прояснилось) Скажите, вы писали выше в коментариях, что нужно сделать изометрию детали средней сложности, не появилась ещё?

Светлана, все произошло немного по-другому. Я взял среднюю деталь, имеющую несколько окружностей в своих формах и создал по ней урок. «Как начертить диметрию?» :))) Ссылка на него находится в самом конце статьи, до комментариев. Я считаю, что он может серьезно углубить ваши знания в части понимания, как чертить аксонометрические проекции разных деталей.

Автор комментария: 9th
Дата: 2012-12-26

Офигенно. Спасибо, с первого раза всё понял.

Автор комментария: Семен
Дата: 2013-02-10

Вы маги чтоль? как вы смогли обьяснить столь бестолковому человеку такую не простую вещь?))

Автор комментария: Александр
Дата: 2013-03-03

Ребят спасибо! Объяснено очень доходчиво, более лучшего объяснения не встречал!

Хорошо, коль так! Учитесь на здоровье!

СпасиБо! Можно двигаться дальше благодаря Вам! Появился свет в конце тоннеля!;)))

Автор комментария: Кирюха
Дата: 2013-03-17

Спасибо, все отлично написано, понятно. Особый респект автору. Еще хотелось бы узнать как показать резбу на валу в изометрической проекции.

Автор комментария: Лена
Дата: 2013-04-21

Спасибо большое. Все очень ясно изложено)

Автор комментария: Ольга
Дата: 2013-05-05

Спасибо огромное. Теперь все стало понятно, и я начертила деталь по контрольной.

Автор комментария: Серёга
Дата: 2013-06-02

Спасибо, что-то понял.

Автор комментария: MARUFJN
Дата: 2013-07-20

Автор комментария: АЙОГА
Дата: 2014-02-20

Автор комментария: Пётр
Дата: 2014-02-28

Скажите пожалуйста это в каком учебном заведении ещё есть черчение Я учусь в техническом Вузе и черчения нету

Автор комментария: Татьяна
Дата: 2014-03-13

Спасибо вам большое,очень помогли,без вашего урока бы не справилась,все объяснено доходчиво и по существу,очень благодарна)))

Татьяна, спасибо за отклик! Самому кажется, что все сделано хорошо, но вдруг только кажется? Ведь нет-нет, да приходят сообщения о непонятном изложении материала. Но я себя уговариваю, что это исключения, подтверждающие правило 🙂

Автор комментария: Вита
Дата: 2014-05-15

очень хорошая статья, не могли бы вы добавить изометрию шестиугольной призмы?очень надо!

Автор комментария: Марина
Дата: 2014-05-21

Большое спасибо. Знаю автокад для геологии, а черчение для меня вообще Луна, в вузе не было. Но благодаря объяснениям смогла сделать. Побольше бы таких толковых авторов. Еще раз огромное спасибо, спасли мне оценки ребенка

Автор комментария: Хама
Дата: 2014-11-04

Туфта! Размеры граней откладываются с коэффициентом 0,82 сторона не 50 мм а уже будет 0,82*50=41 хаваете инфу за должное.

ОК, расшифрую замечание внимательного читателя. В прямоугольной изометрической проекции действительные искажения по осям (по всем трем) и в самом деле равны 0,82. Но поскольку мы не оторваны от земли, и разбираемся с тем, как начертить домашнее задание, а не пишем реферат по черчению (!), то мы используем приведенные коэффициенты, равные единице. Я за 18 лет практики не встречал ни одного ВУЗа в нашей стране, где бы требовались коэффициенты 0,82. Поэтому рисуем с коэффициентом искажения по осям 1, но для энциклопедических знаний запоминаем 0,82. Не исключено, что этот вопрос когда-то будет задан в какой-нибудь телевикторине.

Автор комментария: Алексей
Дата: 2014-12-22

Начертите изометрию куба со стороной 80 мм и в каждой видимой гране впишите овал

Автор комментария: Антон
Дата: 2014-12-24

Огромное спасибо. Чудесное объяснение. Даже я понял. 🙂

Автор комментария: Человек
Дата: 2015-01-15

Автор комментария: Альбина
Дата: 2015-02-08

Большое спасибо, очень помогли! Сыну нужно было начертить изометрию, на уроке ничего не понял, я уже все забыла. Вместе с ним разобрались благодаря вашим объяснениям, очень доступно.

Автор комментария: Денис
Дата: 2015-03-11

Нужно ли заштриховывать ребро жесткости при сечении?

Денис, в изометрии всегда штрихую разрез вне зависимости от того, идет ли он через ребро жесткости. Так учили меня в свое время на кафедре черчения. Я готов предположить, что кто-то из преподавателей в каком-либо ВУЗе может считать иначе. В любом случае, стереть тонкие линии штриховки не составит труда. Но скорее всего стирать их не придется.

Автор комментария: Дмитрий
Дата: 2015-04-15

Очень бы хотелось видеть данный урок в pdf или doc формате. А в общем спасибо за урок!

Автор комментария: николай
Дата: 2015-11-17

Пользуйтесь на здоровье!

Автор комментария: Асхат Сабен
Дата: 2015-11-27

Я учусь в 9 классе. У нас есть урок черчения. Я №1 в классе по ЧЕРЧЕНИЯ! Я хочу стать архитектором. По этому я хочу узнать все подробности.

Автор комментария: Михаил
Дата: 2015-11-30

Автор комментария: Анатолий
Дата: 2015-12-01

Это не изометрия, а аксонометрия.Есть ещё и диметрия.

Автор комментария: Михаил
Дата: 2015-12-09

Ваш сайт первый по запросу в гугле. Что ж, совсем не зря! И разобрали как раз мой вариант. Спасибо за вашу работу!

Вот это я понимаю, вот это повезло 🙂 А ведь деталь из головы брал! Но, как я понимаю, вы еще и суть теперь знаете, а это очень хорошо! Да, не зря я работал над оптимизацией, не зря!

Автор комментария: Сергей
Дата: 2016-01-10

Здравствуйте! А моему мнению,в чертеже с вырезанной четвертью, допущена неточность!

Сергей, приветствую! На картинке с вырезанной четвертью наверняка есть «неточности». Например нет штриховки, какие-то разноцветные линии, торчащие не по ГОСТу осевые. Но урок-то был о другом. Пусть пока остается как есть.

Автор комментария: Светлана
Дата: 2016-04-27

Спасибо, всё поняла (хотя черчение проходила в школе лет 40 назад))). Сейчас помогаю сыну. Предлагаю и Вам помощь: редактировать тексты перед публикацией на предмет знаков препинания (для лучшего понимания такой полезной информации!). С уважением! Успехов.

Автор комментария: Зоя
Дата: 2016-12-16

Давно уже не чертила изометрию, все забыла. Благодарю за отличный урок!

Автор комментария: Дан
Дата: 2017-01-08

Спасибо за это объяснение, лично мне аксанометрия нравится, но в отверстиях на плоскости малек туплю,блин архитектору это нужно. Спасибо вам)

Автор комментария: Азиз
Дата: 2018-01-09

Спасибо за объяснение,все четко показано

Автор комментария: Варвара
Дата: 2018-04-27

Спасибо огромное. Учителя объясняют тему не понятно, а здесь всё ясно и понятно

Автор комментария: Дмитрий
Дата: 2018-05-12

Спасибо большое! Хоть вспомнил правила изометрии. А то работаю авиационным инженером, завтра самолет строить, а я позабыл изометрические коэффициенты)))

Автор комментария: виктор
Дата: 2018-09-23

Автор комментария: жопа
Дата: 2018-09-23

такая себе хорактеристика азаметрий

Автор комментария: Андрей
Дата: 2019-07-10

Я, конечно, изучал изометрию почти 15 лет назад, но у Вас в финальном чертеже с разрезом есть ошибка. По условиям вертикальное отверстие сквозное, а на чертеже сделано не правильно. У вас это отверстие «уходит» дальше размеров самой детали. Как-то так.

Автор комментария: Андрей
Дата: 2019-07-10

Поправочка: всё правильно. Совпадают вертикальные линии задней стенки с разрезом. Изометрия такая изометрия. Пока не измерил в живую, не увидел. Конечно перспектива в этом плане более информативна.

Автор комментария: Владимир
Дата: 2020-07-31

ого, я уже забыл все что мы проходили на уроках черчения в школе, оказывается.

Автор комментария: LeOn4iK
Дата: 2020-11-15

Очень круто, мне понравилось!

Автор комментария: Александр
Дата: 2021-03-20

Сам учился в строительном, со временем что-то забывается, 30 лет прошло. Для детей и внуков приходится заглядывать. БлагоДарствую за толковое разъяснение, даже для школьников

Автор комментария: Waffenträger auf E 100
Дата: 2021-08-07

Бро, это было 11 лет назад.

Добавьте свой комментарий:

Наша страница в ВК:

Источник