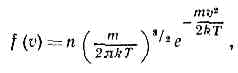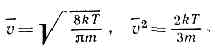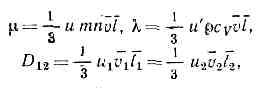Что означает кинетическая теория

Кинетическая теория газов

Полезное

Смотреть что такое «Кинетическая теория газов» в других словарях:

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — раздел теор. физики, исследующий св ва газов статистич. методами на основе представления об их мол, строении и определ. законе вз ствия между молекулами. Обычно к К. т. г. относят лишь теорию неравновесных св в газов, теория же их равновесных св… … Физическая энциклопедия

Кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом взаимодействующих между собой, с внешними полями и ограничивающими поверхностями. К. т. г. изучает неравновесные… … Энциклопедия техники

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — раздел физики, изучающий свойства газов статистич. методами на основе представлений об их молекулярном строении и определ. законе взаимодействия между молекулами. Обычно к К. т. г. относят лишь теорию неравновесных свойств газов. Осн. объекты… … Физическая энциклопедия

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — раздел теоретической физики, исследующий свойства газов статистическими методами и объясняющий свойства газов на основе их молекулярного строения, а также законов непрерывного движения и взаимодействия молекул (атомов). К. т. г. рассматривает… … Большая политехническая энциклопедия

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — объясняет неравновесные свойства газов (явления переноса энергии, массы, импульса) на основе законов движения и взаимодействия молекул … Большой Энциклопедический словарь

кинетическая теория газов — объясняет неравновесные свойства газов (явления переноса энергии, массы, импульса) на основе законов движения и взаимодействия молекул. * * * КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ, раздел физики, изучающий свойства газов методами… … Энциклопедический словарь

кинетическая теория газов — kinetinė dujų teorija statusas T sritis fizika atitikmenys: angl. gas kinetic theory; kinetic theory of gases vok. kinetische Gastheorie, f rus. кинетическая теория газов, f pranc. théorie cinétique des gaz, f … Fizikos terminų žodynas

Кинетическая теория газов — Сущность ее может быть выражена в немногих словах. Согласно этой теории, газы состоят из огромного числа отдельных весьма малых частиц, двигающихся по всем возможным направлениям и со всеми возможными скоростями; частицы эти связаны между собой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

кинетическая теория газов — Зависимость интенсивности испарения от плотности пара над стенкой. кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом… … Энциклопедия «Авиация»

кинетическая теория газов — Зависимость интенсивности испарения от плотности пара над стенкой. кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом… … Энциклопедия «Авиация»

кинетическая теория газов — Зависимость интенсивности испарения от плотности пара над стенкой. кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом… … Энциклопедия «Авиация»

Источник

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ

Полезное

Смотреть что такое «КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ» в других словарях:

Кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом взаимодействующих между собой, с внешними полями и ограничивающими поверхностями. К. т. г. изучает неравновесные… … Энциклопедия техники

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — раздел физики, изучающий свойства газов статистич. методами на основе представлений об их молекулярном строении и определ. законе взаимодействия между молекулами. Обычно к К. т. г. относят лишь теорию неравновесных свойств газов. Осн. объекты… … Физическая энциклопедия

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — раздел теоретической физики, исследующий свойства газов статистическими методами и объясняющий свойства газов на основе их молекулярного строения, а также законов непрерывного движения и взаимодействия молекул (атомов). К. т. г. рассматривает… … Большая политехническая энциклопедия

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ — объясняет неравновесные свойства газов (явления переноса энергии, массы, импульса) на основе законов движения и взаимодействия молекул … Большой Энциклопедический словарь

кинетическая теория газов — объясняет неравновесные свойства газов (явления переноса энергии, массы, импульса) на основе законов движения и взаимодействия молекул. * * * КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ, раздел физики, изучающий свойства газов методами… … Энциклопедический словарь

кинетическая теория газов — kinetinė dujų teorija statusas T sritis fizika atitikmenys: angl. gas kinetic theory; kinetic theory of gases vok. kinetische Gastheorie, f rus. кинетическая теория газов, f pranc. théorie cinétique des gaz, f … Fizikos terminų žodynas

Кинетическая теория газов — Сущность ее может быть выражена в немногих словах. Согласно этой теории, газы состоят из огромного числа отдельных весьма малых частиц, двигающихся по всем возможным направлениям и со всеми возможными скоростями; частицы эти связаны между собой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

кинетическая теория газов — Зависимость интенсивности испарения от плотности пара над стенкой. кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом… … Энциклопедия «Авиация»

кинетическая теория газов — Зависимость интенсивности испарения от плотности пара над стенкой. кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом… … Энциклопедия «Авиация»

кинетическая теория газов — Зависимость интенсивности испарения от плотности пара над стенкой. кинетическая теория газов — раздел физики, изучающий явления в газах статистическими методами, рассматривающий газ как совокупность молекул, заданным образом… … Энциклопедия «Авиация»

Источник

Молекулярно-кинетическая теория строения вещества

Содержание:

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химического вещества. В основе молекулярно-кинетической теории лежат три основных положения:

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Молекулярно-кинетическая теория строения вещества

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.

В основе молекулярно-кинетической теории лежат три основных положения:

Основные положения молекулярно-кинетической теории

При наблюдениях за явлениями природы, а также при изучении свойств различных видов вещества наше воображение поражает необыкновенное многообразие видов вещества и различие его свойств. Почему свойства вещества так разнообразны, можно понять, если изучить его внутреннее строение.

В начале прошлого столетия английский ученый Д. Дальтон показал, что многие закономерности явлений природы можно объяснить, используя представления об атомах и молекулах, и научно обосновал молекулярное строение вещества. К началу нашего столетия была окончательно создана и подтверждена множеством опытов молекулярно-кинетическая теория строения вещества. В чем же заключается сущность этой теории?

Всякое вещество состоит из молекул (от латинского «мо-лес» — масса, «кула» — уменьшительный суффикс). Молекулой называют наименьшую частичку вещества, способную к самостоятельному существованию и сохраняющую химические свойства этого вещества.

Молекулы состоят из атомов (от греческого «атомос» — неделимый); например, молекула воды состоит из двух атомов водорода и одного атома кислорода, это записывают так: Н₂0. Если при каком-либо явлении природы молекулы остаются неизменными, то вещество сохраняет свои химические свойства. Если же молекулы изменяют свое строение или распадаются на отдельные атомы, то получаются новые виды вещества с другими химическими и физическими свойствами. Например, молекулы воды можно разложить на атомы водорода и кислорода. Тогда вместо воды получаются газы водород и кислород. Попытки химически разложить эти газы на более простые вещества не увенчались успехом.

Такие вещества, которые нельзя разложить на более простые составные части, называются химическими элементами, например: кислород, азот, свинец и т. д. Каждому химическому элементу соответствуют атомы, которые имеют определенное место (определенный номер) в таблице Менделеева. Соединение атомов в группу образует молекулу вещества. Совокупность одинаковых молекул составляет определенный вид вещества. Химические и физические свойства этого вещества определяются числом и видом атомов в его молекулах.

Свойства вещества зависят также от внутреннего расположения атомов относительно друг друга. Например, графит и алмаз состоят из атомов углерода и с точки зрения их внутреннего строения отличаются только относительным расположением этих атомов. Между тем физические свойства этих веществ резко отличаются друг от друга: алмаз обладает большой твердостью, прозрачен для лучей света, очень хороший изолятор, а графит — очень мягкий, непрозрачный материал, проводник.

Наконец, свойства вещества определяются еще и внешними условиями. Все это обусловлено тем, что молекулы и атомы всегда взаимодействуют друг с другом и обладают химической энергией. Именно движением и взаимодействием атомов и молекул объясняется все неисчерпаемое разнообразие огромного большинства наблюдаемых нами явлений природы.

Сформулируем основные положения молекулярно-кинетической теории строения вещества.

Вспомним некоторые явления, подтверждающие эти положения.

Как показывает опыт, все газы легко сжимаемы. Это доказывает, что между молекулами газа имеются значительные свободные промежутки. Жидкости и твердые тела также сжимаемы, но значительно меньше, чем газы. Это означает, что в жидкостях и твердых телах также имеются межмолекулярные промежутки, но они значительно меньше, чем в газах.

В результате взаимного проникновения молекул одного вещества между молекулами другого вещества происходит смешивание различных газов или жидкостей, растворение твердых тел в жидкостях, испарение жидкостей и твердых тел.

Стремление молекул газа занять весь предоставленный ему объем показывает, что молекулы газа находятся в непрерывном хаотическом движении.

Хаотическое движение молекул часто называют тепловым, так как оно тесно связано с понятием температуры: чем выше температура тела, тем интенсивнее тепловое движение его молекул, тем больше кинетической энергии приходится в среднем на одну его молекулу. Поскольку кинетическая энергия пропорциональна квадрату скорости движения, то при нагревании тела средняя скорость движения его молекул увеличивается, а при охлаждении — уменьшается.

Следует отметить, что явления, изучаемые в молекулярной физике, определяются движением и взаимодействием огромного числа молекул; поэтому для описания таких явлений пользуются только средними значениями величин, характеризующих молекулярный мир.

Диффузия

Одно из распространенных явлений природы, которое объясняют хаотическим движением молекул, представляет собой явление диффузии (от латинского «диффузио» — растекание). Примером диффузии служит распространение запаха цветов или приготовляемой пищи. Вследствие испарения концентрация молекул пахучих веществ в непосредственной близости от букета цветов большая, а хаотическое тепловое движение молекул перемешивает молекулы воздуха и пахучих веществ, что и вызывает распространение запаха по всей комнате. Такое перемешивание ведет к выравниванию концентрации молекул пахучих веществ во всем объеме комнаты.

Процесс выравнивания концентрации молекул какого-либо вещества в пространстве, обусловленный хаотическим движением молекул, называется диффузией. Поскольку средняя скорость хаотического движения молекул возрастает при повышении температуры, то и диффузия должна ускоряться при повышении температуры, что действительно подтверждается всеми опытами.

В жидкостях диффузия протекает значительно медленнее, чем в газах. Если налить в сосуд чистую воду, а сверху подкрашенный спирт так, чтобы между жидкостями была видна резкая граница, и наблюдать за ней, то через несколько дней мы увидим, что резкая граница исчезла, а вода окрасилась на значительную глубину вследствие взаимной диффузии воды и спирта. (Подумайте, почему этот опыт нельзя объяснить действием силы тяжести.)

В твердых телах диффузия происходит очень медленно и заметна лишь при повышенной температуре. Если плотно прижать друг к другу две разнородные металлические пластинки и держать их при температуре в несколько сот градусов, то взаимная диффузия металлов будет заметна уже через несколько часов. Это можно обнаружить, если разделить пластинки и исследовать их поверхности.

Почему же диффузия в жидкостях протекает медленнее, чем в газах, а в твердых телах медленнее, чем в жидкостях? Очевидно, это объясняется тем, что в жидкостях молекулы расположены ближе друг к другу, чем в газах, и силы взаимного притяжения молекул замедляют процесс диффузии. Поскольку в твердых телах молекулярные силы больше, чем в жидкостях, процесс диффузии в твердых телах протекает еще медленнее.

Силы молекулярного взаимодействия

При изучении строения вещества было установлено, что в состав любых молекул входят как положительные, так и отрицательные электрические заряды. Так как одноименные заряды отталкиваются, а разноименные притягиваются, то между молекулами одновременно действуют силы притяжения и силы отталкивания. Кроме того, между движущимися зарядами атомов и молекул имеется магнитное взаимодействие, которое дает свой вклад в равнодействующую сил притяжения и отталкивания молекул.

В твердых телах молекулярные силы проявляют себя как силы упругости при различного рода деформациях и как силы, обусловливающие прочность тела. Эти силы действуют только на очень малых расстояниях. Поэтому, например, прижимая друг к другу осколки разбитой фарфоровой чашки, нельзя получить целую чашку, так как расстояние между огромным большинством молекул в щели оказывается настолько большим, что силы молекулярного взаимодействия между ними не возникают. Однако если взять мягкий материал, то сжатием можно сблизить на нужное расстояние большое число молекул. Тогда прижатые друг к другу части тела сцепятся настолько прочно, что их будет трудно разъединить. Так, можно прочно сцепить свинцовые стержни, прижав их друг к другу зачищенными плоскими поверхностями. При площади поверхности в 1 см 2 сцепленные стержни выдерживают гирю массой 5 кг. (Продумайте, на чем основано сваривание и склеивание твердых тел.)

Силы взаимодействия возникают при сближении двух любых молекул, как однородных, так и разнородных, а величина этих сил зависит от природы молекул.

На рис. 2.1, а изображен типичный график зависимости равнодействующей F_p сил притяжения и отталкивания двух молекул А и В от расстояния r между их центрами.

При построении графика силы отталкивания молекул F_от считают положительными, а силы притяжения F_пр — отрицательными.

Расстояние r₀ соответствует положению устойчивого равновесия молекул, так как равнодействующая молекулярных сил в этом случае равна нулю. При изменении расстояния между молекулами возникают силы, возвращающие молекулы в прежнее положение. Действительно, на графике видно, что при сближении молекул преобладают силы отталкивания (положительные), а при удалении — силы притяжения (отрицательные).

Наименьшее расстояние между молекулами, на котором силы взаимодействия молекул так малы, что ими можно пренебречь, называется радиусом молекулярного действия

Кинетическая и потенциальная энергия молекул

Если массу молекулы тела обозначить т, а скорость ее поступательного движения , то кинетическая энергия поступательного движения молекулы будет равна:

где N — общее число молекул в теле. Если все молекулы одинаковы, то

Здесь обозначает среднюю квадратичную скорость хаотического движения молекул:

Поскольку между молекулами имеются силы взаимодействия, то молекулы тела, кроме кинетической энергии, обладают потенциальной энергией. Будем считать потенциальную энергию уединенной молекулы, не взаимодействующей с другими молекулами, равной нулю. Тогда при взаимодействии двух молекул потенциальная энергия, обусловленная силами отталкивания, будет положительной, а силами притяжения — отрицательной (рис. 2.1, б), поскольку при сближении молекул для преодоления сил отталкивания надо выполнить определенную работу, а силы притяжения, наоборот, сами совершают работу. На рис. 2.1, б показан график изменения потенциальной энергии взаимодействия двух молекул в зависимости от расстояния r между ними. Часть графика потенциальной энергии вблизи ее наименьшего значения называют потенциальной ямой, а величину наименьшего значения энергии П_мин — глубиной потенциальной ямы.

При отсутствии кинетической энергии (Е_пост = 0) молекулы расположились бы на расстоянии r₀, которое соответствует их устойчивому равновесию, так как равнодействующая молекулярных сил в этом случае равна нулю (рис. 2.1, а), а потенциальная энергия минимальна. Чтобы удалить друг от друга молекулы, нужно совершить работу по преодолению сил взаимодействия молекул, равную по величине П_мин (другими словами, молекулы должны преодолеть потенциальный барьер высотой П_мин).

Так как в действительности молекулы всегда обладают кинетической энергией, то расстояние между ними непрерывно изменяется и может быть как больше, так и меньше r₀. Если кинетическая энергия молекулы В будет меньше П_мин, например Е_пост1 на рис. 2.1, б, то молекула будет двигаться в пределах потенциальной ямы. Преодолевая противодействие сил притяжения (или отталкивания), молекула В может удаляться от А (или сближаться) до расстояний, при которых вся ее кинетическая энергия Е_пост1 превращается в потенциальную энергию взаимодействия. Эти крайние положения молекулы определяются точками на потенциальной кривой на уровне Е_пост1 от дна потенциальной ямы (рис. 2.1, б). Затем силы притяжения (или отталкивания) отбрасывают молекулу В от этих крайних положений. Таким образом, силы взаимодействия удерживают молекулы друг возле друга на некотором среднем расстоянии .

Если кинетическая энергия молекулы В больше П_мин (Е_пост1 на рис. 2.1, б), то она преодолеет потенциальный барьер и расстояние между молекулами может возрастать неограниченно.

Когда молекула движется в пределах потенциальный ямы, то чем больше ее кинетическая энергия (Е_пост1, Е_пост2 на рис. 2.1, б), т. е. чем выше температура тела, тем больше становится среднее расстояние между молекулами (r₁, r₂). Этим объясняется расширение твердых тел и жидкостей при нагревании.

Увеличение среднего расстояния между молекулами объясняется тем, что график потенциальной энергии слева от П_мин поднимается гораздо круче, чем справа. Такая асимметрия графика получается вследствие того, что силы отталкивания уменьшаются при увеличении r значительно быстрее, чем силы притяжения (рис. 2.1, а).

Агрегатное состояние вещества

Изучение свойств вещества показало, что одно и то же вещество может встречаться в твердом, жидком и газообразном состояниях, которые часто называют агрегатными состояниями, например: лед, вода и водяной пар.

Вспомним, что свойства вещества зависят от движения его молекул и от сил взаимодействия между ними. Силы молекулярного взаимодействия стремятся удержать молекулы на определенных расстояниях друг от друга, а хаотическое движение молекул стремится разбросать их по всему пространству. Совместное действие этих двух факторов и определяет агрегатное состояние каждого вещества.

Рассмотрим потенциальную кривую двух молекул (рис. 2.1, б). Пока кинетическая энергия поступательного движения молекулы Е_пост мала, молекула совершает колебательное движение в пределах потенциальной ямы. Ее кинетическая энергия при этом переходит в потенциальную энергию взаимодействия, и обратно. Молекулы тела могут иметь различные скорости и величину Е_пост, но пока среднее значение кинетической энергии молекул много меньше П_мин, молекулы только колеблются около своих средних положений и вещество остается в твердом состоянии.

Когда в результате нагревания тела энергия увеличивается и оказывается по величине близкой к П_мин , вещество становится жидким: те молекулы, у которых Е_пост

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Кинетическая теория газов

Содержание

История [ править ]

Предположения [ править ]

Теория идеальных газов делает следующие предположения:

Таким образом, динамику движения частицы можно рассматривать классически, а уравнения движения обратимы во времени.

Свойства равновесия [ править ]

Давление и кинетическая энергия [ править ]

Частица сталкивается с одной конкретной боковой стенкой один раз за

Общая сила на стене составляет

где черта обозначает среднее значение по N частицам.

Поскольку движение частиц является случайным и нет смещения в каком-либо направлении, средний квадрат скорости в каждом направлении идентичен:

По теореме Пифагора в трех измерениях полный квадрат скорости v определяется выражением

а силу можно записать как:

По кинетической энергии газа K :

Температура и кинетическая энергия [ править ]

что приводит к упрощенному выражению средней кинетической энергии на молекулу [15]

1 2 m v 2 ¯ = 3 2 k B T <\displaystyle \displaystyle <\frac <1><2>>m<\overline >>=<\frac <3><2>>k_T> .

Таким образом, произведение давления и объема на моль пропорционально средней (поступательной) молекулярной кинетической энергии.

Двухатомные газы должны иметь 7 степеней свободы, но более легкие двухатомные газы действуют так, как будто они имеют только 5. Одноатомные газы имеют 3 степени свободы.

Таким образом, кинетическая энергия на кельвин (одноатомный идеальный газ ) равна 3 [R / 2] = 3R / 2:

При стандартной температуре (273,15 К) получаем:

Столкновения с контейнером [ править ]

Распределение скорости частиц, ударяющихся о стенку контейнера, можно рассчитать [17] на основе наивной кинетической теории, и результат может быть использован для анализа скорости эффузивного потока :

n v cos ⁡ θ d A d t × ( m 2 π k B T ) 3 2 e − m v 2 2 k B T ( v 2 sin ⁡ θ d v d θ d ϕ ) <\displaystyle nv\cos <\theta >\,dAdt<\times >\left(<\frac <2\pi k_T>>\right)^<\frac <3><2>>e^<-<\frac ><2k_T>>>(v^<2>\sin <\theta >\,dvd\phi )> .

Эта величина также известна как «скорость столкновения» в физике вакуума.

В сочетании с законом идеального газа это дает:

Распределение скоростей частиц, попадающих в эту небольшую область:

Скорость молекул [ править ]

Из формулы кинетической энергии можно показать, что

Свойства транспорта [ править ]

Вязкость и кинетический импульс [ править ]

n v cos ⁡ θ d A d t × ( m 2 π k B T ) 3 / 2 e − m v 2 2 k B T ( v 2 sin ⁡ θ d v d θ d ϕ ) <\displaystyle nv\cos <\theta >\,dAdt<\times >\left(<\frac <2\pi k_T>>\right)^<3>\,e^<-<\frac ><2k_T>>>(v^<2>\sin <\theta >\,dvd\phi )>

Интегрирование по всем подходящим скоростям в пределах ограничения

дает прямую передачу импульса в единицу времени на единицу площади (также известную как напряжение сдвига ):

τ ± = 1 4 v ¯ n ⋅ m ( u 0 ± 2 3 l d u d y ) <\displaystyle \tau ^<\pm >=<\frac <1><4>><\bar >n\cdot m\left(u_<0>\pm <\frac <2><3>>l\,\right)>

Таким образом, чистая скорость количества движения на единицу площади, переносимого по воображаемой поверхности, равна

τ = τ + − τ − = 1 3 v ¯ n m ⋅ l d u d y <\displaystyle \tau =\tau ^<+>-\tau ^<->=<\frac <1><3>><\bar >nm\cdot l\,>

Комбинируя приведенное выше кинетическое уравнение с законом вязкости Ньютона

дает уравнение для вязкости сдвига, которое обычно обозначают, когда речь идет о разреженном газе: η 0 <\displaystyle \eta _<0>>

Объединение этого уравнения с уравнением для длины свободного пробега дает

η 0 = 1 3 2 m ⋅ v ¯ σ <\displaystyle \eta _<0>=<\frac <1><3<\sqrt <2>>>><\frac >><\sigma >>>

Распределение Максвелла-Больцмана дает среднюю (равновесную) скорость молекул как

v ¯ = 2 π v p = 2 2 π ⋅ k B T m <\displaystyle <\bar >=<\frac <2><\sqrt <\pi >>>v_

=2<\sqrt <<\frac <2><\pi >>\cdot <\frac T>>>>>>

k B ⋅ N A = R and M = m ⋅ N A <\displaystyle k_\cdot N_=R\quad <\text>\quad M=m\cdot N_>

и вставьте скорость в уравнение вязкости выше. Это дает хорошо известное уравнение сдвиговой вязкости для разреженных газов :

η 0 = 2 3 π ⋅ m k B T σ = 2 3 π ⋅ M R T σ ⋅ N A <\displaystyle \eta _<0>=<\frac <2><3<\sqrt <\pi >>>>\cdot <\frac <\sqrt T>><\sigma >>=<\frac <2><3<\sqrt <\pi >>>>\cdot <\frac <\sqrt ><\sigma \cdot N_>>>

σ = π ( 2 r ) 2 = π d 2 <\displaystyle \sigma =\pi \left(2r\right)^<2>=\pi d^<2>>

Теплопроводность и тепловой поток [ править ]

Следуя той же логике, что и выше, можно вывести кинетическую модель теплопроводности [18] разреженного газа:

n v cos ⁡ θ d A d t × ( m 2 π k B T ) 3 2 e − m v 2 2 k B T ( v 2 sin ⁡ θ d v d θ d ϕ ) <\displaystyle \quad nv\cos <\theta >\,dAdt<\times >\left(<\frac <2\pi k_T>>\right)^<\frac <3><2>>e^<-<\frac ><2k_T>>>(v^<2>\sin <\theta >\,dvd\phi )>

Интегрирование по всем подходящим скоростям в пределах ограничения

дает передачу энергии в единицу времени на единицу площади (также известную как тепловой поток ):

q y ± = − 1 4 v ¯ n ⋅ ( ε 0 ± 2 3 m c v l d T d y ) <\displaystyle \quad q_^<\pm >=-<\frac <1><4>><\bar >n\cdot \left(\varepsilon _<0>\pm <\frac <2><3>>mc_l\,

\right)>

q = q y + − q y − = − 1 3 v ¯ n m c v l d T d y <\displaystyle \quad q=q_^<+>-q_^<->=-<\frac <1><3>><\bar >nmc_l\,

>

Комбинируя приведенное выше кинетическое уравнение с законом Фурье

дает уравнение теплопроводности, которое обычно обозначают, когда речь идет о разреженном газе: κ 0 <\displaystyle \kappa _<0>>

κ 0 = 1 3 v ¯ n m c v l <\displaystyle \quad \kappa _<0>=<\frac <1><3>><\bar >nmc_l>

Коэффициент диффузии и диффузионный поток [ править ]

Следуя той же логике, что и выше, можно вывести кинетическую модель для массовой диффузии [18] разреженного газа:

n v cos ⁡ θ d A d t × ( m 2 π k B T ) 3 2 e − m v 2 2 k B T ( v 2 sin ⁡ θ d v d θ d ϕ ) <\displaystyle \quad nv\cos <\theta >\,dAdt<\times >\left(<\frac <2\pi k_T>>\right)^<\frac <3><2>>e^<-<\frac ><2k_T>>>(v^<2>\sin <\theta >\,dvd\phi )>

n ± = ( n 0 ± l cos ⁡ θ d n d y ) <\displaystyle \quad n^<\pm >=\left(n_<0>\pm l\cos \theta \,\right)>

Интегрирование по всем подходящим скоростям в пределах ограничения

дает молекулярный перенос в единицу времени на единицу площади (также известный как диффузионный поток ):

J y ± = − 1 4 v ¯ ⋅ ( n 0 ± 2 3 l d n d y ) <\displaystyle \quad J_^<\pm >=-<\frac <1><4>><\bar >\cdot \left(n_<0>\pm <\frac <2><3>>l\,\right)>

J = J y + − J y − = − 1 3 v ¯ l d n d y <\displaystyle \quad J=J_^<+>-J_^<->=-<\frac <1><3>><\bar >l>

Комбинируя приведенное выше кинетическое уравнение с первым законом диффузии Фика

дает уравнение для массовой диффузии, которое обычно обозначают, когда речь идет о разреженном газе: D 0 <\displaystyle D_<0>>

Источник