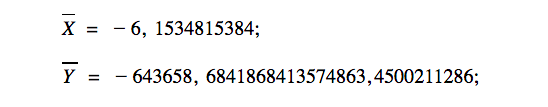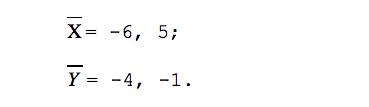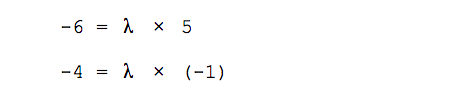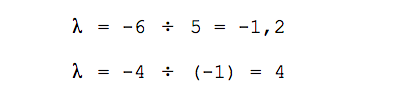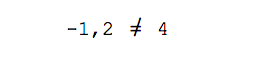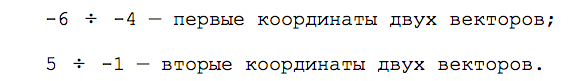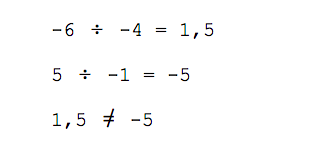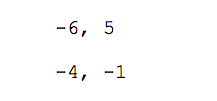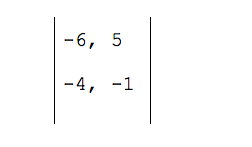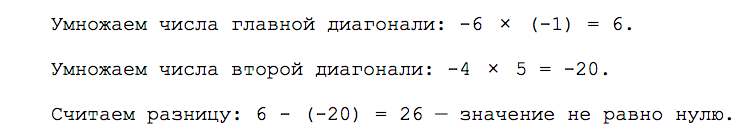Что означает коллинеарны в геометрии

Коллинеарные вектора

Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Содержание

Обозначения

Свойства коллинеарности

Пусть — векторы пространства . Тогда верны следующие утверждения:

Другие объекты

Выше описанные критерии коллинеарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле (а, например, как элементы произвольного линейного пространства).

Иногда коллинеарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной прямой.

См. также

Полезное

Смотреть что такое «Коллинеарные вектора» в других словарях:

Коллинеарные векторы — Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допустим, но не рекомендуется, синоним «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или… … Википедия

КОЛЛИНЕАРНЫЕ ВЕКТОРЫ — векторы, лежащие на одной прямой или на параллельных прямых. Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. Нулевой вектор коллинеарен всякому вектору. Аналогично,… … Математическая энциклопедия

Коллинеарность — Два коллинеарных противоположно направленных вектора Два ненулевых (не равных 0) вектора называются … Википедия

Вектор — направленный отрезок прямой, или отрезок, один из концов которого называется началом вектора, а другой его концом. Различают: 1) коллинеарные векторы, лежащие на одной прямой или на параллельных прямых; 2) компланарные векторы, лежащие в одной… … Начала современного естествознания

Источник

Коллинеарные векторы

В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.

Условия коллинеарности векторов

Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.

Два вектора коллинеарны, если выполняется одно из условий ниже:

2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.

3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).

Примеры задач

Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.

Задание 2
Выясним, при каком значении n векторы и коллинеарны.

Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.

Источник

Условие коллинеарности векторов

В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.

Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.

Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.

Координатная форма условия коллинеарности векторов

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Решение

Ответ: заданные векторы коллинеарны.

Решение

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7

Ответ: при p = 6 7 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Решение

Решение

Источник

Содержание

Очки на линии

В любой геометрии множество точек на прямой называется коллинеарен. В Евклидова геометрия это отношение интуитивно визуализируется точками, лежащими в ряд на «прямой линии». Однако в большинстве геометрий (включая евклидову) a линия обычно примитивный (неопределенный) тип объекта, поэтому такие визуализации не обязательно подойдут. А модель поскольку геометрия предлагает интерпретацию того, как точки, линии и другие типы объектов связаны друг с другом, и такое понятие, как коллинеарность, должно интерпретироваться в контексте этой модели. Например, в сферическая геометрия, где прямые представлены в стандартной модели большими окружностями сферы, а наборы коллинеарных точек лежат на одной большой окружности. Такие точки не лежат на «прямой линии» в евклидовом смысле и не считаются в ряд.

Отображение геометрии на себя, которое переводит линии в линии, называется коллинеация; он сохраняет свойство коллинеарности. В линейные карты (или линейные функции) из векторные пространства, рассматриваемые как геометрические карты, преобразовать линии в линии; то есть они сопоставляют наборы коллинеарных точек с наборами коллинеарных точек и, таким образом, являются коллинеатами. В проективная геометрия эти линейные отображения называются омографии и являются лишь одним из типов коллинеации.

Примеры в евклидовой геометрии

Треугольники

В любом треугольнике коллинеарны следующие множества точек:

Четырехугольники

Шестиугольники

Конические секции

Шишки

Тетраэдры

Алгебра

Коллинеарность точек, координаты которых заданы

имеет классифицировать 1 или меньше, точки лежат на одной прямой.

имеет классифицировать 2 или меньше, точки лежат на одной прямой. В частности, для трех точек на плоскости (п = 2), указанная выше матрица является квадратной, а точки коллинеарны тогда и только тогда, когда ее детерминант равно нулю; так как этот определитель 3 × 3 плюс или минус в два раза больше площадь треугольника с этими тремя точками в качестве вершин, это эквивалентно утверждению, что три точки коллинеарны тогда и только тогда, когда треугольник с этими точками в качестве вершин имеет нулевую площадь.

Коллинеарность точек, попарные расстояния которых заданы

Набор не менее трех различных точек называется прямой, что означает, что все точки коллинеарны тогда и только тогда, когда для каждых трех из этих точек А, B, и C, следующий определитель Определитель Кэли-Менгера равен нулю (с d(AB) означает расстояние между А и B, так далее.):

Этот детерминант определяется Формула Герона, равная −16 квадрату площади треугольника со сторонами d(AB), d(до н.э), и d(AC); поэтому проверка того, равен ли этот определитель нулю, эквивалентна проверке, есть ли у треугольника с вершинами А, B, и C имеет нулевую площадь (поэтому вершины лежат на одной прямой).

Эквивалентно, набор по крайней мере из трех различных точек коллинеарен тогда и только тогда, когда для каждых трех из этих точек А, B, и C с d(AC) больше или равно каждому из d(AB) и d(до н.э), неравенство треугольника d(AC) ≤ d(AB) + d(до н.э) выполняется с равенством.

Теория чисел

Параллелизм (плоский двойной)

График коллинеарности

Учитывая частичная геометрия п, где две точки определяют не более одной линии, a график коллинеарности из п это график чьи вершины являются точками п, где две вершины соседний тогда и только тогда, когда они определяют строку в п.

Использование в статистике и эконометрике

Это означает, что если различные наблюдения (Икс_1я, Икс_2я ) нанесены в (Икс₁, Икс₂) плоскости эти точки коллинеарны в смысле, определенном ранее в этой статье.

Идеально мультиколлинеарность относится к ситуации, в которой k (k ≥ 2) объясняющие переменные в множественная регрессия модели идеально линейно связаны, согласно

для всех наблюдений я. На практике мы редко сталкиваемся с идеальной мультиколлинеарностью в наборе данных. Чаще проблема мультиколлинеарности возникает, когда существует «сильная линейная связь» между двумя или более независимыми переменными, что означает, что

Концепция чего-либо боковая коллинеарность расширяет эту традиционную точку зрения и указывает на коллинеарность между объясняющими и критериальными (т. е. объясненными) переменными. [10]

Источник

Векторы: третий уровень сложности

Знакомимся с коллинеарностью.

Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.

Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:

Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.

Что за коллинеарность

Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.

И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.

Коллинеарные векторы Неколлинеарные векторы

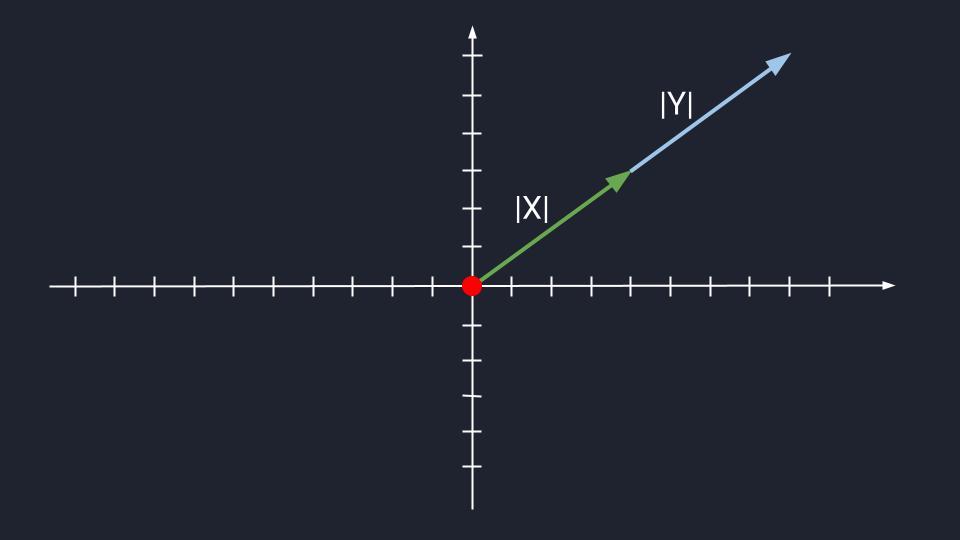
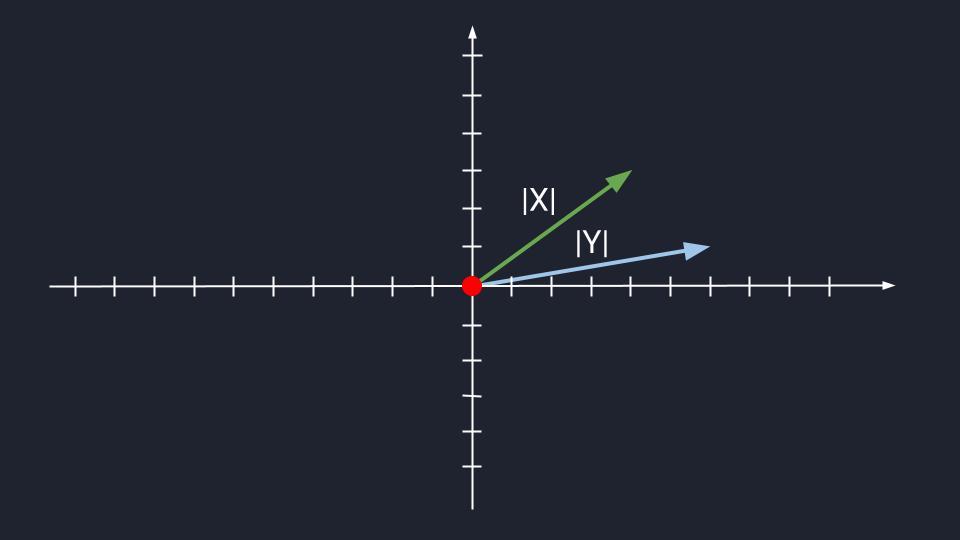
Сложение коллинеарных и неколлинеарных векторов

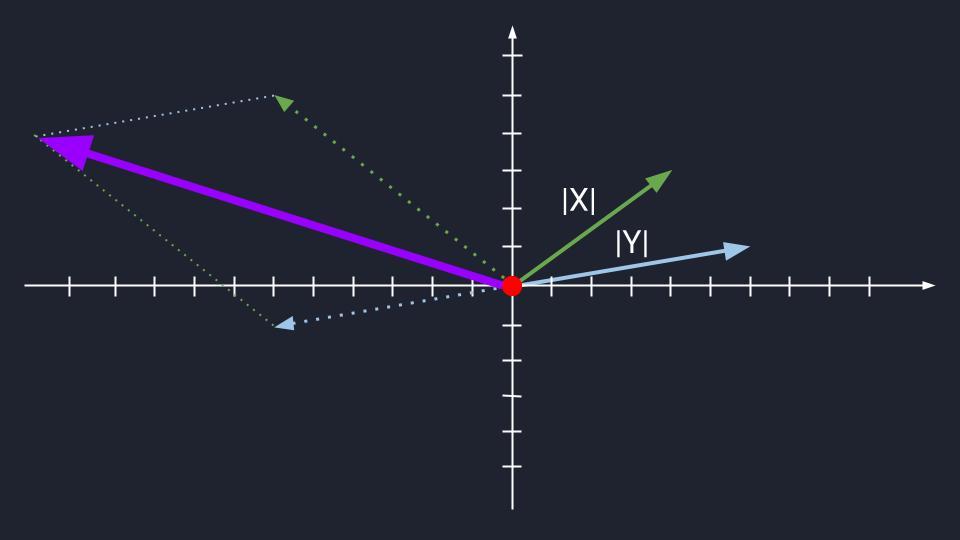
Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.

Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.

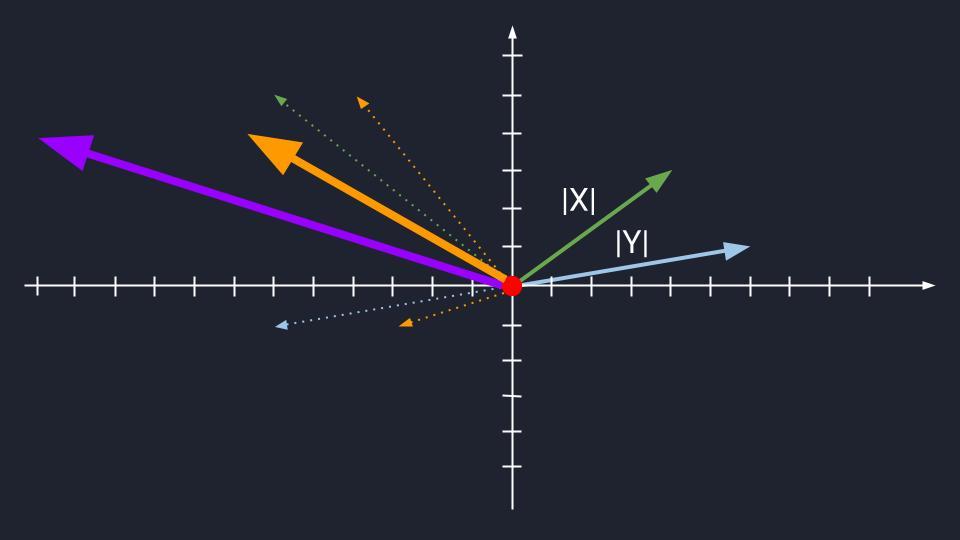
Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.

Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.

У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.

Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.

Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.

Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый вектор

Как определять неколлинеарность

Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.

А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,

Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.

Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:

По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.

Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.

👉 Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».

Составляем систему уравнений:

Вычисляем значение λ:

Сравниваем результат и делаем вывод:

Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.

Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.

Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.

Получаем такую пропорцию:

Считаем значение и сравниваем результат:

Равенство не выполняется, и поэтому между векторами нет зависимости.

Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.

Записываем в две строки координаты наших векторов:

Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:

В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.

Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.

И наоборот: нулевой определитель указывает на линейную зависимость векторов.

Что из этого нужно запомнить

Что дальше

Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.

Источник