Что означает команда 2 q2 для машины тьюринга

Машина Тьюринга

В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.
Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.

Что собой представляет машина Тьюринга?

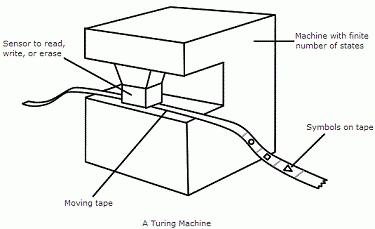
Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой.
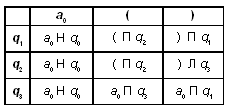
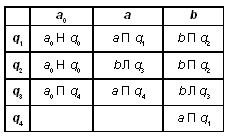
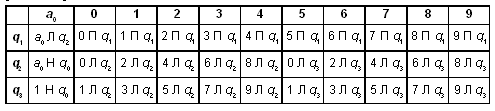
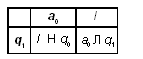
Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:

Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).

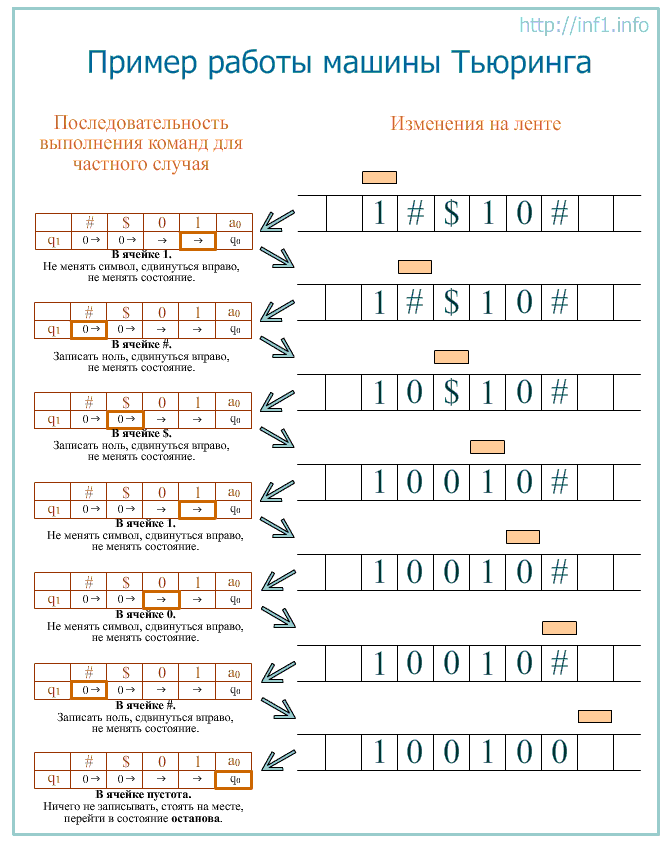
Пример работы машины Тьюринга

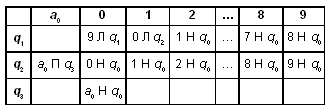
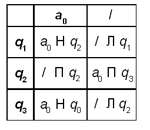
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):

Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние q₂ (команды которого совпадают с командами q₁ предыдущей программы).

Источник

Навигация

Календарь

Машина Тьюринга. Задачи и решения

Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.

Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.

Рассмотрим работу Машины Тьюринга.

Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.

Таким образом Машина Тьюринга формально описывается набором двух алфавитов:

A= — внешний алфавит, служит для записи исходных данных

Q= — внутренний алфавит, описывает набор состояний считывающе-печатного устройства.

Каждая ячейка ленты может содержать символ из внешнего алфавита A = (В нашем случае A=<0, 1>)

Допустимые действия Машины Тьюринга таковы:

1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)

2) сместиться в соседнюю ячейку

3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q

Машина Тьюринга — это автомат, который управляется таблицей.

Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = . В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.

В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «

Источник

Что означает команда 2 q2 для машины тьюринга

Абстрактные вычислительные машины

Материал взят с ресурса Планета информатики

То есть, всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.

Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой. Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:

Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).

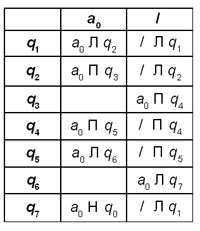
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):

Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние Q2 (команды которого совпадают с командами Q1 предыдущей программы).

Материал взят с ресурса Планета информатики

Решение этой задачи аналогично рассмотренному выше примеру.

Задача 4 (усложнение задачи 3)

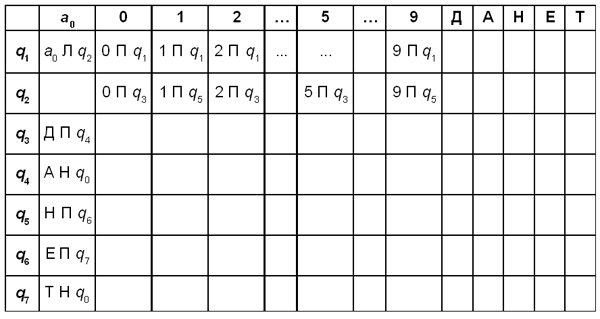
Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.

Решение этой задачи обычно вызывает у школьников затруднение. При разборе решения этой задачи можно пойти, например, следующим путем.

Рассмотрите со школьниками следующие варианты входных слов и попросите их сформулировать, что должна делать машина Тьюринга, каков внешний вид выходного слова, чем с точки зрения машины Тьюринга эти варианты различаются:

Рассмотрим следующие варианты входных слов:

Однако, как ни странно, решение этой задачи вызывает большие трудности. Очень часто ученики строят машину Тьюринга, которая выполняет циклические действия: последовательно пододвигают правые n штрихов к левым.

В этом случае их программа выглядит следующим образом:

На примере этой задачи четко видно, как часто дети пытаются решить задачу уже знакомыми способами. Мне кажется, что, предлагая ученикам задачи на составление машин Тьюринга, мы развиваем способность к нахождению необычных решений, развиваем способность творчески думать!

Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи.

Идея решения (условие останова). На ленте есть два исходных массива штрихов.

Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.

При решении этой задачи следует обратить внимание на правильное выписывание алфавита:

Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и её начальное состояние (то есть состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из пронумерованных не обязательно упорядоченных строк команд, если в каждой команде указана строка, на которую нужно перейти. Обычно принимается, что если в команде переход не указан, то переход происходит на следующую строку. Каждая команда имеет следующий синтаксис:

После программы запуска возможны варианты:

Источник

Машина Тьюринга

Содержание

Машина Тьюринга (англ. Turing machine) — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга.

Неформально машина Тьюринга определяется как устройство, состоящее из двух частей:

При запуске машины Тьюринга на ленте написано входное слово, причём на первом символе этого слова находится головка, а слева и справа от него записаны пустые символы. Каждый шаг головка может перезаписать символ под лентой и сместиться на одну ячейку, если автомат приходит в допускающее или отвергающее состояние, то работа машины Тьюринга завершается.

Определение [ править ]

Определение машины [ править ]

Отметим, что существуют различные вариации данного выше определения (например, без отвергающего состояния или с множеством допускающих состояний), которые не влияют на вычислительные способности машины Тьюринга.

Определение процесса работы [ править ]

Особо следует рассмотреть случай переходов по пробельному символу:

Для машины Тьюринга, которая пишет символ [math]B[/math] на ленту также можно дать аналогичное формальное определение. Оно будет отличаться тем, что символы в строчках конфигурации могут содержать пробелы, и для того, чтобы эти строчки имекли конечную длину, нужно аккуратно учесть наличие пробелов при записи правил перехода.

Результат работы [ править ]

Примеры машин-распознавателей и машин-преобразователей будут даны ниже.

Примеры машин Тьюринга [ править ]

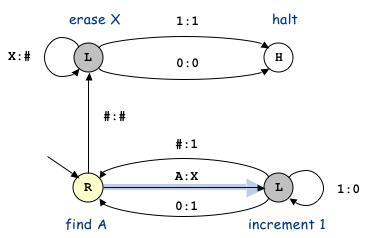
Прибавление единицы [ править ]

Для начала приведём пример машины-преобразователя, которая прибавляет единицу к числу, записанному на ленте в двоичной записи от младшего бита к старшему. Алгоритм следующий:

Проверка того, является ли слово палиндромом [ править ]

Варианты машины Тьюринга [ править ]

В этом разделе приведены различные варианты машин Тьюринга, которые не отличаются от обычных машин Тьюринга по вычислительной мощности.

Многодорожечная машина Тьюринга [ править ]

Машина Тьюринга с полубесконечной лентой [ править ]

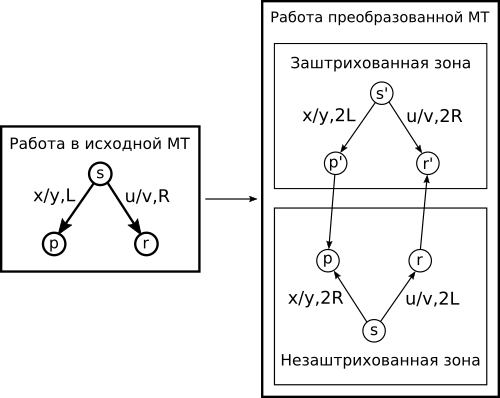
Заменив у машины Тьюринга бесконечную в обе стороны ленту на бесконечную в одну сторону, мы не теряем в вычислительной мощности. По произвольной машине Тьюринга строится двухдорожечная машина с полубесконечной лентой.

Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с бесконечной лентой следующим образом:

Затем перенумеруем ячейки, и запишем символ [math]c \in \Pi \setminus \Sigma, B[/math] в начало ленты, который будет означать границу рабочей зоны:

Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации.[math]\triangleleft[/math]

Многоленточная машина Тьюринга [ править ]

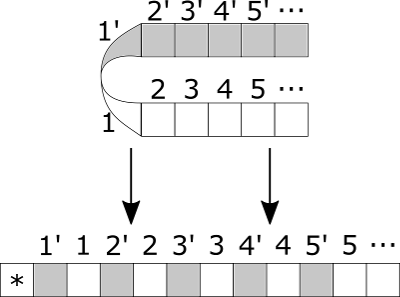
Многоленточная машина с [math]n[/math] дорожками эмулируется многодорожечной машиной с [math]2n[/math] дорожками следующим образом: каждая нечётная дорожка соответствует ленте исходной машины, а на каждой чётной дорожке отмечены специальным символом [math]*[/math] позиция головки на ленте выше (считаем, что ленты нумеруются сверху вниз).

Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов [math]*[/math] символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага.

Аланом Тьюрингом было сформулировано следующее утверждение:

Иными словами, тезис говорит о том, что любой алгоритм можно запрограммировать на машине Тьюринга.

Универсальная машина Тьюринга [ править ]

Существует машина Тьюринга, которая принимает на вход закодированное описание произвольной машины и входную строку и эмулирует работу закодированной машины на заданном входном слове. Иными словами, универсальный язык перечислим с помощью машины Тьюринга. Ссылки на явные конструкции универсальных машин Тьюринга приведены ниже.

Источник

Реализация алгоритма в машине Тьюринга

На ряде примеров покажем, как строятся тьюринго-вы машины, реализующие некоторые простые арифме­тические алгоритмы.

Пример 1.Реализация в машине Тьюринга алгорит­ма перехода от n к n+1 в десятичной системе счисления.

Пусть дана десятичная запись натурального числа п и требуется указать десятичную запись числаn+1, т.е. вычислить функциюf(n) = п + 1.

Ясно, что здесь внешний алфавит машины должен содержать все цифры О, 1, 2, 3, 4, 5, 6, 7, 8, 9 исимвол пустой клеткиa_Q. Числоп будем записывать в десятич­ной системе на ленте, причем цифры будут помещаться по одной в каждой клетке подряд без пропусков.

Чтобы решить поставленную задачу, машина долж­на в первом такте работы стереть последнюю цифру чис­ла л, заменить ее цифрой на единицу большей и перейти в стоп-состояние, если последняя цифра была меньше цифры 9.

Бели же последняя цифра числа n была 9, то машина должна, стерев цифру 9, записать в освободившуюся клет­ку цифру 0 и произвести сдвиг влево к соседнему более высокому разряду, оставаясь в том же начальном состоя­нии. Здесь во втором такте работы машина должна при­бавить единицу к цифре более высокого разряда.

Очевидно, что в случае сдвига влево, управлявшая го­ловка машины может выйти на пустую клетку в случае, когда цифры более высокого разряда нет. При этом ма­шина вписывает в пустую клетку цифру 1.

Из сказанного следует, что при реализации алгорит­ма вычисления функцииf(n) = n + 1машина может пре­бывать лишь в двух состоянияхq_l иq₀.

Таким образом, машина Тьюринга, реализующая алгоритм перехода от n кn+1 в десятичной системе счис­ления будет иметь вид:

На рис. 4 и 5 выписаны соответствующие конфигурации для n = 183 и n = 399:

Пример 2. Алгоритм сложения натуральных чисел» Пусть на ленту подается два числа, заданных набо­рами палочек; например, 2 и 3. Нужно сложить эти числа.

Будем обозначать символ сложения звездочкой. Та­ким образом, на ленте машины будет записано слово

А0 (1) Требуется предложить функциональную схему, которая, будучи примененной, к слову (1), давала бы в ре­зультате сумму чисел 2 и 3, то есть слово а0

А0 (2) Опишем процесс работы машины для решения зада­чи. Пусть в начальный момент обозревается самая левая палочка. Ее нужно сдвинуть вправо, минуя все палочки и звездочку до тех пор, пока не будет достигнута первая пустая клетка. В эту пустую клетку вписывается первая палочка. Затем нужно вернуться за второй палочкой и ее перенести вправо так же, как это делалось с первой палочкой. После этой процедуры нужно вернуться к звез­дочке, стереть ее и остановиться. Изобразим все такты работы машины в виде соответствующих конфигураций: 1. a0 ||*

Машина тьюринга сложение двух чисел

»Я не знаю, кто я — Тьюринг, которому снится, что он машина,
или машина, которой снится, что она Тьюринг!».
Дао Программирования

Для более близкого знакомства с машиной Тьюринга, рекомендую её имитатор Algo2000 Зартидова Радика. На мой взгляд — это лучшая реализация имитатора машины Тьюринга.

Машина тьюринга сложение двух чисел

6.
Составьте программы для машины Тьюринга, которые выполняют
сложение и вычитание двух чисел в десятичной системе счисления.

ответ

Если при стирании ведущего нуля автомат «попадает» на минус — можно остановить. На ленте останется результат вычетания большего числа из меньшего (отрицательный результат).
Т.е. в ячейке в ряду «-» и колонке «О5» изменить команду: оставить «-«, остаться на месте, останов.

Условие — машина Тьюринга
Число представлено в двоичном формате в различных конечных автоматах, например, 5 представлено как (101), но в случае добавления с использованием машины Тьюринга используется унарный формат. В унарном формате число представлено либо всеми единицами, либо всеми нулями. Например, 5 будет представлен последовательностью из пяти нулей или пяти единиц. 5 = 1 1 1 1 1 или 0 0 0 0 0. Позволяет использовать нули для представления.

Для добавления 2 чисел с использованием машины Тьюринга оба эти числа приводятся в качестве входных данных для машины Тьюринга, разделенных «с».

Примеры — (2 + 3) будут заданы как 0 0 c 0 0 0:

Подход используется —
Преобразуйте 0 в первом числе в X, а затем пройдитесь по всему вводу и преобразуйте первый пробел в 0. Затем двигайтесь влево, игнорируя все 0 и «c». Пройдите позицию рядом с X, а затем повторяйте ту же процедуру до тех пор, пока мы не получим «c» вместо X при возврате. Преобразовать c в пустую и сложение завершено.

Шаг 1: конвертируйте 0 в X и переходите к шагу 2. Если символ «с», то конвертируйте его в пробел (B), двигайтесь вправо и переходите к шагу 6.

Шаг 2: Продолжайте игнорировать 0 и двигайтесь вправо. Не обращайте внимания на «c», двигайтесь вправо и переходите к шагу 3.

Шаг 3: продолжайте игнорировать 0 и двигайтесь вправо. Преобразуйте пробел (B) в 0, переместитесь влево и перейдите к шагу 4.

Шаг 4: продолжайте игнорировать 0 и двигайтесь влево. Не обращайте внимания на «c», двигайтесь влево и переходите к шагу 3.

Шаг 5: продолжайте игнорировать 0 и двигайтесь влево. Не обращайте внимания на X, двигайтесь влево и переходите к шагу 1.

Главная > Документ

Машина Тьюринга – математическая модель процессов преобразования информации, с ее помощью можно реализовать любой алгоритм.

Эту модель можно представить как устройство, состоящее из следующих частей:

бесконечной или полу бесконечной ленты, разделенной на ячейки,

читающе — записывающей головки,

управляющего устройства, которое за один такт работы машины а) считывает из ячейки символ, б) записывает в него новый (может быть тот же) символ, в) перемещается влево, вправо или остается на месте, г) изменяет состояние.

При составлении алгоритмов на машине Тьюринга обычно используют следующие приемы: 1) машина запоминает тот или иной символ, переходя в различные состояния, 2) отметка просмотренного символа делается с помощью символов внешнего (дополнительного) алфавита.

Будем считать, что рассматриваемые выражения и строки отделяются на ленте слева и справа пробелами и лента бесконечная в оба конца.

Алгоритмы удобно записывать в виде таблицы, где заголовками столбцов являются символы допустимого алфавита, а заголовками строк – состояния машины. В ячейках стоят конфигурации машины, соответствующие определенным символам и состояниям.

Машина Тьюринга: описание и примеры машин Тьюринга

Машина Тьюринга — одно из самых интригующих и захватывающих интеллектуальных открытий 20-го века. Это простая и полезная абстрактная модель вычислений (компьютерных и цифровых), которая является достаточно общей для воплощения любой компьютерной задачи. Благодаря простому описанию и проведению математического анализа она образует фундамент теоретической информатики. Это исследование привело к более глубокому познанию цифровых компьютеров и исчислений, включая понимание того, что существуют некоторые вычислительные проблемы, не решаемые на общих пользовательских ЭВМ.

Что это и кто создал

Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.

Машина Тьюринга является вычислительным устройством, состоящим из головки чтения/записи (или «сканера») с бумажной лентой, проходящей через него. Лента разделена на квадраты, каждый из которых несет одиночный символ — «0» или «1». Назначение механизма состоит в том, что он выступает и как средство для входа и выхода, и как рабочая память для хранения результатов промежуточных этапов вычислений.

Из чего состоит устройство

Каждая такая машина состоит из двух составляющих:

Как работает механизм

Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.

Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.

Свойства механизма

Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:

Функции машины Тьюринга

Программа для устройства

Программы для механизма Тьюринга оформляются таблицами, в которых первые строка и столбец содержат символы внешнего алфавита и значения возможных внутренних состояний автомата — внутренний алфавит. Табличные данные являются командами, которые воспринимает машина Тьюринга. Решение задач происходит таким образом: буква, считываемая головкой в ячейке, над которой она в данный момент находится, и внутреннее состояние головки автомата обусловливают, какую из команд необходимо выполнять. Конкретно такая команда находится на пересечении символов внешнего алфавита и внутреннего, находящихся в таблице.

Составляющие для вычислений

Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.

Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.

Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.

Алгоритм для автомата

Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:

Таким образом, при написании программ для каждой пары символов либо положений необходимо точно описать три параметра: a_i – элемент из выбранного алфавита A, направление сдвига каретки («←” влево, «→” вправо, «точка” — отсутствие перемещения) и q_k — новое состояние устройства. К примеру, команда 1 «←” q₂ имеет значение «заместить символ на 1, сдвинуть головку каретки влево на один шаг-ячейку и сделать переход в состояние q₂”.

Машина Тьюринга: примеры

Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.

Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:

Здесь q₁ — состояние изменения цифры, q₀ — остановка. Если в q₁ автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q₀, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q₁. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q₀ – остановка.

Состояние q₁: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q₂; если определен “a₀”, то остановка.

Состояние q₂: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q₃.

Состояние q₃: осуществить удаление сначала символа “(”, а затем “)” и перейти в q₁.

Элементарная Машина Тьюринга

Введение

Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.[1]

Описание формальной модели алгоритма на основе рекурсивных функций

Определение понятия примитивно рекурсивной функции является индуктивным. Оно состоит из указания класса базовых примитивно рекурсивных функций и двух операторов (подстановки и примитивной рекурсии), позволяющих строить новые примитивно рекурсивные функции на основе уже имеющихся.

К базовым примитивно рекурсивным фунциям относят:

Задание: доказать примитивную рекурсивность функции «ближайшее к n простое число».

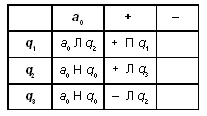
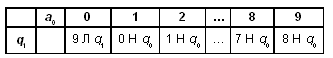
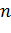Протестируем приведённую выше схему вычисления ближайшего к простого числа на конкретных примерах.

В качестве параметра возьмём простое число 5.

Рисунок 1.1 — Тест алгоритма на числе 5

В качестве параметра возьмём 15:

Рисунок 1.2 — Тест алгоритма на числе 15

Аналитическая модель Машины Тьюринга

Элементарная Машина Тьюринга

Задание: реализовать Машину Тьюринга для вычисления функции получения остатка от деления двух чисел в унарном коде с сохранением данных. Описать полученную машину тремя способами: правилами переходов, таблицей состояний и графом состояний.

Во входных данных находятся делимое и делитель в унарном коде, разделённые символом «*». В выходных данных к входным должна добавиться конструкция «= », где — результат вычислений в унарном коде.

Пример входных данных: 11111111*111

Пример выходных данных: 11111111*111=11

Ниже приведено описание элементарной машины Тьюринга тремя способами: списком правил переходов, таблицей состояний и графом:

2.1.6 Описание Машины Тьюринга таблицей состояний

Таблица 2.1 — Таблица состояний Машины Тьюринга

Продолжение таблицы 2.1

Рисунок с графом переходов.

Рисунок 2.2 — Граф переходов

На рисунке 2.3 приведено тестирование работы Машины Тьюринга для входных данных 11111*11.

2.2 Композиция Машин Тьюринга

Построить композицию Машин Тьюринга для вычисления ближайшего к s простого числа в унарном коде без сохранения исходных данных.

Пример входных данных: 111111

Пример выходных данных: 11111

Ниже привдена блок-схема алгоритма, реализующего вычисление заданного алгоритма:

Рисунок 2.4 — Блок схема алгоритма поиска ближайшего к s простого числа

В композиции будут участвовать следующие Машины Тьюринга:

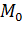— – машина копирования;

— – машина проверки на простоту;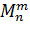

— – машина выбора m-го элемента из n;

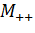— — машина увеличения на единицу;

— машина уменьшения на единицу.

Теперь распишем машину , которая используется для проверки числа на простоту.

В композиции будут участвовать машины:

— – машина копирования;

— – машина выбора m-го элемента из n;

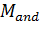— — машина логическое и;

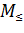— — машина сравненения;

— — машина установки двойки;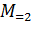

— — машина проверки на равенство двойке;

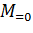— — машина проверки на равенство нулю;

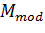— — машина вычисления остатка от деления;

— — машина увеличения на единицу;

— — машина уменьшения на единицу;

— — машина сложения.

СХЕМА КОМПОЗИЦИИ ИЗ 3 ЛАБЫ

Рисунок 2.6 — Композиция машины проверки на простоту

Источник