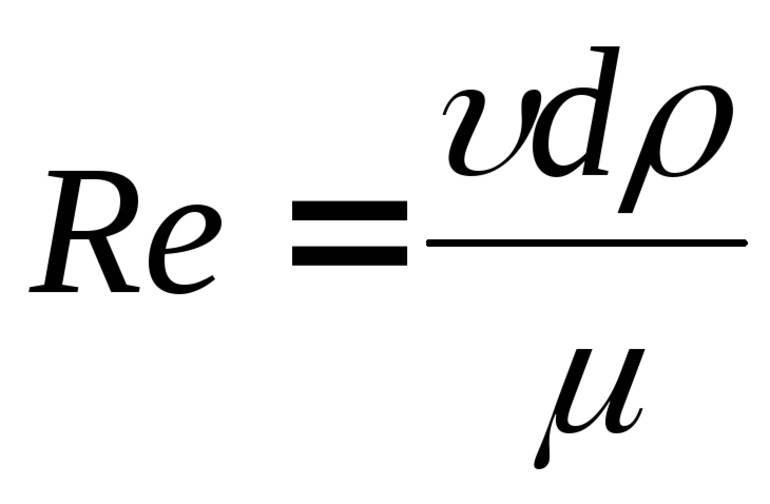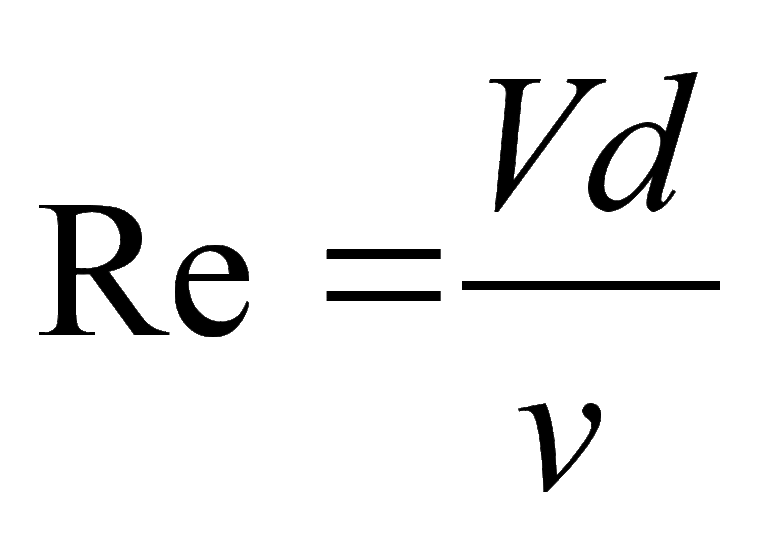Что означает критическое число рейнольдса
Число Рейнольдса (Re) — формула определения и критические значения
Осборн Рейнольдс (1842—1912) — ирландский учёный и инженер, работавший в области гидромеханики и гидравлики, основные труды которого были связаны с теориями динамического течения вязкой жидкости и турбулентности. Во время экспериментов он получил безразмерную величину, характеризующую поток жидкости или воздуха, названную впоследствии числом Рейнольдса.
Опыты Рейнольдса
Рейнольдс проводил эксперименты на установке, представлявшей собой бак с водой, к которому в нижней части была присоединена выходная стеклянная трубка с краном на конце. Бак постоянно наполнялся водой, а расход воды мерился при помощи мерного бачка и секундомера. Над баком находился сосуд с краской, которая попадала в воду по тонкой трубочке с краном.
Рейнольдс доказал, что при значении числа Re 2000—3000 поток становится турбулентным, а при Re меньше нескольких сотен — поток полностью ламинарный.
Режимы течения жидкости
Опыты, проводившиеся Рейнольдсом, подтвердили наличие двух режимов течения жидкости — турбулентного и ламинарного. Учёный сформулировал общие условия существования режимов и переходного состояния между ними. Разные жидкости при протекании по трубам, обтекании преград или растекании по поверхности демонстрируют различные свойства. Густая липкая жидкость, например, клей, обладает большей вязкостью, чем лёгкая и подвижная вода. Степень вязкости определяется коэффициентом динамической вязкости η («эта»). Для ламинарного потока свойственны следующие признаки:
Турбулентное течение — хаотический поток, каждая молекула которого двигается произвольно по непредсказуемой траектории. При этом в потоке образуются завихрения. Но, несмотря на хаотичность перемещения частиц, общий гидравлический поток имеет направление и скорость, которая оценивается по средним значениям. В большей части поперечного сечения скорость только немного меньше максимальной, но вблизи стенок она резко падает.
Рейнольдс провёл значительное количество опытов с разными жидкостями для определения числа, безразмерная величина которого описывает характер гидравлического потока. Это число имеет обозначение Re. Экспериментально было установлено, что при превышении числом Рейнольдса критической величины наблюдается переход движения жидкости, текущей в трубе, из ламинарного режима в турбулентный.
Число Рейнольдса характеризует режим движения и даёт правильные значения при расчёте для напорных потоков. В потоках без напора переходный период увеличивается, и использование Re в качестве критерия не всегда подходит. Например, в водохранилищах значения велики, но там происходит ламинарное течение.
Скорость среды
Скорость, при которой изменяется режим потока — критическая. Существует 2 вида: одна соответствует переходу от ламинарного течения к турбулентному и другая, соответствующая обратному переходу от турбулентного к ламинарному. Между этими значениями может наблюдаться как один, так и другой режим. Этот период определяется как переходный. Для случая движения жидкости в трубопроводе Рейнольдс назвал следующие параметры, от которых зависит режим гидравлического потока:
При этом лёгкость осуществления турбулентного режима прямо пропорциональна поперечному сечению трубы и плотности и обратно пропорциональна вязкости. Формула числа Рейнольдса:
Подставляя в эту формулу соответствующие параметры скорости среды, её плотности, вязкости и размеры трубы, можно произвести расчёт значения числа Re и определить режим потока. Число Re не имеет размерности. Это становится понятно, если подставить в формулу все параметры со своими единицами измерения. В результате сокращения получается безразмерное число. Для гидравлического потока в прямой круглой трубе с гладкими стенками критическое значение Re в норме равно 2100—2300. Анализ показывает, что критическое значение числа Re возрастает в сужающихся трубопроводах и снижается в расширяющихся.
При расчётах обычно принимают только одно критическое значение числа Re. Предполагается, что Re 2300 — турбулентному. Течение жидкости в переходной зоне не рассматривается. Это обеспечивает некоторый запас и увеличивает надёжность расчётов. Для газов Re критическое достигается при значительно больших скоростях течения, чем у жидкостей, так как у них намного больше кинематическая вязкость (ν = η / ρ).
Турбулентное движение наблюдается чаще, чем ламинарное. Скорости при хаотичном движении более равномерно распределены по сечению потока. Это происходит в связи с перемешиванием молекул с разными скоростями и уравниванием средней скорости по всему поперечному сечению. Ламинарные потоки наблюдается при движении вязких жидкостей по трубам, в течении грунтовых вод и крови в живых организмах.
Значение числа Re
Жидкость в гидравлическом потоке имеет инерцию и пытается поддерживать имеющуюся скорость. При большой вязкости среды внутреннее трение между слоями оказывает значительное сопротивление. Число Re зависит от соотношения между силами инерции и трения. Большие значения Re соответствуют случаю, когда сопротивление трения мало и не может загасить турбулентность. Малые величины Re относятся к обстоятельствам, когда трение уменьшает турбулентность и превращает гидравлический поток в ламинарный.
Физический смысл числа Рейнольдса — отношение сил инерции потока к силам вязкости. Можно говорить, что это соотношение выражает зависимость между кинетической энергией потока и тепловыми потерями энергии на трение при аналогичной длине.
Число Рейнольдса используется при моделировании потоков в различных газах и жидкостях, так как режим течения зависит только от соотношения физических величин: плотности, вязкости, скорости и размеров элемента, которое выражается числом Re, поэтому можно использовать для эксперимента в аэродинамической трубе уменьшенный прототип летательного аппарата и выбрать скорость потока воздуха так, чтобы число Рейнольдса соответствовало реальному для аппарата в полёте. Сейчас нет необходимости в использовании аэродинамической трубы. Все воздушные потоки можно моделировать с помощью компьютера.
Рейнольдс внёс большой вклад в гидравлику, гидродинамику и механику. Он представил дифференциальные уравнения осреднённого движения жидкости, учитывающие турбулентные напряжения, создал труды по теории смазки, определил критерий подобия двух различных течений, исследовал явления кавитации на примере винтовой лопасти, модернизировал устройство центробежных насосов. В 1888 году он был награждён медалью Лондонского королевского общества.
Опыты О.Рейнольдса. Критические числа Рейнольдса. Определение числа Рейнольдса.
То, что движение жидкости может происходить по разному отмечали Хаген Г., Менделеев Д.И., но впервые экспериментальное исследование режимов течения жидкости выполнил английский физик О.Рейнольдс, в 1883г.
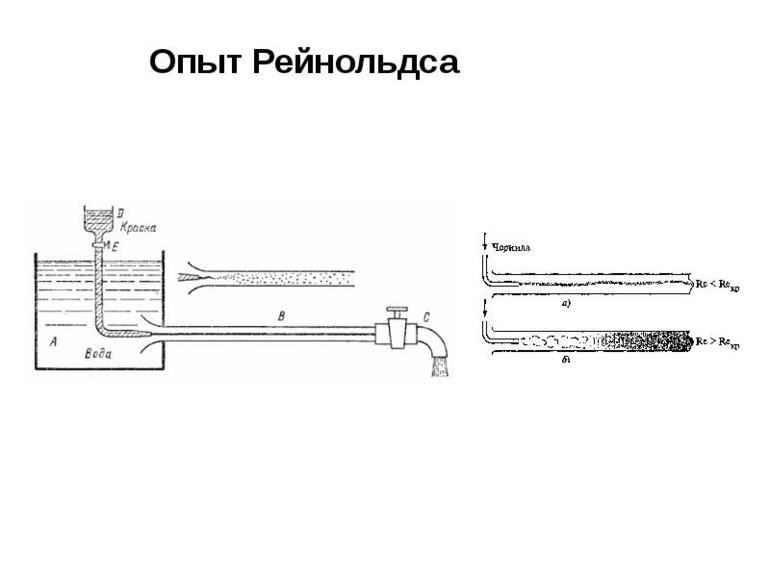
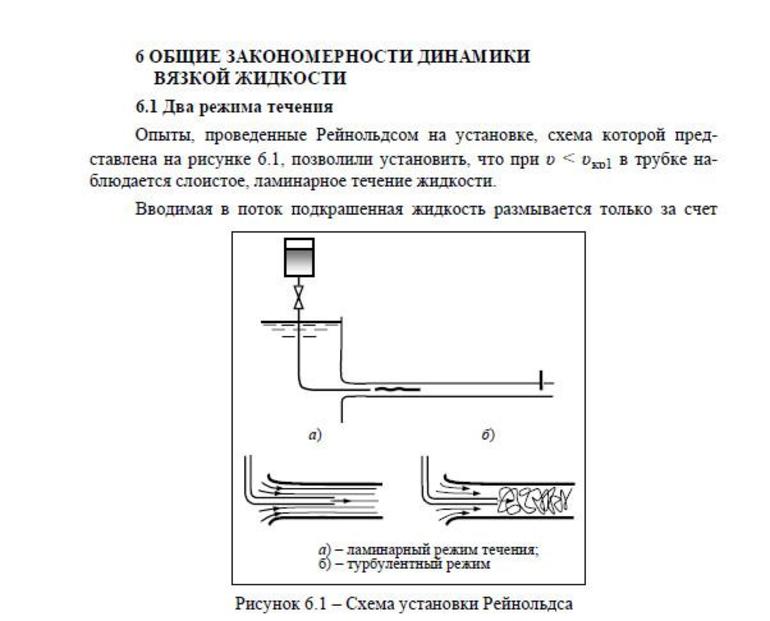
Рейнольдс проводил опыты на такой установке (рис.6.1.)
Установка состоит из бака 1 с исследуемой жидкостью и стеклянной горизонтальной трубы 2 с краном 3 для регулирования расхода. Для измерения расхода имеется мерная емкость 4. Над баком 1 имеется небольшая емкость 5 с подкрашенной жидкостью, которая может поступать через краник 6 по тоненькой трубочке 7 на вход трубы 2.
Опыты проводились следующим образом. Открывались краны 3 и 6, измерялся расход жидкости и одновременно проводились наблюдения за струйкой окрашенной жидкости в прозрачной трубе 2. При малых скоростях движения в трубе 2 окрашенная струйка не расплывается и имеет вид натянутой линии, т.е. течение имеет слоистый характер и отсутствует перемешивание жидкости. Такой режим течения получил название ламинарным.
При увеличении скорости течения в трубке 2 струйка краски начинает колебаться, затем размываться и перемешиваться, причем становится заметным вихреобразования и вращательное движение жидкости. Такой режим течения называется турбулентным. Движение отдельных частиц жидкости при таком режиме оказывается хаотичным, появляются нормальные к направлению течения составляющие скорости.
Существует еще некоторый переходной режим течения, при котором струйка краски еще не размывается полностью, но и не имеет вид прямолинейной.
Рейнольдс установил общие условия, при которых возможно существование ламинарного и турбулентного режимов движения жидкости и переход от одного к другому. Оказалось, что режим течения жидкости в трубе зависит от безразмерного числа, которое учитывает среднюю скорость U, диаметр трубы d, плотность жидкости Б и ее вязкость ј. Это число, которое получило название число Re, имеет вид:
Re = UdБ / ј = Ud / Ѕ
Таким образом, зная скорость движения жидкости, ее вязкость и диаметр трубы можно расчетным путем найти число Re и определить режим течения жидкости.
Режим течения характеризуется числом Re.
Для каждого вида течения существует такое критическое число РейнольдсаReкр, что если характеризующее поток число Re Reкр течение обычно турбулентное.
Число Рейнольдса определяется следующим соотношением:
· 
— плотность среды, кг/м 3 ;
· 
— характерная скорость, м/с;
· 
— гидравлический диаметр, м;
· 
— динамическая вязкость среды, Н·с/м 2 ;
· 
— кинематическая вязкость среды, м 2 /с ( 
);
· 
— объёмная скорость потока;
· 
— площадь сечения трубы.
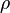
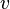
Для каждого вида течения существует критическое число Рейнольдса, 
, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При 
течение происходит в ламинарном режиме, при 
возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, такими как изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой [источник не указан 1045 дней] трубе с очень гладкими стенками 
. Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке 
.
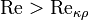
Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается — то есть, неустойчивая турбулентность. Числу Reкр 2300 соответствует интервал 2300-10 000; для упомянутого примера с тонкими плёнками это 20-120 — 1600.
Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение. Напротив, возмущения потока могут значительно снижать величину .
Теперь давайте обратимся к потоку жидкости. Различные жидкости при течении в трубах, растекании по поверхности или обтекании препятствий обладают различными свойствами. Густая, клейкая жидкость (например, мед) обладает, как говорят физики, большей вязкостью, нежели легкая и подвижная жидкость (например, бензин). Степень вязкости жидкости определяется так называемым коэффициентом вязкости, который принято обозначать греческой буквой η («эта»). У густых, клейких жидкостей коэффициент вязкости η в десятки и сотни раз выше, чем у легких и текучих.
Рейнольдсу удалось обнаружить безразмерное число, описывающее характер потока вязкой жидкости. Сам ученый получил его экспериментально, проведя изнурительную серию опытов с различными жидкостями, однако вскоре было показано, что его можно вывести и теоретически из законов механики Ньютона и уравнений классической гидродинамики. Это число, которое теперь называют числом Рейнольдса и обозначают Re, характеризует поток и равно:
где ρ — плотность жидкости, v — скорость потока, а L — характерная длина элемента потока (в этой формуле важно помнить, что Re — это одно число, а не произведение R × e).
Теперь давайте посмотрим на размерность составляющих числа Рейнольдса:
Отсюда получаем, что размерность числа Рейнольдса равна:
или, после упрощения,
Итак, все единицы измерения в размерности числа Рейнольдса сокращаются, и оно действительно оказывается безразмерной величиной.
Рейнольдсу удалось выяснить, что при значении этого числа 2000–3000 поток становится полностью турбулентным, а при значении Re меньше нескольких сотен — поток полностьюламинарный (то есть не содержит завихрений). Между двумя этими значениями поток носит промежуточный характер.
Можно, конечно, считать число Рейнольдса чисто экспериментальным результатом, однако его можно интерпретировать и с позиции законов Ньютона. Жидкость в потоке обладает импульсом, или, как иногда говорят теоретики, «инерционной силой». По сути, это означает, что движущаяся жидкость стремится продолжить свое движение с прежней скоростью. В вязкой жидкости этому препятствуют силы внутреннего трения между слоями жидкости, стремящиеся затормозить поток. Число Рейнольдса как раз и отражает соотношение между двумя этими силами — инерции и вязкости. Высокие значения числа Рейнольдса описывают ситуацию, когда силы вязкости относительно малы и не способны сгладить турбулентные завихрения потока. Малые значения числа Рейнольдса соответствуют ситуации, когда силы вязкости гасят турбулентность, делая поток ламинарным.
Число Рейнольдса очень полезно с точки зрения моделирования потоков в различных жидкостях и газах, поскольку их поведение зависит не от реальной вязкости, плотности, скорости и линейных размеров элемента потока, а лишь от их соотношения, выражаемого числом Рейнольдса. Благодаря этому можно, например, поместить в аэродинамическую трубу уменьшенную модель самолета и подобрать скорость потока таким образом, чтобы число Рейнольдса соответствовало реальной ситуации полномасштабного самолета в полете. (Сегодня, с развитием мощной компьютерной техники, нужда в аэродинамических трубах отпала, поскольку воздушные потоки можно смоделировать на компьютере. В частности, первым гражданским авиалайнером, полностью спроектированным исключительно с использованием компьютерного моделирования, стал «Боинг-747». В этой связи любопытно отметить, что при проектировании гоночных яхт и высотных зданий до сих пор практикуется их «обкатка» в аэродинамических трубах.)
Число Рейнольдса
Движение жидкости, несмотря на кажущуюся на первый взгляд, беспорядочность движения имеет определенные закономерности. Рейнольдс в своих опытах нашел определенные общие условия, при которых возможно существование того или иного режима течения и переход от одного режима к другому.
При проведении опытов Рейнольдс в 1883г. подтвердил существование двух режимов течения жидкости. Ему удалось вычислить безразмерное число, описывающее характер потока вязкой жидкости
Содержание статьи
Опыты Рейнольдса
Опыты проводились на специальном лабораторном стенде, который представлял собой заполненный водой бак Б к которому в нижней части присоединена стеклянная трубка Т. На конце трубки установлен кран К для регулирования расхода жидкости. Расход измеряется с помощью секундомера и мерного бочка М. Бак Б постоянно заполняется водой. Над баком Б расположена ёмкость с краской С. По тонкой трубочке Т1 краска попадает в жидкость, движущуюся в трубке Т. Подачу краски регулирует кран Р.
Опыт №1. Немного приоткрываем кран К. При этом в трубке Т начинается движение жидкости. Открываем кран Р и добавляем в жидкость краску. При небольшой скорости движения в трубке Т краска становится прямолинейной и резко выделяющейся в потоке воды цветной струйкой. Эта струйка не перемешивается с остальной жидкостью. Если ввести в жидкость краску несколькими струйками, то они так и будут двигаться не перемешиваясь с остальной водой.
Опыт №2 При намного большем открытии крана струйка краски начинает искривляться и становится волнообразной. Открывая кран ещё больше и увеличивая скорость потока мы увидим, что струйка краски распадается на отдельные вихри и перемешивается с остальной массой воды
Вывод формулы
Рейнольдс установил, что основными факторами, определяющими характер режима являются:
средняя скорость движения жидкости υ,
диаметр трубопровода d,
плотность жидкости ρ,
абсолютная вязкость жидкости μ
При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше её вязкость, тем легче при увеличении скорости осуществить турбулентный режим.
Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр Re, учитывающий влияние перечисленных выше факторов, называемый число Рейнольдса. Таким образом формула
Число Рейнольдса и режимы течения.
Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса:
нижнее критическое числом Рейнольдса Reкр. н.
верхнее критическое числом Рейнольдса Reкр. в.
Значение скорости, соответствующее этим значениям Re называют критическими.
При значениях числа Рейнольдса Re Reкр. в. – только турбулентный. При Reкр. н. 2300 – всегда турбулентный режимы.
При этом движении жидкости в неустойчивой зоне исключается из особого рассмотрения, это приводит к некоторому запасу и большей надежности в гидравлических расчетах в случае, если в этой зоне действительно имеет место ламинарный режим.
Без особого труда можно получить значения для Reкр для любой формы сечения, а не только круглой формы. Вспоминая, что при круглом сечении радиус
подставляем в формулу для определения числа Рейнольдса
Принимая для критического числа Рейнольдса независимо от формы живого сечения величину Reкр. = 2300, находим, что для сечения любой формы критериев для сужения о характере режима движения является величина, равная 2300 / 4 = 575.
Таким образом, режим ламинарный если значение числа Рейнольдса
И режим турбулентный, если
Видео по теме.
На практике в большинстве случаев (движение воды в трубах, каналах, реках) приходится иметь дело с турбулентным режимом. Ламинарный режим встречается реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей, что иногда имеет место в нефтепроводах, при движении жидкости в очень узких трубках и порах естественных грунтов.
Опыты Рейнольдса
Рейнольдс проводил эксперименты на установке, представлявшей собой бак с водой, к которому в нижней части была присоединена выходная стеклянная трубка с краном на конце. Бак постоянно наполнялся водой, а расход воды мерился при помощи мерного бачка и секундомера. Над баком находился сосуд с краской, которая попадала в воду по тонкой трубочке с краном.
Рейнольдс доказал, что при значении числа Re 2000—3000 поток становится турбулентным, а при Re меньше нескольких сотен — поток полностью ламинарный.
Режимы течения жидкости
Опыты, проводившиеся Рейнольдсом, подтвердили наличие двух режимов течения жидкости — турбулентного и ламинарного. Учёный сформулировал общие условия существования режимов и переходного состояния между ними. Разные жидкости при протекании по трубам, обтекании преград или растекании по поверхности демонстрируют различные свойства. Густая липкая жидкость, например, клей, обладает большей вязкостью, чем лёгкая и подвижная вода. Степень вязкости определяется коэффициентом динамической вязкости η («эта»). Для ламинарного потока свойственны следующие признаки:
Турбулентное течение — хаотический поток, каждая молекула которого двигается произвольно по непредсказуемой траектории. При этом в потоке образуются завихрения. Но, несмотря на хаотичность перемещения частиц, общий гидравлический поток имеет направление и скорость, которая оценивается по средним значениям. В большей части поперечного сечения скорость только немного меньше максимальной, но вблизи стенок она резко падает.
Рейнольдс провёл значительное количество опытов с разными жидкостями для определения числа, безразмерная величина которого описывает характер гидравлического потока. Это число имеет обозначение Re. Экспериментально было установлено, что при превышении числом Рейнольдса критической величины наблюдается переход движения жидкости, текущей в трубе, из ламинарного режима в турбулентный.
Число Рейнольдса характеризует режим движения и даёт правильные значения при расчёте для напорных потоков. В потоках без напора переходный период увеличивается, и использование Re в качестве критерия не всегда подходит. Например, в водохранилищах значения велики, но там происходит ламинарное течение.
Скорость среды
Скорость, при которой изменяется режим потока — критическая. Существует 2 вида: одна соответствует переходу от ламинарного течения к турбулентному и другая, соответствующая обратному переходу от турбулентного к ламинарному. Между этими значениями может наблюдаться как один, так и другой режим. Этот период определяется как переходный. Для случая движения жидкости в трубопроводе Рейнольдс назвал следующие параметры, от которых зависит режим гидравлического потока:
При этом лёгкость осуществления турбулентного режима прямо пропорциональна поперечному сечению трубы и плотности и обратно пропорциональна вязкости. Формула числа Рейнольдса:
Подставляя в эту формулу соответствующие параметры скорости среды, её плотности, вязкости и размеры трубы, можно произвести расчёт значения числа Re и определить режим потока. Число Re не имеет размерности. Это становится понятно, если подставить в формулу все параметры со своими единицами измерения. В результате сокращения получается безразмерное число. Для гидравлического потока в прямой круглой трубе с гладкими стенками критическое значение Re в норме равно 2100—2300. Анализ показывает, что критическое значение числа Re возрастает в сужающихся трубопроводах и снижается в расширяющихся.
При расчётах обычно принимают только одно критическое значение числа Re. Предполагается, что Re 2300 — турбулентному. Течение жидкости в переходной зоне не рассматривается. Это обеспечивает некоторый запас и увеличивает надёжность расчётов. Для газов Re критическое достигается при значительно больших скоростях течения, чем у жидкостей, так как у них намного больше кинематическая вязкость (ν = η / ρ).
Турбулентное движение наблюдается чаще, чем ламинарное. Скорости при хаотичном движении более равномерно распределены по сечению потока. Это происходит в связи с перемешиванием молекул с разными скоростями и уравниванием средней скорости по всему поперечному сечению. Ламинарные потоки наблюдается при движении вязких жидкостей по трубам, в течении грунтовых вод и крови в живых организмах.
Значение числа Re
Жидкость в гидравлическом потоке имеет инерцию и пытается поддерживать имеющуюся скорость. При большой вязкости среды внутреннее трение между слоями оказывает значительное сопротивление. Число Re зависит от соотношения между силами инерции и трения. Большие значения Re соответствуют случаю, когда сопротивление трения мало и не может загасить турбулентность. Малые величины Re относятся к обстоятельствам, когда трение уменьшает турбулентность и превращает гидравлический поток в ламинарный.
Физический смысл числа Рейнольдса — отношение сил инерции потока к силам вязкости. Можно говорить, что это соотношение выражает зависимость между кинетической энергией потока и тепловыми потерями энергии на трение при аналогичной длине.
Число Рейнольдса используется при моделировании потоков в различных газах и жидкостях, так как режим течения зависит только от соотношения физических величин: плотности, вязкости, скорости и размеров элемента, которое выражается числом Re, поэтому можно использовать для эксперимента в аэродинамической трубе уменьшенный прототип летательного аппарата и выбрать скорость потока воздуха так, чтобы число Рейнольдса соответствовало реальному для аппарата в полёте. Сейчас нет необходимости в использовании аэродинамической трубы. Все воздушные потоки можно моделировать с помощью компьютера.
Рейнольдс внёс большой вклад в гидравлику, гидродинамику и механику. Он представил дифференциальные уравнения осреднённого движения жидкости, учитывающие турбулентные напряжения, создал труды по теории смазки, определил критерий подобия двух различных течений, исследовал явления кавитации на примере винтовой лопасти, модернизировал устройство центробежных насосов. В 1888 году он был награждён медалью Лондонского королевского общества.