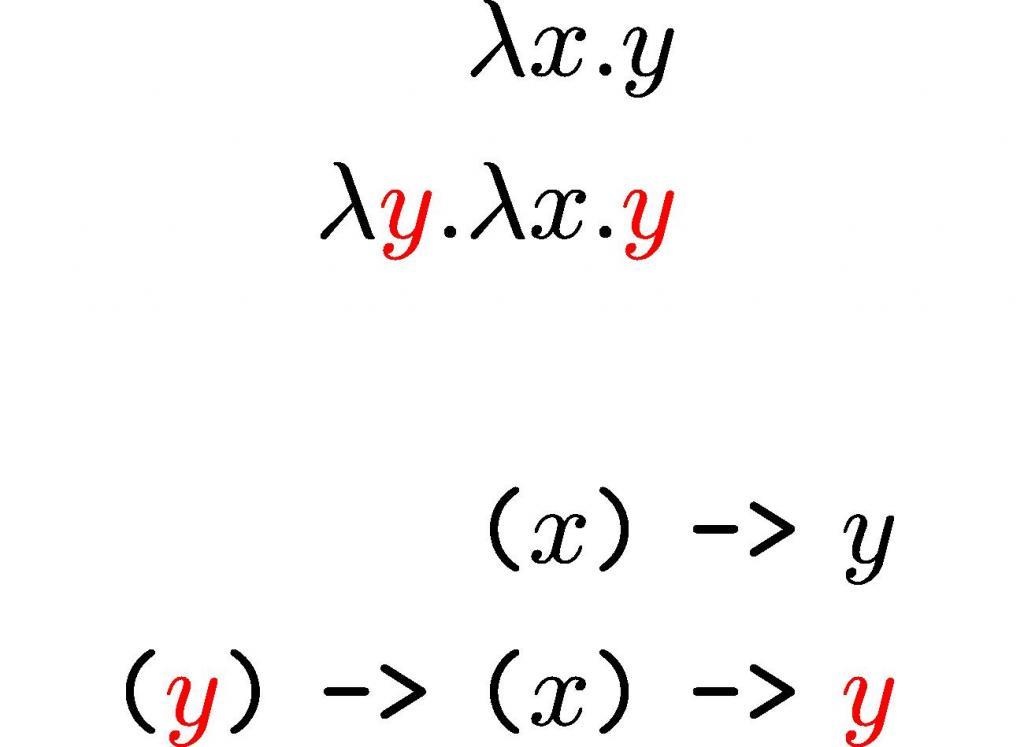Что означает лямбда в физике
Удельная теплота плавления
Содержание
Рассматривая график плавления и отвердевания льда в прошлом уроке, мы выяснили, что во время процесса плавления температура льда не меняется. Температура продолжит расти только тогда, когда лед полностью перейдет в жидкость. То же самое мы наблюдали и при кристаллизации воды.
Но, когда лёд плавится, он все равно получает энергию. Ведь во время плавления мы не выключаем горелку — лёд получает какое-то количество теплоты от сгорающего в спиртовке (или другом нагревателе) топлива. Куда уходит эта энергия? Вы уже знаете закон сохранения энергии — энергия не может исчезнуть.
В данном уроке мы подробно рассмотрим, что происходит во время процесса плавления, как изменяется энергия и температура. Это позволит нам перейти к новому определению — удельной теплоте плавления.
Изменение внутренней энергии и температуры при плавлении
Так на что же уходит энергия, которую мы сообщаем телу, при плавлении?
Вы знаете, что в кристаллических твердых телах атомы (или молекулы) расположены в строгом порядке (рисунок 1). Они не двигаются так активно, как в газах или жидкостях. Тем не менее, они также находятся в тепловом движении — колеблются.
Взгляните еще раз на график плавления и отвердевания льда (рисунок 2).
Нагревание льда идет на участке AB. В это время увеличивается средняя скорость движения его молекул. Значит, возрастает и их средняя кинетическая энергия и температура. Размах колебаний атомов (или молекул) увеличивается.
Так происходит то того момента, пока нагреваемое тело не достигнет температуры плавления.
При температуре плавления нарушается порядок в расположении частиц в кристаллах.
Так вещество начинает переход из твердого состояния в жидкое.
Значит, энергия, которую получает тело после достижения температуры плавления, расходуется на разрушение кристаллической решетки. Поэтому температура тела не повышается — участок графика BC.
Изменение внутренней энергии и температуры при отвердевании
При отвердевании происходит обратное.
Средняя скорость движения молекул и их средняя кинетическая энергия в жидкости (расплавленном веществе) уменьшается при охлаждении. Этому соответствует участок графика DE на рисунке 2.
Теперь силы притяжения между молекулами могут удерживать их друг около друга. Расположение частиц становится упорядоченным — образуется кристалл (участок графика EF).
Куда расходуется энергия, которая выделяется при кристаллизации? Температура тела остается постоянной во время этого процесса. Значит, энергия расходуется на поддержание этой температуры, пока тело полностью не отвердеет.
Теперь мы можем сказать, что
При температуре плавления внутренняя энергия вещества в жидком состоянии больше внутренней энергии такой же массы вещества в твёрдом состоянии.
Эта избыточная энергия выделяется при кристаллизации и поддерживает температуру тела на одном уровне во время всего процесса отвердевания.
Удельная теплота плавления
Опытным путем доказано, что для превращения твердых кристаллических тел одинаковой массы в жидкость необходимо разное количество теплоты. Тела при этом рассматриваются при их температурах плавления.
Удельная теплота плавления некоторых веществ
В таблице 1 представлены экспериментально полученные величины удельной теплоты плавления для некоторых веществ.
| Вещество | $\lambda, \frac<Дж><кг>$ | Вещество | $\lambda, \frac<Дж><кг>$ |
| Алюминий | $8.9 \cdot 10^5$ | Сталь | $0.84 \cdot 10^5$ |
| Лёд | $3.4 \cdot 10^5$ | Золото | $0.67 \cdot 10^5$ |
| Железо | $2.7 \cdot 10^5$ | Водород | $0.59 \cdot 10^5$ |
| Медь | $2.1 \cdot 10^5$ | Олово | $0.59 \cdot 10^5$ |
| Парафин | $1.5 \cdot 10^5$ | Свинец | $0.25 \cdot 10^5$ |
| Спирт | $1.1 \cdot 10^5$ | Кислород | $0.14 \cdot 10^5$ |
| Серебро | $0.87 \cdot 10^5$ | Ртуть | $0.12 \cdot 10^5$ |
Таблица 1. Удельная теплота плавления некоторых веществ (при нормальном атмосферном давлении)
Опытным путём доказано, что
при отвердевании кристаллического вещества выделяется точно такое же количество теплоты, которое поглощается при его плавлении.
Расчет количества теплоты, необходимого для плавления или отвердевания вещества
Количество теплоты, которое выделится при отвердевании, рассчитывается по этой же формуле. Но при этом необходимо помнить, что внутренняя энергия тела будет уменьшаться.
Примеры задач
Дано:
$m = 2 \space кг$
$t_1 = 0 \degree C$
$t_2 = 100 \degree C$
$\lambda = 3.4 \cdot 10^5 \frac<Дж><кг>$
$с = 4.2 \cdot 10^3 \frac<Дж><кг \cdot \degree C>$
Посмотреть решение и ответ
Решение:
Тогда, для превращения куска льда в кипяток нам потребуется количество теплоты:
$Q = Q_1 + Q_2 = 6.8 \cdot 10^5 \space Дж + 8.4 \cdot 10^5 \space Дж = 15.2 \cdot 10^5 \space Дж$.
Дано:
$m = 10 \space кг$
$t_1 = 29 \degree C$
$t_2 = 1539 \degree C$
$c = 460 \frac<Дж><кг \cdot \degree C>$
$\lambda = 2.7 \cdot 10^5 \frac<Дж><кг>$
Посмотреть решение и ответ
Решение:
$Q_1 = cm(t_2 — t_1)$.
$Q_1 = 460 \frac<Дж> <кг \cdot \degree C>\cdot 10 \space кг \cdot (1539 \degree C — 19 \degree C) = 4600 \frac<Дж> <\degree C>\cdot 1510 \degree C = 6 \space 946 \space 000 \space Дж \approx 69 \cdot 10^5 \space Дж$.
$Q_2 = \lambda m$.
$Q_2 = 2.7 \cdot 10^5 \frac<Дж> <кг>\cdot 10 \space кг = 27 \cdot 10^5 \space Дж$.
$Q = Q_1 + Q_2 = 69 \cdot 10^5 \space Дж + 27 \cdot 10^5 \space Дж = 96 \cdot 10^5 \space Дж$.
Дано:
$m_1 = 3 \space кг$
$\lambda_1 = 3.4 \cdot 10^5 \frac<Дж><кг>$
$c_2 = 500 \frac<Дж><кг \cdot \degree C>$
$t_1 = 800 \degree C$
$t_2 = 0 \degree C$
Посмотреть решение и ответ
Решение:
Лямбда-исчисление: описание теоремы, особенности, примеры
Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.
Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.
Пояснения и приложения

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.
Лямбда-исчисление может быть нетипизировано или напечатано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.
Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.
Для чайников
Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.
В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.
Происхождение символа
Лямбда не обозначает слово или аббревиатуру, она возникла, благодаря ссылки в «Принципиальной математике» Рассела, за которой следуют два типографских изменения. Пример обозначения: для функции f с f (y) = 2y + 1 равно 2ŷ + 1. И здесь используется символ каретки («шляпа») над y для пометки входной переменной.
Церковь изначально намеревалась использовать аналогичные символы, но наборщики не смогли разместить символ «шляпа» над буквами. Поэтому вместо этого они напечатали его изначально как «/y.2y+1». В следующем эпизоде редактирования наборщики заменили «/ » на визуально похожий символ.
Введение в лямбда исчисление
Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.
Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.
Лямбда-термины
Синтаксис исчисления определяет некоторые выражения как допустимые, а другие — как недействительные. Также, как различные строки символов являются допустимыми программами на Си, а какие-то — нет. Действительное выражение лямбда-исчисления называется «лямбда-термином».
Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:
Переменная x сама по себе является действительным лямбда-термином:
Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.
Определение

Лямбда-выражения состоят из:
Множество Λ, может быть определено индуктивно:
Обозначение
Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:
Свободные и связанные переменные
Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.
Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:
Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.
Сокращение
Значение лямбда-выражений определяется тем, как они могут быть сокращены.
Существует три вида урезания:
Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.
Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:
(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].
Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.
α-преобразование
Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.
Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.
Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.
В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.
В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.
Замена
y [x: = N] ≡ y, если x ≠ y
(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])
(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).
Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.
β-редукция
Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ‘) является Е [V: = Е’].
Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.
Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.
η-преобразование
Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.
Нормальные формы и слияние
Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.
Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).
Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.
Дополнительные методы программирования
Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.
Именованные константы
В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,
Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.
Объединяя в цепочку такие определения, можно написать «программу» лямбда-исчисления как ноль или более дефиниций функций, за которыми следует один лямбда-член, используя те определения, которые составляют основную часть программы.
Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.
Печатные аналоги
Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.
Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.
Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.