Что означает маленькая r в алгебре
СОДЕРЖАНИЕ
Основные определения
В этом разделе мы дадим некоторые определения ранга матрицы. Возможны многие определения; см. Альтернативные определения некоторых из них.
Считается, что матрица имеет полный ранг, если ее ранг равен максимально возможному для матрицы той же размерности, которая является меньшим из числа строк и столбцов. Матрица называется дефектной, если она не имеет полного ранга. Оценка дефицита матрицы представляет собой разность между наименьшим из числа строк и столбцов, и ранга.
Примеры
имеет ранг 1: есть ненулевые столбцы, поэтому ранг положительный, но любая пара столбцов линейно зависима. Точно так же транспонирование
Вычисление ранга матрицы
Ранг из форм эшелона строк
Например, матрица A, заданная формулой
может быть приведен в сокращенную форму строки-эшелона, используя следующие элементарные операции со строками:
. \ end <выровнено>>>
Конечная матрица (в форме эшелона строк) имеет две ненулевые строки, и, следовательно, ранг матрицы A равен 2.
Вычисление
При применении к вычислениям с плавающей запятой на компьютерах базовое исключение Гаусса ( разложение LU ) может быть ненадежным, и вместо этого следует использовать разложение с выявлением ранга. Эффективной альтернативой является разложение по сингулярным значениям (SVD), но есть и другие менее дорогостоящие варианты, такие как QR-разложение с поворотом (так называемая QR-факторизация с выявлением ранга ), которые по-прежнему более устойчивы в числовом отношении, чем исключение по Гауссу. Для численного определения ранга требуется критерий для принятия решения о том, когда значение, такое как сингулярное значение из SVD, следует рассматривать как ноль, практический выбор, который зависит как от матрицы, так и от приложения.
Доказательства того, что ранг столбца = ранг строки
Доказательство с использованием линейных комбинаций
Доказательство с использованием ортогональности
Альтернативные определения
Рейтинг с точки зрения недействительности
Рейтинг по сингулярным значениям
Характеристики
Приложения
В области коммуникационной сложности ранг коммуникационной матрицы функции дает границы объема коммуникации, необходимой двум сторонам для вычисления функции.
Обобщение
Матрицы как тензоры
Тензорный ранг матрицы также может означать минимальное количество простых тензоров, необходимых для выражения матрицы как линейной комбинации, и что это определение действительно согласуется с рангом матрицы, как здесь обсуждается.
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
Введение в R: линейная алгебра
R — очень мощный язык, разработанный специально для анализа и визуализации данных и машинного обучения, что делает его обязательным к изучению для любого начинающего специалиста по данным.
R особенно удобен для линейной алгебры. Встроенные типы данных, такие как векторы и матрицы, хорошо сочетаются со встроенными функциями, такими как алгоритмы решения собственных значений и определителей, а также с возможностями динамического индексирования.
В этой вводной в статье про R рассмотрим следующие реализации линейной алгебры:
Векторы
Массивы и матрицы
Векторы
Присваивание векторов
Также можно использовать функцию assign() :
Векторы можно свободно перемножать и дополнять константами:
Заметьте, что эта операция верна, даже когда x и y имеют разную длину. В данном случае R просто будет повторять x (иногда дробно), пока не достигнет длины y. Поскольку y равен 9 числам в длину, а x — 4, x повторится 2.25 раз пока не совпадёт с длиной y.
mean(x) вычисляет выборочное среднее, var(x) возвращает выборочную дисперсию, sort(x) возвращает вектор того же размера, что и x, элементы в котором расположены в порядке возрастания.
Генерация последовательностей
30:1 используется для генерации последовательности в обратном направлении.
Аналогичная функция rep() копирует объект различными способами. Например, rep(x, times=5) вернёт пять копий x впритык.
Логические векторы
Пропущенные значения
Индексирование векторов
Второй метод осуществляется с вектором положительных целых значений. В этом случае значения должны быть в наборе <1, 2, …, length(x)>. Для формирования результата соответствующие элементы вектора выбираются и объединяются в этом порядке. Важно помнить, что, в отличие от других языков, в R первый индекс равен 1, а не 0.
Преимущество этого подхода в том, что иногда буквенно-цифровые имена запомнить легче, чем индексы.
Другой пример: y[y аналогичен y — код просто заменяет все значения меньше 0 на отрицательные значения.
Массивы и матрицы
Массивы
Массив — это проиндексированный набор записей данных, не обязательно численный.
Вектор размерности — это вектор неотрицательных чисел. Если длина равна k, тогда массив k-размерный. Размерности индексируются от единицы вверх до значения, указанного вектором размерности.
Индексирование массивов
На индивидуальные элементы массива можно ссылаться, указав имя массива и в квадратных скобках индексы, разделённые запятыми.
Индексирование матриц
Массивы определяются вектором значений и размерностью матрицы. Значения вычисляются сначала сверху вниз, затем слева направо.
array(1:4, dim = c(2,2)) вернёт
В матрицах индексов запрещены отрицательные индексы, а значения NA и ноль разрешены.
Внешнее произведение двух матриц
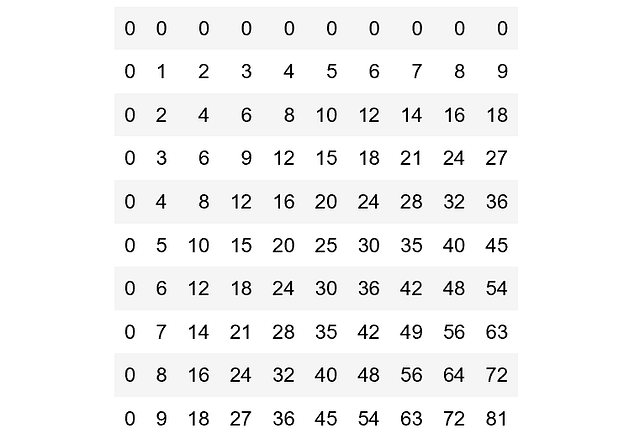
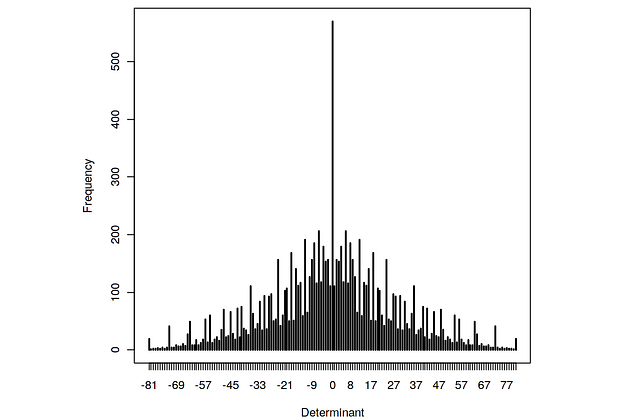
Демонстрация всех возможных определителей одноразрядных матриц 2×2
Рассмотрим определители матриц 2 на 2 [a, b; c, d], где каждая запись представляет собой неотрицательное число от 0 до 9. Задача: найти определители всех возможных матриц этой формы и отобразить на графике высокой плотности частоту, с которой встречается значение.
Или, перефразируя, нужно найти распределение вероятности определителя, если каждая цифра выбирается независимо и равномерно случайным образом.
Один из умных способов сделать это — использовать внешнюю функцию дважды.
Первая строка присваивает d этой матрице:
Вторая строка снова использует внешнюю функцию для расчёта всех возможных определителей. Последняя строка строит график.
Обобщённое транспонирование массива
Проще понять, если думать об этом как об обобщённом транспонировании матриц. Если A — это матрица, тогда B — просто результат перестановки матрицы A :
Умножение матриц
Если x — вектор, тогда x %*% A %*% x — его квадратичная форма.
Линейные уравнения и инверсия
Решение линейных уравнений является инверсией умножения матриц. Если
Собственные значения и собственные векторы
Для больших матриц лучше избегать вычисления собственных векторов, если они не нужны, используя выражение:
Сингулярное разложение и определители
Выравнивание методом наименьших квадратов и QR-разложение
Функция lsfit() возвращает список заданных результатов процедуры выравнивания методом наименьших квадратов. Присваивание наподобие этого:
выдаёт результаты выравнивания методом наименьших квадратов, где y — это вектор наблюдений, а X — проектная матрица.
ls.diag() используется для диагностики регрессии.
Тесно связанной функцией является qr().
Формирование блочных матриц
cbind() формирует матрицы, связывая матрицы горизонтально (поколоночно), а rbind() связывает матрицы вертикально (построчно).
В присвоении X аргументами cbind() должны быть либо векторы любой длины, либо столбцы одинакового размера (одинаковым количеством строк).
rbind() выполняет соответствующую операцию для строк.
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8