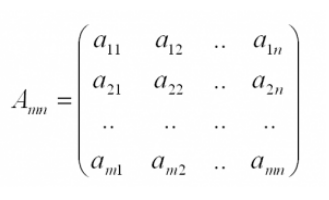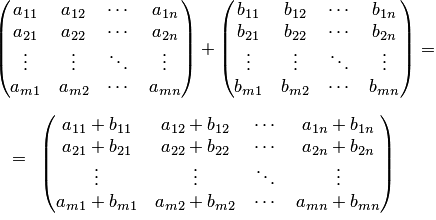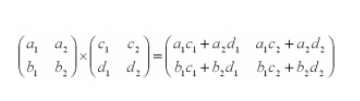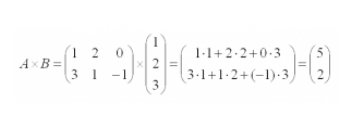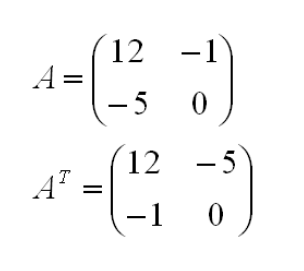Что означает матрица в математике
Что такое матрицы, откуда они взялись, и чем они полезны?
Первые упоминания о матрицах или «волшебных квадратах», как их тогда называли, были найдены на территории еще Древнего Китая, однако бум случился намного позже, в середине XVIII века, когда знаменитый математик Габриэль Крамер опубликовал свой труд под названием «Введение в анализ алгебраических кривых», в котором описывался алгоритм решения систем линейных уравнений совершенно новым методом.
Как следствие, в дальнейшем появляются «классический» метод решения Карла Фридриха Гаусса, теорема Гамильтона-Кели, работы Карла Вейерштрасса, Георга Фробениуса и других выдающихся ученых.
Занимательно, что только после всех этих открытий, а именно в 1850 году был непосредственно введен термин матрица, автором которого стал Джеймс Джозеф Сильвестр.
Сегодня термин «матрица» применяется во множестве разных областей: от программирования до кинематографии (здесь должно быть название фильма, о котором вы все подумали).
Матрица в математике – это таблица чисел, состоящая из определенного количества строк (m) и столбцов (n).
Вы встречаетесь с ними каждый день, так как любая числовая информация, занесенная в таблицу, уже в какой-то степени считается матрицей.
Примером могут служить:
● список телефонных номеров;
● различные статистические данные;
● табель успеваемости ученика и многое другое.
Сами матрицы всегда обозначаются прописными латинскими буквами (A, B, C…), а элементы матрицы – строчными (a, b, c…). Индексы обозначают местоположение элемента матрицы в системе, причем первое число – это всегда номер строки, а второе – это всегда номер столбца. Например, а23 находится во второй строке и в третьем столбце, а31 в третьей строке и первом столбце и т.д.
Важно произносить элементы матриц правильно, так а23 будет звучать как «а два три», а не «а двадцать три».
Примеры записи матриц
Для чего нужны матрицы
Теперь выясним, для чего нам так нужны матрицы конкретно в математике?
В качестве примера рассмотрим простейшую систему двух линейных уравнений и решим ее методом сложения, который изучают в школьном курсе.
Оказывается, можно решить эту систему уравнений альтернативным способом, используя матрицы, и называется он метод Крамера.
Вы можете подумать, зачем усложнять решение какими-то матрицами?
В данном случае да, при желании можно эту систему и в уме решить. Но представьте себе систему, состоящую хотя бы из 5 линейных уравнений с пятью неизвестными. А если система состоит из 6, 7 или ещё больше уравнений? Решать её школьным методом, мягко говоря, трудоёмко. Зато применяя тот же метод Крамера, решение будет выглядеть достаточно компактно.
Система с тремя уравнениями
В подтверждение вышесказанного рассмотрим систему уравнений с тремя неизвестными и решим её метод Крамера.
Из этого следует, что матрицы – еще один способ решения систем линейных алгебраических уравнений (СЛАУ).
На основе второго примера убеждаемся в том, что матрицы могут применяться в тех случаях, когда применение школьных методов решения СЛАУ не является рациональным.
На самом деле за прошедшие столетия алгебра матриц изучена более, чем достаточно, и тот факт, что матрицы используются повсеместно однозначно подтверждает необходимость их изучения.
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Матрица (математика)
Из Википедии — свободной энциклопедии
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.
Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n; и обратно — каждой квадратной матрице порядка n может быть сопоставлен единственный линейный оператор, действующий в этом пространстве. [2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.
То же можно сказать о представлении матрицами билинейных (квадратичных) форм.
В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.
От действий над матрицами к пониманию их сути…
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.
Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».
Что такое матрица: как складывать и умножать матрицы, чтобы не запутаться
Представьте: сидите на паре, погрязнув в огромных формулах, нить рассуждений потеряна, и вы уже не понимаете, о чем идет речь. Знакомое ощущение? Вот именно. Чтобы вы не упускали самую суть вещей, мы подготовили объяснение некоторых непростых тем простыми словами.
А чтобы вообще всегда были в курсе событий, подписывайтесь на наш телеграм-канал.
Что такое матрицы
Сегодня поговорим о матрицах. Пройти через эту тему предстоит, наверное, всем студентам, изучающим высшую математику (линейную алгебру, точнее говоря).
Именно с матриц начинается большинство курсов высшей математики. И пусть вас не пугает слово высшая. На самом деле, все не так страшно. Смотрите сами.
Матрица – это таблица. Таблица чисел, или букв, за которыми скрываются числа.
Матрицы могут быть разного размера: квадратные, прямоугольные, есть матрицы, состоящие всего из одной строки или одного столбца (горизонтальные и вертикальные).
Размер матрицы определяется количеством строк m и столбцов n. Номера строк и столбцов – буквами i и j соответственно.
А теперь, что еще нужно в первую очередь знать о работе с матрицами.
Как складывать матрицы
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера.
Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример.
Вычитание выполняется по аналогии, только вместо плюса пишем минус.
Как умножать матрицы
Во-первых, запомните: матрицу А можно умножить на матрицу B, только если если число столбцов матрицы А равно числу строк матрицы В.
При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м.
Вместо букв в матрице могут стоять реальные числа. Вот что получится, если умножить такие матрицы:
Можно и просто умножить матрицу на число. Для этого каждый ее элемент умножается на это число.
Что такое транспонированная матрица
Транспонировать матрицу – значит поменять строки и столбцы местами.
Вот как будет выглядеть матрица из самого первого примера, если ее транспонировать. Сама операция транспонирования обозначается индексом Т.
Что такое детерминант матрицы
Детерминант – это определитель – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко. А если часто, то с этим справятся специалисты студенческого сервиса. Обращайтесь, они помогут!
Анастасия Бабина. В моей фамилии часто ставят ударение на «И», но я привыкла. Копирайтер и редактор компании Zaochnik. Любительница мистических триллеров, отчаянный киноман и гурман в хорошей форме.