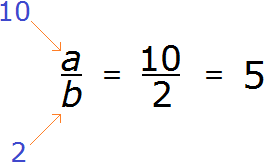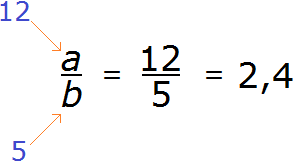Что означает множество натуральных чисел

Что такое множество?

Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.

В математике множество рассматривается намного шире. Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Обозначим множество наших друзей через заглавную латинскую букву F ( friends ), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

Читается как «2 принадлежит множеству делителей числа 6»

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

Зададим множество, которое состоит из одного числа 2

Зададим множество, которое состоит из двух чисел: 2 и 5

Множество натуральных чисел

Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.

Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.

В математике множество натуральных чисел обозначается заглавной латинской буквой N.

Например, укажем, что число 1 принадлежит множеству натуральных чисел. Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N

Читается как: «единица принадлежит множеству натуральных чисел»

Множество целых чисел

Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.

Укажем, к примеру, что число −5 принадлежит множеству целых чисел:

Укажем, что 10 принадлежит множеству целых чисел:

Укажем, что 0 принадлежит множеству целых чисел:

В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.

Множество рациональных чисел

Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.

В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).

Например, представим, что вместо a стоит число 10, а вместо b — число 2

10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби 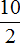, а значит число 5 входит во множество рациональных чисел.

Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.

Теперь представим, что вместо a стоит число 12, а вместо b — число 5.

12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби 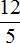, а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.

Мы вычислили дробь 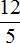и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:

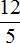
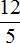
При выделении целой части в дроби , получается смешанное число . Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.

В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:

Множество рациональных чисел обозначается заглавной латинской буквой Q.

Например укажем, что дробь принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:

∈ Q

Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:

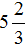
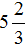
Укажем, что смешанное число принадлежит множеству рациональных чисел:

∈ Q

Вводный урок по множествам завершён. В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

12 thoughts on “Что такое множество?”

Источник

Обозначение, запись и изображение числовых множеств

Из большого количества разнообразных множеств особо интересными и важными являются числовые множества, т.е. те множества, элементами которых служат числа. Очевидно, что для работы с числовыми множествами необходимо иметь навык записи их, а также изображения их на координатной прямой.

Запись числовых множеств

N – множество всех натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; J – множество иррациональных чисел; R – множество действительных чисел; C – множество комплексных чисел.

Напомним также следующие обозначения:

Рассмотрим теперь схему описания числовых множеств на примере основных стандартных случаев, наиболее часто используемых на практике.

Таким же образом, объединяя различные числовые промежутки и множества отдельных чисел, возможно дать описание любому числовому множеству, состоящему из действительных чисел. На основе сказанного становится понятно, для чего вводятся различные виды числовых промежутков, такие как интервал, полуинтервал, отрезок, открытый числовой луч и числовой луч. Все эти виды промежутков совместно с обозначениями множеств отдельных чисел дают возможность через их объединение описать любое числовое множество.

Изображение числовых множеств на координатной прямой

В практических примерах удобно использовать геометрическое толкование числовых множеств – их изображение на координатной прямой. К примеру, такой способ поможет при решении неравенств, в которых нужно учесть ОДЗ – когда нужно отобразить числовые множества, чтобы определить их объединение и/или пересечение.

Зачастую и не указывают начало отсчета и единичный отрезок:

В большинстве случаев возможно не соблюдать абсолютную точность чертежа: вполне достаточно схематичного изображения без соблюдения масштаба, но с сохранением взаимного расположения точек относительно друг друга, т.е. любая точка с бОльшей координатой должна быть правее точки с меньшей. С учётом сказанного уже имеющийся чертеж может выглядеть так:

Отдельно из возможных числовых множеств выделяют числовые промежутки интервалы, полуинтервалы, лучи и пр.)

Информация, приведенная в данной статье, призвана помочь получить навык видеть запись и изображение числовых множеств так же легко, как и отдельных числовых промежутков. В идеале записанное числовое множество сразу должно представляться в виде геометрического образа на координатной прямой. И наоборот: по изображению должно с легкостью формироваться соответствующее числовое множество через объединение числовых промежутков и множеств, являющихся отдельными числами.

Источник

Множества натуральных и целых чисел

Понятие и свойства натуральных чисел

Натуральные числа – множество чисел, используемых для счёта предметов.

В отечественной литературе используются следующие обозначения:

N = <1,2,3,…>— натуральные числа без нуля

$N_0 = Z_+$ = <0,1,2,3,…>— расширенное множество с нулём

В зарубежной литературе по стандарту ISO 80000-2 (2009 год):

$N^* =$ <1,2,3,…>— натуральные числа без нуля

N = <0,1,2,3,…>— расширенное множество с нулём

Свойства натуральных чисел

1. 1 – первое натуральное число, перед ним нет никаких натуральных чисел.

2. За каждым натуральным числом идёт следующее натуральное число, причём единственное.

4. Множество натуральных чисел бесконечно.

5. Для натуральных чисел справедлива аксиома индукции Пеано.

Замкнутые операции над натуральными числами

Незамкнутые операции над натуральными числами (не всегда результаты будут натуральными)

Понятие и свойства целых чисел

Целые числа – расширение множества целых чисел, получаемое при добавлении к нему нуля и отрицательных чисел.

Множество целых чисел обозначается Z.

Свойства целых чисел

1. Множество целых чисел бесконечно.

2. На множестве определено отношение порядка

4. Для каждого целого числа a существует противоположное ему число –a, при этом a+(-a) = 0.

Замкнутые операции над целыми числами

Таким образом, расширение множества натуральных чисел до целых чисел «замыкает» множество по операциям вычитания и деления нацело. В алгебре говорят, что множество целых чисел образует «кольцо».

Примеры

Результатом деления является натуральное число. Что и требовалось доказать.

Запишем систему уравнений:

Получается, что a и b всегда существуют и являются натуральными, т.к. произведение двух последовательных натуральных чисел всегда делится на 2 нацело (ведь одно из этих чисел обязательно будет чётным). Что и требовалось доказать.

Примеры разложений по полученной формуле:

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

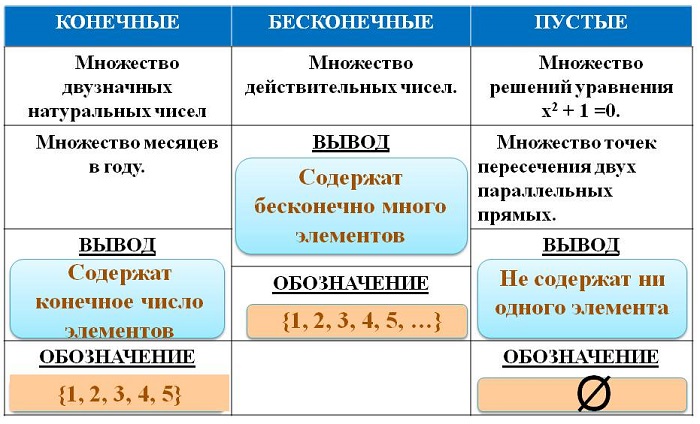
Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

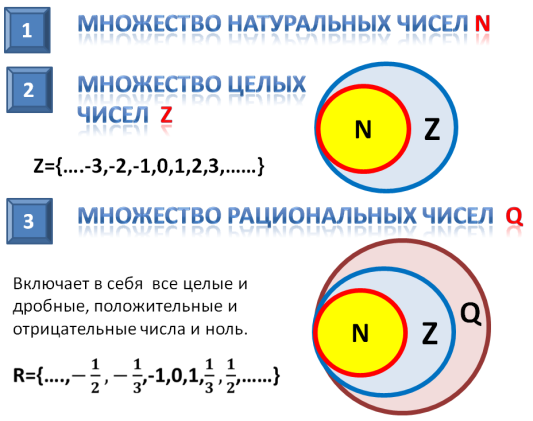
Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

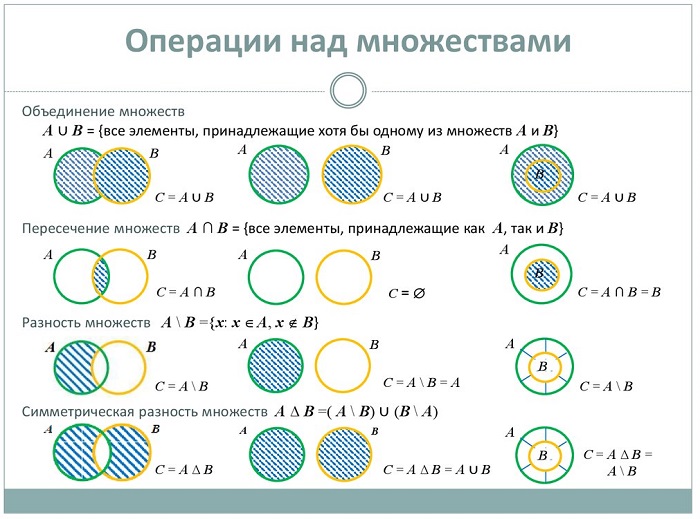
Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

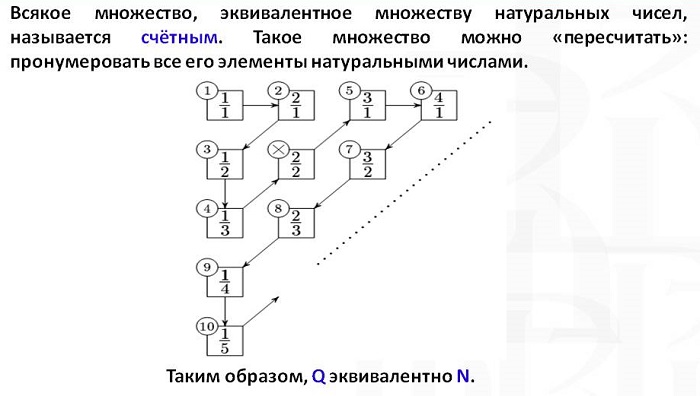
Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник

Репетитор по математике

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Источник