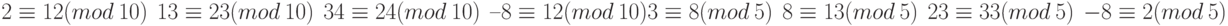Что означает mod в математике
Что означает mod в математике
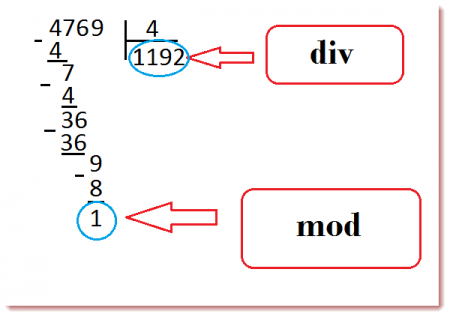
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
Mod и остаток — не одно и то же
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Вот где мы попадаем в странную серую область.
Математика циферблата
Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
JavaScript с этим согласен:
Google согласен с первым утверждением, но не согласен со вторым:
Ruby согласен с Google:
Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:
Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
Деление чисел с остатком
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Тогда необходимо взять q такое, чтобы данное неравенством b * q
Модульная арифметика
2.2. Модульная арифметика
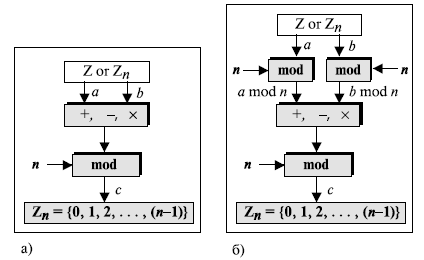
Операции по модулю
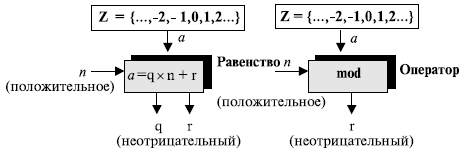
Как показано на рис. 2.9, оператор по модулю ( mod ) выбирает целое число ( a ) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ).
Мы можем сказать, что
Найти результат следующих операций:
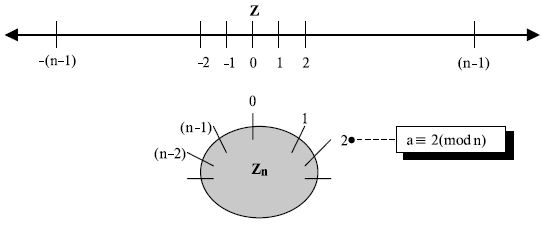
Система вычетов: Zn
Сравнения
Рисунок 2.11 показывает принцип сравнения. Мы должны объяснить несколько положений.
Система вычетов
Круговая система обозначений
Операции в Zn
Выполните следующие операторы (поступающие от Zn ):
а. Сложение 7 и 14 в Z15
б. Вычитание 11 из 7 в Z13
в. Умножение 11 на 7 в Z20
Ниже показаны два шага для каждой операции:
Выполните следующие операции (поступающие от Zn ):
a. Сложение 17 и 27 в Z14
b. Вычитание 43 из 12 в Z13
Ниже показаны два шага для каждой операции:
Свойства
Первое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n
Третье свойство: (a x b) mod n = [(a mod n) x (b mod n)] mod n
Рисунок 2.14 показывает процесс до и после применения указанных выше свойств. Хотя по рисунку видно, что процесс с применением этих свойств более длинен, мы должны помнить, что в криптографии мы имеем дело с очень большими целыми числами. Например, если мы умножаем очень большое целое число на другое очень большое целое число, которое настолько большое, что не может быть записано в компьютере, то применение вышеупомянутых свойств позволяет уменьшить первые два операнда прежде, чем начать умножение. Другими словами, перечисленные свойства позволяют нам работать с меньшими числами. Этот факт станет понятнее при обсуждении экспоненциальных операций в последующих лекциях.
Следующие примеры показывают приложение вышеупомянутых свойств.
Сравнение чисел по модулю
Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
1 ) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
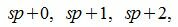 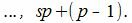 |
Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
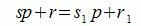 |
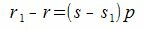 | (2) |
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
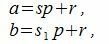 |
где s и s1 некоторые целые числа.
Разность этих чисел
 | (3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
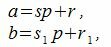 |
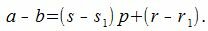 |
По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1. p−1, то абсолютное значение |r−r1| Свойство 1. Для любого a и p всегда
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
| a≡b mod (p) и m≡n mod (p), |
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
| a≡b mod (p) и m≡n mod (p), |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| . |
| a k ≡b k mod (p). |
Все свойства 1-5 представить в следующем утверждении:
При делении все обстоит иначе. Из сравнения
не всегда следует сравнение
Утверждение 5. Пусть
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
Так как m(a−b) делится на k, то
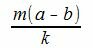 |
имеет нулевой остаток. Тогда
 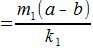 . . |
 |
имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
и m является один из делителей числа p, то
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.