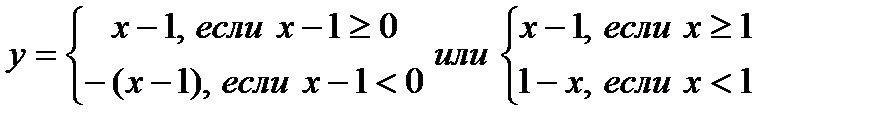Что означает модуль в функции
Построение графиков с модулем
путём преобразований
Модуль аргумента и модуль функции
Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.
В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.
Пример 1.
Пример 2.
Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.
III При построении из графика функции y = f(x) более сложных графиков, например, вида y = k·f (a|x| + b) + c или y = k·|f (ax + b)| + c тщательно соблюдайте последовательность преобразований.
Пример 3.
Заметим, что x 2 = |x| 2 (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду |y| = (|x| − 1) 2 − 6 и строим её график последовательными преобразованиями.
Строим график функции f(x) = (x − 1) 2 − 6 переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции f(|x|) = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению |y| = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Ox.
- 1.
 2.
2. 3.
3. 4.
4.
5.
 6.
6.
| 1.y = x 2 | 2.y = (x − 1) 2 | 3.y = (x − 1) 2 − 6 | 4.y = (|x| − 1) 2 − 6 |
| 5.y = (|x| − 1) 2 − 6, y ≥ 0 | 6.|y| = (|x| − 1) 2 − 6 |
Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.
Пример 4.
Сумма модулей
Если формула функции включает сумму или разность несколько модулей, то следует разбить координатную плоскость на участки и построить каждую ветвь графика отдельно. Границы участков определяются приравниванием каждого модуля к нулю и решением соответствующего уравнения. Подробный пример такого подхода можно увидеть в задаче 1 на странице, посвященной решению уравнений с параметрами.
Однако, если подмодульные выражения простые и содержат элементарные функции, графики которых вам хорошо известны, то можно получить результат прямым сложением ординат этих графиков в характерных точках.
Пример 5.
Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
Теперь проверьте себя.
Пример 6.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Свойство модуля. Построение графика функции «Модуль». Свойства функции



Если рассматривать геометрический смысл модуля, то говорят, что модуль – расстояние до конкретной точки координатной прямой от начала координат в единичных отрезках. Так как никакое расстояние не может быть отрицательным, то легко понять, что значение модуля любого числа – это число неотрицательное. Например, расстояние от начала координат до точки А(-5) равно 5. По-другому, |-5|=5.
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчёта, т.е. удалена от начала координат на 0 единичных отрезков. Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули: |-а|=|а|.
Итак, 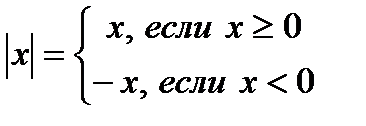
Свойства модулей чисел: 1) |а|≥0; 2) |ab|=|a|⸳|b|; 3) 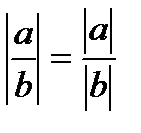
Решим уравнение |x-1|=2, используя определение и смысл модуля.
|-2|=2 и |2|=2. Т.е. х-1= –2 или х-1=2. Получили 2 линейных уравнения. Корнем уравнения х-1= –2 является число х= –1, а корнем уравнения х-1=2 является число х=3.
Проверим решения. |-1-1|=|-2|=2, |3-1|=|2|=2.
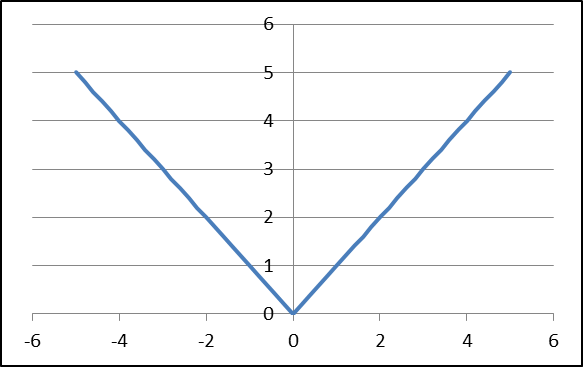
Перейдём к построению графика функции у= |х|. Вспомним алгоритм построения графика функции:
1) находим область определения функции;
2) берём несколько точек из области определения функции;
3) подставляем значения х из ООФ в уравнение функции;
4) полученные пары чисел (х;у) – точки графика функции.
Областью определения функции «Модуль» является вся числовая ось. Для построения графика возьмём 3 или 5 точек. 1 точка – вершина графика, 2 или 4 точки – для более точного построения.
| х | -2 | -1 | 0 | 1 | 2 |
| у | 2 | 1 | 0 | 1 | 2 |
Построим график функции у=|х-1|. Так как в формулу функции входит модуль, то его необходимо раскрыть, рассмотрев 2 случая. Поэтому функцию можно записать в виде
То есть при х≥1 строится луч, удовлетворяющий уравнению х-1, а при х
Рассмотрим неравенство |х|≤а, где а>0. Этому неравенству удовлетворяют все точки х, находящиеся на расстоянии, не большем а, от точки 0, т.е. точки отрезка [-a;a].